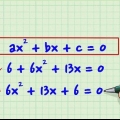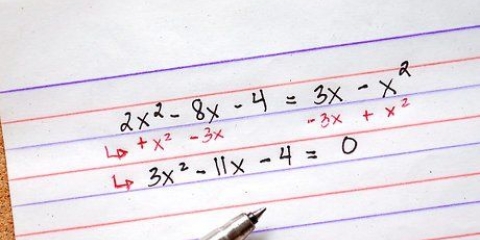Vid (x + 3x) ser vi att x är lika. Vid (-6x - 18) ser vi att -6 är lika. 
Genom att faktorisera x får vi x(x + 3). Genom att dekomponera -6 från den andra biten får vi -6(x + 3). 
Detta ger (x + 3)(x - 6). 
Lösningarna är -3 och √6. 

Faktorer är de tal som du kan multiplicera tillsammans för att få ett annat tal. I det här fallet är dessa faktorerna 10, eller "d": 1, 2, 5 och 10. 
Börja med att använda den första faktorn, 1. ersättning "1" för varje "X" i jämförelsen:
(1) - 4(1) - 7(1) + 10 = 0 Detta ger: 1 - 4 - 7 + 10 = 0. Eftersom 0 = 0 är ett sant påstående vet du att x = 1 är lösningen. 
"x = 1" är det samma som "x - 1 = 0" eller "(x - 1)". Du har bara en "1" subtraherad från varje sida av ekvationen. 
Kan du faktorisera (x - 1) från x? Nej det är inte möjligt. Men om du först lånar a -x från den andra variabeln: x(x - 1) = x - x. Kan du faktorisera (x - 1) från vad som återstår av den andra variabeln? Nej, det är inte möjligt här heller. Du måste låna något från den tredje variabeln igen, vilket är 3x av -7x. Detta ger oss -3x(x - 1) = -3x + 3x. Eftersom du tog 3x av -7x är den tredje variabeln nu -10x och konstanten är 10. Kan du lossa detta. Ja självklart! -10(x - 1) = -10x + 10. Vad du har gjort är att arrangera om variablerna så att du kan få faktorn (x - 1) från hela ekvationen. Den modifierade ekvationen ser ut så här: x - x - 3x + 3x - 10x + 10 = 0, men är fortfarande samma som x - 4x - 7x + 10 = 0. 
x(x - 1) - 3x(x - 1) - 10(x - 1) = 0. Du kan ordna om dessa för att göra det lättare att lösa upp igen: (x - 1)(x - 3x - 10) = 0. Här försöker du bara faktorisera (x - 3x - 10). Faktorerna blir då (x + 2)(x - 5). 
(x - 1)(x + 2)(x - 5) = 0 Detta ger lösningarna för 1, -2 och 5. Infoga -2 i ekvationen: (-2) - 4(-2) - 7(-2) + 10 = -8 - 16 + 14 + 10 = 0. Infoga 5 i ekvationen: (5) - 4(5) - 7(5) + 10 = 125 - 100 - 35 + 10 = 0.
Faktorering av ett tredjegradspolynom
Den här artikeln handlar om faktorisering av ett kubiskt polynom, även kallat polynom. Vi kommer att utforska hur vi kan göra detta genom att gruppera och använda faktorerna i den fria termen.
Steg
Del 1 av 2: Lös upp genom att gruppera

1. Dela upp polynomet i två grupper. Att dividera polynomet hjälper till att lösa varje enskild del.
- Anta att vi arbetar med följande polynom:" x + 3x - 6x - 18 = 0. Låt oss dela upp detta i (x + 3x) och (-6x - 18)

2. Försök ta reda på vad som är likadant i varje grupp.

3. Ta bort dessa lika faktorer från de två termerna.

4. Om var och en av de två termerna innehåller samma faktor kan du kombinera dessa faktorer.

5. Hitta lösningen genom att titta på rötterna. Om du har x i en kvadratrot, kom ihåg att både positiva och negativa tal är giltiga för den ekvationen.
Del 2 av 2: Factoring med friperioden

1. Ordna om uttrycket i följande form: axe+bx+cx+d.
- Anta att du arbetar med ekvationen: x - 4x - 7x + 10 = 0.

2. Hitta alla faktorer av "d". Konstanten "d" blir talet utan variabler bredvid "X".

3. Hitta en faktor som gör polynomet lika med noll. Vi vill bestämma vilken faktor som gör polynomet lika med noll om vi tillämpar denna faktor för "X" fyll i ekvationen.
(1) - 4(1) - 7(1) + 10 = 0

4. Gå nu och ordna om allt. Om x=1 så är det möjligt att skriva denna ekvation något annorlunda utan att ändra innebörden.

5. Faktorera ut kvadratroten ur ekvationen. "(x - 1)" är roten. Försök att ta bort dessa från resten av ekvationen. Gör detta med ett polynom i taget.

6. Fortsätt med att ersätta faktorerna för den fria perioden. Titta på siffrorna du löste med (x - 1) i steg 5:

7. Din lösning är de faktoriserade rötterna. Kontrollera denna lösning genom att infoga var och en av dem tillbaka i den ursprungliga ekvationen.
Tips
- Kubikekvationen är produkten av 3 förstagradsekvationer eller av en förstagradsekvation och en andragradsekvation som inte kan faktoriseras. I det senare fallet, efter att ha hittat förstagradspolynomet, använder du långdivision för att hitta andragradspolynomet.
- Det finns inga kubiska polynom som inte kan faktoriseras när det gäller reella tal, eftersom denna ekvation måste ha en kvadratrot ur reella tal. Tredjegradsekvationer som x + x + 1 som har en irrationell reell rot kan inte faktoriseras till polynom med heltal eller rationella tal som koefficient. Även om det kan inkluderas i själva ekvationen, kan det inte reduceras till ett heltalspolynom.
Metod 2 innebär lång division av två polynom, en.v:
(x-1) ∕x³ - 4x²-7x+10 ∕
- x³ - 1x².................................= (x-1) ( x²)
- - 3x²-7x
- 3x²+ 3x.........................= (x-1) (-3x)
- - 10x + 10
- 10x + 10................= (x-1) (-10)
- 0............................ x²- 3x-10 (kvot)
Bestämningarna x², -3x och -10 av kvoten erhålls genom att alltid subtrahera den första termen av divisorn ( x ) från den första termen av utdelningen, eller vad som är kvar av den ( x³, -3x², -10x ).
"Faktorering av ett tredjegradspolynom"
Оцените, пожалуйста статью