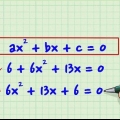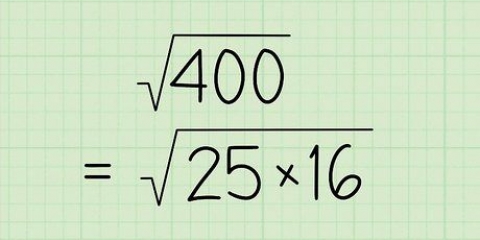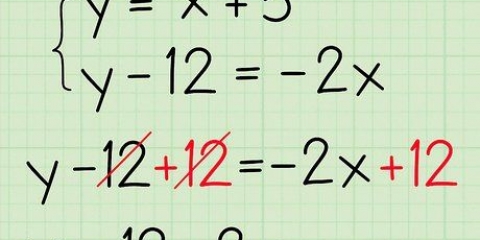→
→ 
 →
→ 
 →
→ 
Notera hur minustecknen förblir framför 2:an. När en term subtraheras, förblir minustecknet framför det. 
Övningsuppgift: .
. Faktorer av 3:1, 3 Faktorer av 6: 1, 2, 3, 6. `Den största gemensamma delaren är 3`. 
Övningsuppgift: .
. Hitta de största gemensamma divisorerna: 3 Så här tar du bort faktor från båda termerna:

Övningsuppgift:
Hitta de största gemensamma divisorerna: 3 Så här tar du bort faktor från båda termerna:
Multiplicera faktor med nytt uttryck:
Slutligt upplöst svar: 

För att ändra ordning på villkor:
Hitta den största gemensamma delaren:
Så här tar du bort faktor från båda termerna:
Multiplicera faktor med nytt uttryck:
Kolla svar:


Övningsuppgift:
Lika med noll:


Övningsuppgift:
Lika med noll:
Upplösa:

Övningsuppgift:
Lika med noll:
Upplösa:
Gör båda termerna lika med noll 0: 




y = 0 

y = 4 


 Detta svar är korrekt
Detta svar är korrekt

 Detta svar är också korrekt.
Detta svar är också korrekt.

Ursprunglig uppgift:
För att ändra ordning på villkor:
Så här slår du ihop liknande termer:
Hitta de största gemensamma divisorerna:
Upplösa:

Formeln för skillnaden mellan perfekta kvadrater:
Övningsuppgift:
Bestäm kvadratrötterna: 

Tillämpa kvadratrötter på formeln: 

Formel för skillnaden mellan tredje makter:
Övningsuppgift:
Bestäm kubrötter: ![Factoring binomialer {sqrt[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Factoring binomialer {sqrt[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)
Använd kuber på formeln: 

Formel för summan av perfekta kuber:
Övningsuppgift:
Bestäm kubrötter: ![Factoring binomialer {sqrt[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Factoring binomialer {sqrt[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)
Applicera kuberna på formeln: 
Factoring binomialer
I algebra är binomial tvåtermsuttryck kopplade med ett plus- eller minustecken, som t.ex 
Steg
Del 1 av 3: Factoring binomialer

1. Gå igenom grunderna för factoring igen. Factoring är att dela upp ett stort antal i sina enklaste delare. Var och en av dessa delar kallas en "faktor". Till exempel är talet 6 delbart med fyra olika tal: 1, 2, 3 och 6. Så 1, 2, 3 och 6 är faktorerna för 6.
- Faktorerna 32 är 1, 2, 4, 8, 16 och 32
- Både `1` och siffran du faktor är alltid faktorer. Så faktorerna för ett litet tal som 3 är bara 1 och 3.
- Faktorer är bara de siffror som är helt delbara, det vill säga "hela" talen. Du kan dividera 32 med 3,564 eller 21,4952, men det är inte faktorer, bara decimaltal.

2. Lista termerna för binomialen för att göra dem lättare att läsa. Ett binomial är inget annat än addition eller subtraktion av två termer, varav minst en innehåller en variabel. Ibland har dessa variabler exponenter, som t.ex  eller
eller  . Om du försöker faktorisera binomialer för första gången, hjälper det att ordna ekvationerna i fallande variabeltermer, vilket betyder att den största exponenten kommer sist. Till exempel:
. Om du försöker faktorisera binomialer för första gången, hjälper det att ordna ekvationerna i fallande variabeltermer, vilket betyder att den största exponenten kommer sist. Till exempel:
 eller
eller  . Om du försöker faktorisera binomialer för första gången, hjälper det att ordna ekvationerna i fallande variabeltermer, vilket betyder att den största exponenten kommer sist. Till exempel:
. Om du försöker faktorisera binomialer för första gången, hjälper det att ordna ekvationerna i fallande variabeltermer, vilket betyder att den största exponenten kommer sist. Till exempel: →
→ 
 →
→ 
 →
→ 

3. Hitta den största gemensamma delaren för båda termerna. Det betyder att du letar efter det största talet som båda delarna av binomialen är delbara med. Om detta inte fungerar, faktorisera båda siffrorna på egen hand och se vad det högsta matchande talet är. Till exempel:
 .
.
4. Dela den största gemensamma delaren för varje term. Om du känner till den gemensamma nämnaren måste du ta bort den från varje term. Observera att du bara delar upp termerna vilket gör var och en till ett mindre divisionsproblem. Om det görs på rätt sätt har båda ekvationerna samma faktor:
 .
.

5. Multiplicera din faktor med det resulterande uttrycket för att avrunda. I det sista problemet tog du bort en 3:a och du får  . Men du vill inte bli av med de 3 helt, bara inkludera dem för att förenkla saker och ting. Du kan inte bara ta bort nummer utan att lägga tillbaka dem! Multiplicera faktorn med uttrycket för att slutföra detta avsnitt. Till exempel:
. Men du vill inte bli av med de 3 helt, bara inkludera dem för att förenkla saker och ting. Du kan inte bara ta bort nummer utan att lägga tillbaka dem! Multiplicera faktorn med uttrycket för att slutföra detta avsnitt. Till exempel:
 . Men du vill inte bli av med de 3 helt, bara inkludera dem för att förenkla saker och ting. Du kan inte bara ta bort nummer utan att lägga tillbaka dem! Multiplicera faktorn med uttrycket för att slutföra detta avsnitt. Till exempel:
. Men du vill inte bli av med de 3 helt, bara inkludera dem för att förenkla saker och ting. Du kan inte bara ta bort nummer utan att lägga tillbaka dem! Multiplicera faktorn med uttrycket för att slutföra detta avsnitt. Till exempel:




6. Kontrollera ditt arbete genom att multiplicera till den ursprungliga ekvationen. Om du gjorde allt rätt är det lätt att kontrollera om du gjorde rätt. Multiplicera din faktor med båda individuella termer inom parentes. Om det stämmer överens med den ursprungliga givna binomialen, så har du gjort det bra. Från början till slut löser vi uttrycket  på att träna:
på att träna:
 på att träna:
på att träna:




Del 2 av 3: Factoring binomialer för att lösa ekvationer

1. Faktor för att förenkla ekvationer så att de är lättare att lösa. När man löser en ekvation med binomialer, särskilt komplexa binomialer, kan det verka som att det inte finns något sätt att få allt att matcha. Försök till exempel att lösa följande:  . Ett sätt att göra detta, särskilt med exponenter, är att först faktorisera.
. Ett sätt att göra detta, särskilt med exponenter, är att först faktorisera.
 . Ett sätt att göra detta, särskilt med exponenter, är att först faktorisera.
. Ett sätt att göra detta, särskilt med exponenter, är att först faktorisera. - Övningsuppgift:
- Kom ihåg att binomialer bara kan ha två termer. Om det finns fler än två terminer måste du lära sig lösa polynom.

2. Addera och subtrahera så att en sida av ekvationen är lika med noll. Hela denna strategi bygger på en av matematikens mest grundläggande fakta: något multiplicerat med noll måste vara lika med noll. Så om din ekvation är lika med noll, måste en av de faktoriserade termerna vara lika med noll! Till att börja med kommer du att addera och subtrahera så att en sida är lika med noll.




3. Lös upp sidan som inte är noll som du är van vid. Vid det här laget låtsas du bara att den andra sidan inte existerar. Hitta den största gemensamma delaren, dela den och skapa sedan ditt faktoriserade uttryck.




4. Sätt termerna inom och utanför parentesen lika med noll. I övningsuppgiften multiplicerar du 2y med (4 – y), och detta måste vara lika med noll. Eftersom något multiplicerat med noll är lika med noll betyder det att 2y eller (4 – y) måste vara lika med noll. Gör två separata ekvationer för att ta reda på vilket värde y måste ha för att göra endera sidan lika med noll.






5. Lös båda ekvationerna för noll för det slutliga svaret eller svaren. Du kan få ett eller flera svar. Kom ihåg att bara en sida måste vara lika med noll, så du kan få några olika värden för y som löser samma ekvation. De sista stegen i övningsuppgiften:





6. Tillämpa dina svar tillbaka till den ursprungliga ekvationen för att se till att de är korrekta. När du har hittat rätt värden för y bör du kunna använda dem för att lösa ekvationen. Detta är så enkelt som att prova varje värde på y istället för variabeln som visas nedan. Svaren är y = 0 och y = 4, så:


 Detta svar är korrekt
Detta svar är korrekt

 Detta svar är också korrekt.
Detta svar är också korrekt.Del 3 av 3: Att hantera tuffare problem

1. Kom ihåg att variabler räknas som faktorer, även med exponenter. Kom ihåg att factoring handlar om att bestämma vilka tal som passar in i heltal. Uttrycket  är ett annat sätt att säga
är ett annat sätt att säga  . Det betyder att du kan placera valfritt x utanför parentes om den andra termen också har en. Behandla variabler som vanliga tal. Till exempel:
. Det betyder att du kan placera valfritt x utanför parentes om den andra termen också har en. Behandla variabler som vanliga tal. Till exempel:
 är ett annat sätt att säga
är ett annat sätt att säga  . Det betyder att du kan placera valfritt x utanför parentes om den andra termen också har en. Behandla variabler som vanliga tal. Till exempel:
. Det betyder att du kan placera valfritt x utanför parentes om den andra termen också har en. Behandla variabler som vanliga tal. Till exempel: kan faktoriseras, eftersom båda termerna innehåller ett t. Det slutliga svaret blir
- Du kan till och med placera flera variabler utanför parenteser samtidigt. Till exempel i
båda termerna innehåller samma
. Du kan lösa upp detta

2. Erkänn ännu inte förenklade binomialer genom att kombinera liknande termer. Ta till exempel uttrycket  . Här verkar det som om du har att göra med fyra termer, men om du tittar närmare kommer du att inse att det bara finns två. Du kan lägga till liknande termer och eftersom både 6 och 14 inte har någon variabel och 2x och 3x delar samma variabel, kan de slås samman. Upplösning är då lätt:
. Här verkar det som om du har att göra med fyra termer, men om du tittar närmare kommer du att inse att det bara finns två. Du kan lägga till liknande termer och eftersom både 6 och 14 inte har någon variabel och 2x och 3x delar samma variabel, kan de slås samman. Upplösning är då lätt:
 . Här verkar det som om du har att göra med fyra termer, men om du tittar närmare kommer du att inse att det bara finns två. Du kan lägga till liknande termer och eftersom både 6 och 14 inte har någon variabel och 2x och 3x delar samma variabel, kan de slås samman. Upplösning är då lätt:
. Här verkar det som om du har att göra med fyra termer, men om du tittar närmare kommer du att inse att det bara finns två. Du kan lägga till liknande termer och eftersom både 6 och 14 inte har någon variabel och 2x och 3x delar samma variabel, kan de slås samman. Upplösning är då lätt:





3. Erkänn den speciella "skillnaden mellan perfekta rutor". En perfekt kvadrat är ett tal vars rot är ett heltal, som t.ex 
 ,
, 
 , eller ens
, eller ens 
 Om ditt binomial är en minussumma med två perfekta kvadrater, som t.ex
Om ditt binomial är en minussumma med två perfekta kvadrater, som t.ex  , då kan du bara använda dem i den här formeln:
, då kan du bara använda dem i den här formeln:

 ,
, 
 , eller ens
, eller ens 
 Om ditt binomial är en minussumma med två perfekta kvadrater, som t.ex
Om ditt binomial är en minussumma med två perfekta kvadrater, som t.ex  , då kan du bara använda dem i den här formeln:
, då kan du bara använda dem i den här formeln:





4. Lär dig att förenkla "skillnaden mellan perfekta kuber". Precis som de perfekta kvadraterna är detta en enkel formel där två kuber subtraheras från varandra. Till exempel,  . Som tidigare, hitta kubroten för var och en och använd den i formeln:
. Som tidigare, hitta kubroten för var och en och använd den i formeln:
 . Som tidigare, hitta kubroten för var och en och använd den i formeln:
. Som tidigare, hitta kubroten för var och en och använd den i formeln:

![Factoring binomialer {sqrt[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Factoring binomialer {sqrt[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)


5. Vet att summan av perfekta kuber också passar in i en formel. Till skillnad från skillnaden mellan perfekta rutor kan du använda tillagda kuber, som t.ex  , också lätt att hitta med en enkel formel. Detta är nästan exakt samma som ovan, men med några plus och minus omvända. Formeln är lika enkel som de andra två, och allt du behöver göra är att känna igen de två kuberna i problemet:
, också lätt att hitta med en enkel formel. Detta är nästan exakt samma som ovan, men med några plus och minus omvända. Formeln är lika enkel som de andra två, och allt du behöver göra är att känna igen de två kuberna i problemet:
 , också lätt att hitta med en enkel formel. Detta är nästan exakt samma som ovan, men med några plus och minus omvända. Formeln är lika enkel som de andra två, och allt du behöver göra är att känna igen de två kuberna i problemet:
, också lätt att hitta med en enkel formel. Detta är nästan exakt samma som ovan, men med några plus och minus omvända. Formeln är lika enkel som de andra två, och allt du behöver göra är att känna igen de två kuberna i problemet:

![Factoring binomialer {sqrt[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Factoring binomialer {sqrt[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)

Tips
- Alla binomialer har inte gemensamma delare! Vissa har redan förenklats så mycket som möjligt.
- Om du inte är säker på om det finns en gemensam divisor, dividera med mindre tal först. Om du till exempel inte direkt ser att 16 är den gemensamma divisorn för 32 och 16, börja dividera båda talen med 2. Detta lämnar 16 och 8, som också kan delas med 8. Nu har du 2 och 1, de minsta faktorerna. Det finns helt klart en gemensam divisor större än 8 och 2.
- Observera att en sjätte potens (x) båda är en perfekt kvadrat och är en perfekt kub. Så du kan tillämpa vilken som helst specialformel ovan, i valfri ordning, på ett binomial som är skillnaden mellan perfekta sjättepotenser, som x - 64. Det kan dock vara lättare att tillämpa differensformeln för perfekta kvadrater först så att du kan faktorisera binomialet ytterligare.
Varningar
- Ett binomial som är summan av perfekta kvadrater kan inte faktoriseras.
Оцените, пожалуйста статью