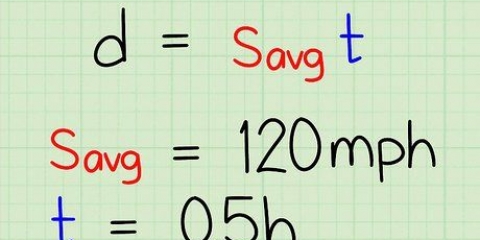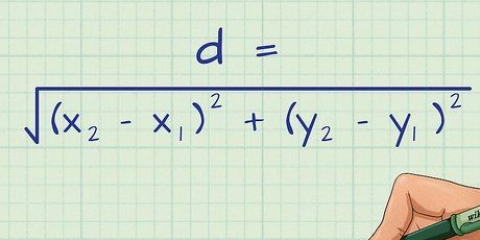Glöm inte heller att koppla ihop startpunkten med slutpunkten, med hjälp av en rak linje.Detta är förskjutningen vi ska beräkna. Till exempel, om ett föremål färdas först 300 meter i östlig riktning och sedan 400 meter i nordlig riktning, bildas en rätvinklig triangel. AB är den första sidan och BC är den andra sidan av triangeln.AC är triangelns hypotenusa och dess värde är objektets förskjutning. I det här exemplet är de två riktningarna "öster" och "norr." 
Till exempel, x = 300 och y = 400.Din ekvation ser nu ut så här: s = √300² + 400². 
Till exempel: s = √90000 + 160000.s = √250000.s = 500.Du vet nu att förskjutningen är lika med 500 meter. 

Ekvationen kommer att se ut så här: s = 1/2(20 + 23)45. 
För den här ekvationen spelar det ingen större roll om du av misstag byter ut den initiala och slutliga hastigheten. Eftersom du lägger ihop dessa värden först, spelar det ingen roll. Men i andra ekvationer kan byte av initiala och slutliga hastigheter påverka det slutliga svaret, eller värdet på förskjutningen. Din ekvation ser nu ut så här: s = 1/2(43)45.Dela först 43 med 2, vilket ger 21,5 som svar. Multiplicera 21,5 med 45, vilket ger 967,5 meter som svar.967,5 är bilens slagvolym, sett från startpunkten. 

Baserat på exemplet ovan bör din ekvation nu se ut så här: s = 25(4) + 1/2(3)4².Det kan säkert hjälpa om du sätter parenteser runt accelerations- och tidsvärdena för att hålla siffrorna åtskilda från varandra. 
Låt oss titta närmare på ekvationen: s = 25(4) + 1/2(3)4². Ordningen är: 4² = 16; sedan 16 x 3 = 48; sedan 25 x 4 = 100; och om senast 48/2 = 24. Ekvationen ser nu ut så här: s = 100 + 24.Efter addition ger detta s = 124, så förskjutningen är 124 meter. 

Ett exempel på en uppgift: En tjej sitter på en karusell. Hennes säte är på ett avstånd av 1 meter från mitten av cirkeln (radien). Om flickan rör sig längs en 1,5 meter lång cirkelbåge (linjär förskjutning), vad är hennes vinkelförskjutning? Ekvationen ser ut så här: θ = 1,5/1. 
Efter division 1,5/1 står du kvar med 1,5.Flickans vinkelförskjutning är 1,5 radianer. Eftersom vinkelförskjutning indikerar hur mycket ett föremål har roterats från sin hemposition, är det nödvändigt att representera detta i radianer, inte som ett avstånd. Radianer är enheter som används för att mäta vinklar. 

Förskjutning kallas också a "vektorkvantitet" hänvisas till som förändringen av ett objekts position jämfört med riktningen i vilken objektet rör sig. Anta att du går 5 meter österut. Går du 5 meter västerut igen så rör du dig i motsatt riktning, tillbaka till din startpunkt. Även om du har gått totalt 10 meter har din position inte ändrats och din förskjutning är därför 0 meter. 
Tänk dig en fotbollstränare som studsar fram och tillbaka längs sidlinjen.Medan han gett instruktioner till spelarna har han gått längs linjen flera gånger, fram och tillbaka. Om du hela tiden skulle hålla ett öga på tränaren skulle du se hur långt han åker. Men anta att tränaren stannar för att säga något till en försvarare? Om han är på en plats som skiljer sig från hans utgångspunkt, så tittar du på tränarens rörelse (vid ett visst ögonblick). 
En krökt stig kommer så småningom att leda dig från startpunkt till slutpunkt, men detta är inte den kortaste vägen. För att hjälpa dig att visualisera detta, föreställ dig att gå i en rak linje och bli stoppad av en pelare eller annat hinder. Du kan inte gå igenom pelaren, så du går runt den. Även om du hamnar på samma ställe som om du hade gått rakt igenom pelaren så fick du ändå resa en längre väg för att komma dit. Även om förskjutningen helst är i en rak linje, är det möjligt att mäta förskjutningen av ett föremål som "väl" rör sig längs en krokig stig. Detta kallas för "vinkelförskjutning" och det kan beräknas genom att hitta det kortaste avståndet som finns mellan startpunkt och slutpunkt. 
Anta till exempel att du går 5 meter österut och sedan 3 meter västerut. Även om du tekniskt sett är 2 meter från din startpunkt är förskjutningen -2 eftersom du rör dig i motsatt riktning vid den punkten.Avståndet kommer alltid att vara positivt, eftersom du inte vet en sträcka du har rest "uppknäppt" kan göra. Negativ förskjutning betyder inte att förskjutningen minskar. Det är helt enkelt ett sätt att indikera att rörelsen är i motsatt riktning. 
Så detta är bara möjligt om du rör dig i en rak linje från startpunkten, och utan att ändra riktning efteråt.Anta till exempel att du bor i San Francisco, Kalifornien och får ett jobb i Las Vegas, Nevada. Du måste då flytta till Las Vegas för att bo närmare jobbet. Om du tar flyget, ett direktflyg från San Francisco till Las Vegas, har du rest 670 km och ditt deplacement är därför 670 km. Men om du reser med bil från San Francisco till Las Vegas kan ditt avstånd fortfarande vara 670 km men du har rest 906 km under tiden.Eftersom körning vanligtvis innebär en riktningsändring (avstängning, ta en annan rutt), har du färdats mycket längre än det kortaste avståndet mellan de två städerna.
Beräkna förskjutning
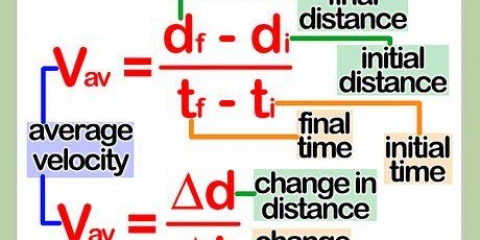
Termen förskjutning i fysiken syftar på förändringen snarare än ett objekt. Vid beräkning av förskjutning mäter du hur mycket ett objekt har rört sig, baserat på data från startposition och slutposition. Formeln du använder för att bestämma förskjutningen beror på de variabler som anges för ett problem. Ta följande steg för att lära dig hur man beräknar förskjutningen av ett föremål.
Steg
Del 1 av 5: Beräkna den resulterande förskjutningen

1. Använd formeln för den resulterande förskjutningen med den längdenhet som används för att ange start- och slutposition. Även om avstånd skiljer sig från förskjutning, kommer ett uttalande om resulterande förskjutning att indikera hur mycket "meter" har kasserat ett föremål. Använd dessa måttenheter för att beräkna förskjutningen, hur långt ett föremål är från sin ursprungliga plats.
- Ekvationen för den resulterande förskjutningen är: s = √x²+y²."s" står för förskjutning.X är den första riktningen objektet rör sig och y är den andra riktningen objektet rör sig. Om ditt objekt bara rör sig i en riktning, då är y = 0.
- Ett objekt kan bara röra sig i maximalt 2 riktningar, eftersom att flytta längs linjen nord-sydlig eller öst-västlig linje anses vara neutral.

2. Anslut prickarna enligt rörelseordningen och märk dessa prickar från A-Z.Använd en linjal för att rita raka linjer från punkt till punkt.

3. Ange värdena för x² och y².Nu när du vet i vilken riktning ditt objekt rör sig kan du börja fylla i värdena för de relevanta variablerna.

4. Träna ut ekvationen. Beräkna först 300² och sedan 400², addera dem och subtrahera kvadratroten ur summan.
Del 2 av 5: Att känna till hastighetsvektorn och tidslängden

1. Använd denna formel om problemet ger hastighetsvektorn och tidslängden. Det kan hända att ett fysikproblem inte säger ett ord om tillryggalagd sträcka, utan anger hur länge ett föremål har färdats och med vilken hastighet. Du kan sedan beräkna förskjutningen med hjälp av tidslängden och hastigheten.
- I det här fallet kommer ekvationen att se ut så här: s = 1/2(u + v)t.u = objektets initiala hastighet, den hastighet med vilken objektet började röra sig i en viss riktning.v = objektets sluthastighet, eller hur snabbt det gick i slutet. t = den tid det tog objektet att nå sin destination.
- Till exempel: En bil kör i 45 sekunder.Bilen svängde åt väster med en hastighet på 20 m/s (starthastighet) och i slutet av gatan är hastigheten 23 m/s (sluthastighet). Beräknade förskjutningen baserat på dessa data.

2. Ange värden för hastighet och tid. Nu när du vet hur länge bilen har kört, och vad start- och sluthastigheten var, kan du hitta avståndet från startpunkten till slutpunkten.

3. Träna ut ekvationen när du har skrivit in värdena. Kom ihåg att beräkna termerna i rätt ordning annars blir förskjutningen fel.
Del 3 av 5: När hastighet, acceleration och tid anges

1. En annan ekvation är nödvändig om accelerationen anges för ett problem, tillsammans med hastigheten och tiden. Med en sådan uppgift vet du vad objektets initiala hastighet har varit, vilken acceleration och hur länge objektet har varit på vägen. Du behöver följande ekvation.
- Ekvationen för denna typ av problem ser ut så här: s = ut + 1/2at².De "du" representerar fortfarande den initiala hastigheten; De "a" är objektets acceleration, eller också hur snabbt objektets hastighet ändras. Variabeln"t" kan antingen betyda den totala tiden, eller så kan det indikera en specifik period under vilken objektet har accelererat. Hur som helst, detta indikeras i tidsenheter som sekunder, timmar osv.
- Antag att en bil med en starthastighet på 25 m/s får en acceleration på 3 m/s2 under en period av 4 sekunder.Vad är bilens förskjutning efter 4 sekunder?

2. Fyll i värdena på rätt plats i ekvationen. Till skillnad från föregående ekvation visas bara den initiala hastigheten här, så se till att du anger rätt värden.

3. Beräkna förskjutningen genom att lösa ekvationen. Ett snabbt sätt att hjälpa dig komma ihåg operationsordningen i en ekvation är mnemoniken "Mr. Dale som väntar på svar".Indikerar alla aritmetiska operationer i rätt ordning (överdrift, multiplikation, division, kvadratur, addition och subtraktion).
Del 4 av 5: Beräkna vinkelförskjutningen

1. Bestämma vinkelförskjutningen när ett föremål rör sig längs en kurva. Även om detta fortfarande innebär att beräkna förskjutningen med en rak linje, behöver du skillnaden mellan start- och slutpositionen längs en krökt bana.
- Ta som exempel en tjej som är på karusell. När hon snurrar runt utsidan av hjulet rör sig hon i en cirkel. Vinkelförskjutning försöker hitta det kortaste avståndet mellan start- och slutposition om ett föremål inte rör sig i en rät linje.
- Formeln för vinkelförskjutningen är: 6 = S/r, varigenom "s" står för den linjära förskjutningen, "r" för radien, och "θ" vinkelförskjutningen är.Linjär förskjutning är avståndet ett föremål färdas längs en cirkel.Radien är avståndet för ett föremål från cirkelns mitt.Vinkelförskjutning är ett värde vi vill veta.

2. Anslut värdena för den linjära förskjutningen och radien i ekvationen. Kom ihåg att radien är avståndet från mitten av en cirkel till kanten; det kan vara så att diametern är angiven för ett problem, i så fall måste du dividera det med 2 för att hitta radien (radien) för cirkeln.

3. Dividera den linjära förskjutningen med radien.Detta kommer att ge dig objektets vinkelförskjutning.
Del 5 av 5: Förstå förskjutning

1. Det är viktigt att förstå det "distans" ibland betyder något annat än "förflyttning."Avstånd säger något om hur långt ett föremål totalt har rört sig.
- Avstånd är något vi också kallar a "skalär" att nämna. Det är ett sätt att indikera hur lång sträcka du har rest, men säger ingenting om riktningen du har rört dig.
- Om du till exempel går 2 meter österut, 2 meter söderut, 2 meter västerut och igen 2 meter norrut är du tillbaka vid din startpunkt. Även om du har rest en total sträcka på 10 meter, är din förskjutning lika med 0 meter, eftersom din slutpunkt är lika med din startpunkt.

2. Förskjutning är skillnaden mellan två punkter. Förskjutning är inte en summa av rörelser som är fallet med avstånd; det handlar bara om delen mellan din start och din slutpunkt.

3. Kom ihåg orden väl "fram och tillbaka" när man försöker föreställa sig en förskjutning. Den motsatta riktningen ångrar rörelsen i den ursprungliga riktningen.

4. Förskjutningen mäts längs en rät linje, inte längs en cirkulär bana. För att ta reda på rörelsen letar du efter den kortaste vägen mellan två olika punkter.

5. Förstå att förskjutning också kan ha ett negativt värde, till skillnad från avstånd. Om slutpunkten nås genom att röra sig i en riktning motsatt den riktning du startade (relativt startpunkten), då är din förskjutning negativ.

6. Inse att avstånds- och förskjutningsvärdena ibland kan vara desamma. Om du går rakt 25 meter och sedan stannar är sträckan du har färdats lika med förskjutningen, helt enkelt för att du inte har ändrat riktning.
Tips
- Arbeta exakt
- Lär dig inte formlerna utantill, utan försök förstå hur de fungerar
Förnödenheter
- Kalkylator
- Avståndsmätare
"Beräkna förskjutning"
Оцените, пожалуйста статью