Observera dock att om tidsenheterna som används i ditt medelhastighetsvärde skiljer sig från dem i ditt tidsvärde, måste du konvertera den ena eller den andra för att matcha. Till exempel, om en medelhastighet mäts i km/h och tiden är i minuter, måste du dividera tiden med 60 för att omvandla den till timmar. Låt oss lösa vårt exempelproblem. 120 km/h × 0,5 h = 60 km. Observera att tidsenheterna (timmar) falla bort mot enheterna i nämnaren av medelhastigheten (timmar), vilket bara lämnar enheterna för avstånd (km). 
Anta att vi vet att en bil har gått 60 km på 50 minuter, men vi har inget värde för medelhastigheten under körning. I det här fallet kan vi använda variabeln spärla isolera i basekvationen för avståndet, och vi får spärla = d/t att få. Då beräknar vi 60 km/50 minuter = 1,2 km/min. Observera att i vårt exempel har vårt svar för hastighet en ovanlig enhet (km/minut). För att få ditt svar i den vanligaste formen av km/h, multiplicera det med 60 minuter/h och få `72 km/h att få. 
Exempel: I exemplet ovan drog vi slutsatsen att för att färdas 60 km på 50 minuter måste vi färdas i 72 km/h. Detta är dock bara sant om vi färdas med en hastighet under hela resan. Till exempel, genom att köra hälften av resan i 80 km/h och den andra hälften i 64 km/h, kör vi fortfarande 60 km på 50 minuter — 72 km/h = 60 km/50 min = ????? Matematiska lösningar att använda derivator är ofta ett bättre val än avståndsformeln för att definiera ett objekts hastighet i verkliga situationer, eftersom förändringar i hastighet är troliga. 

Observera att denna formel använder absoluta värden (symbolen |). Absoluta värden betyder helt enkelt att termerna i symbolerna blir positiva när de är negativa. Låt oss till exempel säga att vi stannar på en helt rak vägsträcka längs vägen. Om det finns en liten stad 5 km framför oss och en stad 1 km bakom oss, hur långt ifrån varandra är de två städerna?? Om vi tar stad 1 som x1 = betrakta 5 och stad 2 som x2 = -1, då kan vi hitta d, avståndet mellan de två städerna, enligt följande: d = |x2 - X1| = |-1 - 5| = |-6| = 6 km. 
Avståndsformeln i tvådimensionellt utrymme använder Pythagoras sats, som säger att hypotenusan i en rätvinklig triangel är lika med kvadratroten av de två andra sidorna. Låt oss till exempel säga att vi har två punkter i x-y-planet: (3, -10) och (11, 7) som representerar mitten av en cirkel respektive en punkt på cirkeln. För att hitta det raka avståndet mellan dessa två punkter kan vi lösa följande: d = √((x2 - X1) + (y2 - y1)) d = √((11 - 3) + (7 - -10)) d = √(64 + 289) d = √(353) = 18,79 
Exempel: Låt oss säga att som en astronaut som svävar i rymden nära två asteroider. Den ena är cirka 8 km framför oss, 2 km till höger om oss och 5 km under oss, medan den andra är 3 km bakom oss, 3 km till vänster om oss och 4 km ovanför oss. Om vi representerar positionerna för dessa asteroider med koordinaterna (8.2,-5) och (-3,-3.4), kan vi hitta avståndet mellan de två enligt följande: d = √((-3 - 8) + (-3 - 2) + (4 - -5)) d = √((-11) + (-5) + (9)) d = √(121 + 25 + 81) d = √(227) =15,07 km
Beräkna avstånd
Avstånd, ofta kallad variabeln d, är ett mått på det utrymme som upptas av en rät linje mellan två punkter. Avstånd kan hänvisa till utrymmet mellan två stationära punkter (till exempel är en persons höjd avståndet från botten av hans eller hennes fötter till toppen av hans eller hennes huvud) eller kan hänvisa till utrymmet mellan den aktuella positionen för en rörlig objekt och dess startplats. De flesta avståndsproblem kan lösas med ekvationerna d = spärla × t där d är avståndet, spärla medelhastigheten och t tiden, eller ekvationen d = √((x2 - X1) + (y2 - y1)), där (x1, y1) och (x2, y2) är x- och y-koordinaterna för två punkter.
Steg
Metod 1 av 2: Bestäm avstånd med medelhastighet och tid

1. Bestäm värdena för medelhastighet och tid. När man försöker hitta avståndet ett rörligt föremål har färdats, är två delar av information avgörande för att göra denna beräkning: fart` (eller hastighetsstorlek) ochtid vart föremålet flyttades. Med dessa data är det möjligt att hitta den sträcka som objektet tillryggalagt, med hjälp av formeln d = spärla × t.
- För att bättre förstå tillämpningen av avståndsformeln ska vi i det här avsnittet lösa ett exempelproblem. Låt oss säga att vi kör i cirka 120 km/h och vill veta hur långt vi kommer att åka på en halvtimme. Av 120 km/h som vårt värde för medelhastigheten och 0,5 timmar som vårt värde för tid kommer vi att lösa detta problem i nästa steg.

2. Multiplicera medelhastigheten med tiden. När du väl vet medelhastigheten för ett rörligt föremål och den tid det tog att röra sig, är det relativt enkelt att hitta avståndet det har färdats. Multiplicera bara dessa två värden tillsammans för att få ditt svar.

3. Redigera ekvationen för att lösa de andra variablerna. Enkelheten för den grundläggande avståndsekvationen (d = spärla × t) gör det ganska enkelt att använda ekvationen för att hitta värden för variabler utöver avstånd. Isolera variabeln du vill lösa enligt grundreglerna för matematik, och skriv sedan in värdena för de andra två variablerna för att hitta värdet på den tredje. Med andra ord, för att hitta medelhastigheten för ditt objekt, använd ekvationen spärla = d/t och för att ta reda på tiden som ett föremål har färdats, använd ekvationen t = d/spärla.

4. Observera att variabeln `spärla` i avståndsformeln hänvisar till genomsnitt fart. Det är viktigt att förstå att standardavståndsformeln ger en förenklad bild av ett objekts rörelse. Avståndsformeln antar att det rörliga föremålet har en konstant hastighet har — med andra ord, det antar att det rörliga föremålet rör sig med en `likformig`, oföränderlig hastighet. För abstrakta matematiska problem, som de som uppstår i en akademisk miljö, är det ibland fortfarande möjligt att modellera ett objekts rörelse med detta antagande. I verkligheten representerar dock denna modell ofta inte rörelsen hos rörliga föremål, som i verkligheten kan accelerera, bromsa, stanna och vända över tiden.
Metod 2 av 2: Bestämma avståndet mellan två punkter

1. Bestämma två punkter i ett plant utrymme. Tänk om du istället för att bestämma avståndet ett rörligt föremål har färdats, måste bestämma avståndet mellan två stationära föremål? I fall som detta kommer den hastighetsbaserade distansformeln som beskrivs ovan inte att vara till någon nytta. Lyckligtvis finns det en annan avståndsformel för att snabbt hitta det kortaste avståndet mellan två punkter. Men för denna formel behöver du känna till koordinaterna för de två punkterna. Om du har att göra med ett endimensionellt avstånd (som på en tallinje), är dina koordinater två tal, x1 och x2. Om du har att göra med avstånd i två dimensioner behöver du värden för två punkter (x,y), (x)1,y1) och (x2,y2). Slutligen, för tre dimensioner behöver du värden för (x1,y1,z1) och (x2,y2,z2).

2. Bestäm avståndet på en linje genom att subtrahera värdet på koordinaterna för de två punkterna. Det är enkelt att beräkna det endimensionella avståndet mellan två punkter om du vet värdet för varje punkt. Använd bara formeln d = |x2 - X1|. I den här formeln subtraherar du x1 av x2 och ta det absoluta värdet av ditt svar för att hitta avståndet mellan x1 och x2 att hitta. Normalt använder man den endimensionella avståndsformeln när de två punkterna ligger på en tallinje eller axel.

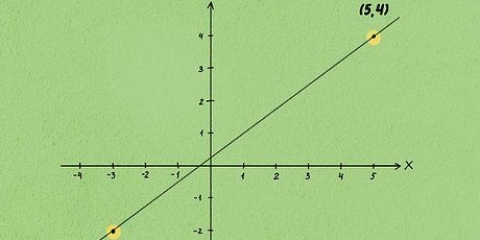
3. Hitta avståndet i planet med hjälp av Pythagoras sats. Att hitta avstånd mellan två punkter i tvådimensionellt utrymme är mer komplicerat än i en dimension, men inte svårt. Använd bara formeln d = √((x2 - X1) + (y2 - y1)). I den här formeln subtraherar du de två x-koordinaterna, kvadrerar resultatet, subtraherar y-koordinaterna, kvadrerar resultatet, adderar de två mellanresultaten och beräknar kvadratroten för att hitta avståndet mellan de två punkterna för att hitta. Den här formeln fungerar i det tvådimensionella planet - till exempel på standard x/y-diagram.

4. Bestäm det tredimensionella avståndet genom att ändra areaformeln. I tre dimensioner har punkter även en z-koordinat utöver x- och y-koordinaten. För att hitta avståndet mellan två punkter i tredimensionellt utrymme, använd d = √((x2 - X1) + (y2 - y1) + (z2 - z1)). Detta är en modifierad form av den tvådimensionella avståndsformeln som beskrivs ovan som också tar hänsyn till z-koordinaterna. Genom att subtrahera de två z-koordinaterna från varandra, kvadrera dem och köra igenom resten av formeln enligt beskrivningen ovan, är du säker på att ditt slutliga svar återspeglar det tredimensionella avståndet mellan de två punkterna.
"Beräkna avstånd"
Оцените, пожалуйста статью