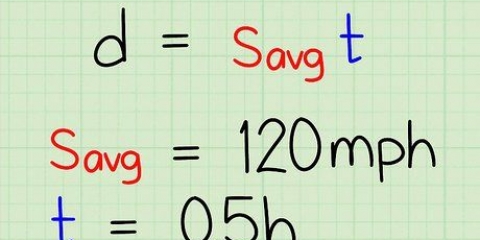I vårt exempel, låt oss säga att det är exakt klockan två kostnad för att göra denna resa. 
I vårt exempel är denna ekvation 100 miles/2 timmar = 50 miles/timme(ca 80 km/h). 
Enheterna för hastighet är enheterna för avstånd över tidsenheterna. I vårt exempel är våra enheter miles/timme (eller miles per timme) eftersom vi mätte avstånd i miles och tid i timmar. 

Låt oss till exempel säga att vi i exemplet ovan behöver vårt svar in mil istället för kilometer. Det är cirka 1,6 kilometer i en mil, så vi kan konvertera det så här: Observera att eftersom kilometer är längst ner i bråkdelen, kan den strykas över med kilometerna i det ursprungliga svaret och lämna svaret i miles. Den här webbplatsen innehåller omvandlingar för de vanligaste enheterna. 
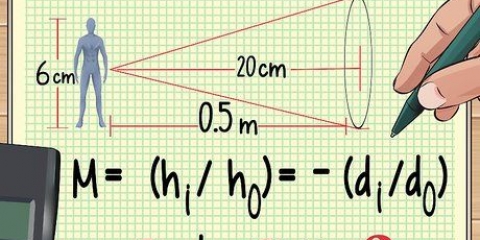
Låt oss till exempel säga att ett plan flyger fem gånger i en cirkel som är 20 miles bred. Planet genomför denna resa på en halvtimme. I det här exemplet måste vi fortfarande bestämma exakt hur långt planet har färdats innan vi kan hitta hastigheten. Vi kan använda ekvationen för avståndet runt en cirkel (dess omkrets) istället för "a" i vår jämförelse. Denna ekvation är omkrets = 2πr där r = cirkelns radie. Vi kan lösa detta på följande sätt: 
För att illustrera denna skillnad, föreställ dig den senaste resan du gjorde i en bil. Det är högst osannolikt att du har färdats i samma hastighet hela resan. Istället började du långsamt och nådde gradvis din topphastighet och saktade ner vid trafikljus, bilköer och så vidare. Om du använder standardhastighetsekvationen för att beräkna din hastighet för resan, återspeglas inte dessa hastighetsändringar. Istället får du ett svar någonstans mellan de olika hastigheterna du har färdats med. 

Av denna anledning har båda bilarna i exemplet ovan en hastighet (hastighet) förbi 50 km/h. 
Antag att ett objekts position i meter ges av ekvationen 3t + t - 4 där t = tiden i sekunder. Vi vill veta vad objektets hastighet är vid t = 4 sekunder. I det här fallet kan vi lösa detta på följande sätt: Nu fyller vi i t = 4: 
Antag att ett objekt har en konstant acceleration (i m/s givet av a (t) = -30. Låt oss också säga att föremålet har en initialhastighet på 10 m/s. Vi måste hitta hastigheten vid t = 12s. I det här fallet kan vi lösa detta på följande sätt: För att hitta C löser vi v(t) för t = 0. Kom ihåg att objektets initiala hastighet är 10 m/s. Nu kan vi ange t = 12 sekunder.
Beräkna hastighet
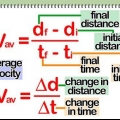
Hastighet är måttet på "hur snabbt" något går vid ett givet ögonblick. Om du någon gång har tittat på en bils hastighetsmätare medan du kör, har du sett hur hastigheten mäts - ju längre nålen går, desto snabbare blir bilens hastighet. Det finns några olika sätt att beräkna hastighet, beroende på vilken information du har. För allmänna ändamål är ekvationen hastighet = avstånd/tid (eller s = a/t) vanligtvis det enklaste sättet att beräkna hastighet.
Steg
Metod 1 av 3: Användning av standardhastighetsekvationen

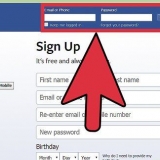
1. Hitta avståndet ett objekt har färdats. Den grundläggande ekvationen de flesta använder för att ta reda på hur snabbt något går är väldigt lätt att använda. Det första du behöver veta är hur lång sträcka objektet har tillryggalagt. Med andra ord, hur långt är startpunkten från slutpunkten?
- Denna ekvation blir lättare att förstå med ett exempel. Låt oss säga att vi tar en biltur till en nöjespark 100 mil (cirka 161 kilometer). I de kommande stegen kommer vi att använda denna information för att lösa denna ekvation.

2. Hitta den tid det tog objektet att färdas den sträckan. Nästa information du behöver är hur lång tid det tog objektet att resa. Med andra ord, hur lång tid tog det att komma från startpunkten till slutpunkten?

3. Dela avståndet med tiden för att hitta hastigheten. Allt du behöver är dessa två delar av information för att bestämma din hastighet för resan. Avståndet handla om tiden ger dig objektets hastighet.

4. Glöm inte enheterna. Märk ditt svar med lämpliga enheter (som miles per timme, etc.) är kritisk. Utan enheter kan det vara svårt för andra att förstå vad ditt svar betyder. Du kan också förlora poäng om du glömmer att skriva ned enheten på en skoluppgift.
Metod 2 av 3: Lösning av andra problem

1. Isolera de olika variablerna för att beräkna avstånd och tid. När du väl känner till grunderna i hastighetsekvationen kan du använda den för att hitta mer än bara hastighet. Om du till exempel känner till hastigheten och en av de andra variablerna kan du ordna om ekvationen för att hitta den information som saknas.
- Anta att vi vet att ett tåg har färdats med en hastighet av 20 kilometer i timmen i fyra timmar, men vi behöver veta avståndet det färdats. I det här fallet kan vi ordna om ekvationen och lösa den så här:
- hastighet = avstånd/tid
- hastighet × tid = (avstånd/tid) × tid
- hastighet × tid= avstånd
- 20 km/h × 4 h = avstånd = 80 kilometer

2. Konvertera dina enheter om det behövs. Ibland kan man räkna ut hastigheten i en annan enhet än man behöver. I det här fallet bör du omvandlingsfaktorer använd för att lägga ditt svar i rätt enhet. För att göra detta, skriv sambanden mellan dina enheter som bråk och multiplicera. När du multiplicerar roterar du din bråkdel efter behov för att bli av med de enheter du inte vill ha. Det här är mycket lättare än det låter!
- 80 kilometer × 1 mil/1.6 kilometer = 50 mil

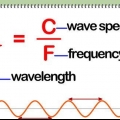
3. Byt ut variabeln "avstånd" med avståndsformler om det behövs. Objekt färdas inte alltid i snygga, bekväma raka linjer. Om inte, kanske du inte helt enkelt kan infoga ett numeriskt värde för avstånd i standardhastighetsekvationen. Istället kan du behöva ersätta a i s = a/t med en formel som modellerar avståndet objektet har tillryggalagt.
- s = (2 × π × r)/t
- s = (2 × π × 10)/0.5
- s = 62.83/0.5 = 125.66 miles/timme

4. Se att s = a/t a genomsnitt hastighet ger. Den enkla, bekväma ekvationen vi använde för att hitta hastigheten har en stor brist. Värdet den ger är tekniskt sett en medelhastighet. Det betyder att det förutsätter att objektet du mäter har samma hastighet under hela resan. Som vi kommer att se nedan kan det vara svårare att hitta hastigheten på ett objekt vid varje given tidpunkt.
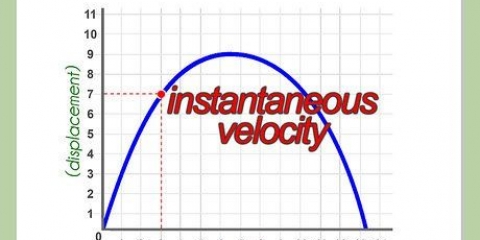
Metod 3 av 3: Beräkna momentan hastighet
Anmärkning: Det här avsnittet använder tekniker som är okända för dem som inte har studerat kalkyl. Se våra kalkylartiklar för hjälp.

1. Observera att hastighet definieras som hastighetens storlek. Hastighetsberäkningar på högre nivå kan vara förvirrande eftersom matematiker och vetenskapsmän använder olika definitioner för "hastighet". En hastighet (hastighet) har två komponenter: a magnitud och a riktning. Storleken är lika med objektets hastighet. En riktningsändring kommer att orsaka en förändring i hastighet (hastighet), men inte i hastighet.
- Låt oss till exempel säga att två bilar kör i motsatta riktningar. Hastighetsmätarna på båda bilarna visar 50 km/h så båda har samma hastighet. Men eftersom de flyttar isär kan vi säga att en bil är en hastighet (hastighet) på -50 km/h och en har en hastighet (hastighet) från 50 km/h.
- Precis som du kan beräkna den momentana hastigheten (hastighet), kan du också beräkna beräkna momentan hastighet (hastighet).

2. Använd absoluta värden för negativa hastigheter. Objekt kan ha hastigheter av negativ storlek (om de rör sig i negativ riktning i förhållande till något annat). Det finns dock inget sådant som en negativ hastighet (hastighet) så i dessa fall absolutvärde storleken ändrar objektets hastighet.

3. Ta derivatan av en positionsfunktion. Om du har en funktion s(t) som ger dig positionen för ett objekt i förhållande till tiden, så kommer derivatan av s(t) att ge dig hastighet (hastighet) ge med hänsyn till tid. Anslut bara ett tidsvärde till denna ekvation för variabeln t (eller vad tidsvärdet nu är) för att få hastigheten vid denna punkt. Härifrån är det enkelt att hitta hastigheten.
- 3t + t - 4
- s`(t) = 2 × 3t + 1
- s`(t) = 6t + 1
- s`(t) = 6(4) + 1 = 24 + 1 = 25 meter/sekund. Detta är tekniskt sett en hastighetsmätning (hastighet) men eftersom den är positiv och riktning inte nämns i problemet kan vi i huvudsak använda den för hastighet.

4. Ta integralen av en accelerationsfunktion. Acceleration är ett sätt att förändring i ett objekts hastighet över tiden att mäta. Det här ämnet är lite för komplicerat för att fullständigt förklara i den här artikeln. Det är dock användbart att notera att när du har en funktion a(t) som ger acceleration i förhållande till tid, ger integralen av a(t) dig hastighet (hastighet) i förhållande till tid. Observera att det är användbart att känna till objektets initialhastighet så att du kan definiera konstanten som är resultatet av en obestämd integral.
- a(t) = -30
- v(t)= ∫ a(t)dt =∫ -30dt = -30t + C
- v(0) = 10 = -30(0) + C
- 10 = C, så v(t) = -30t + 10
- v(12) = -30(12) + 10 = -360 + 10 = -350. Eftersom hastighet är det absoluta värdet av hastighet, är objektets hastighet 350 meter/sekund.
Tips
- Övning ger färdighet! Försök att göra dina egna summor genom att ersätta olika tal i exemplen ovan.
- Om du letar efter ett snabbt sätt att beräkna för avancerade hastighetsberäkningar, använd här än online-derivatkalkylatorn och online-integralkalkylatorn här.
Оцените, пожалуйста статью