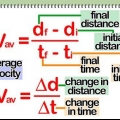
aav = /t (Tecknet Δ eller "delta" betyder bara "förändra.") aav = /(tf - ti) I denna ekvation är vf sluthastigheten och vi är starthastigheten. 
Från och med nu kommer vi att använda positiva siffror för att beskriva rörelsen till höger så att vi inte behöver ange riktningen varje gång. Om bilen startar framåt och slutar bakåt, se till att skriva den senaste hastigheten som ett negativt tal. 
Se till att hastigheten och tiden alltid skrivs i samma enheter. Till exempel, om din hastighet registreras i km/h, ska tiden också registreras i timmar. 
aav = /(10s - 0s) aav = /(10s) aav = 50 m/s/s Detta kan också noteras som 50 m/s. 
Bilen kunde starta i 0 m/s och accelerera kontinuerligt i 10 sekunder, tills den når 500 m/s. Bilen kunde starta i 0 m/s, accelerera snabbt till 900 m/s och sedan bromsa till 500 m/s från tionde sekunden. Bilen kunde starta i 0 m/s, stå stilla i 9 sekunder och accelerera mycket snabbt till 500 m/s från tionde sekunden. 

vslutet - vkomma igång = + eller - ? 
Det blå tåget rör sig snabbare längs den positiva sidan av linjen och accelererar därmed från +5 m/s till +7 m/s. Sluthastigheten minus initialhastigheten är 7 - 5 = +2. Eftersom förändringen i hastighet är positiv, så är accelerationen det också. Det röda tåget rör sig snabbare längs minussidan och börjar alltså med -5 m/s men slutar med -7 m/s. Sluthastigheten minus initialhastigheten är -7 - (-5) = -7 + 5 = -2 m/s. Eftersom förändringen i hastighet är negativ, så är accelerationen det också. 
Men om en helikopter flyger med en hastighet av -100 km i timmen och accelererar med -50 km i timmen, så finns det en positiv acceleration. Detta beror på att hastighetsändringen var positiv: -50 - (-100) = +50, även om hastighetsändringen inte var tillräcklig för att vända helikopterns riktning.
Beräkna medelacceleration
Acceleration är en storhet som beskriver en hastighetsändring och inkluderar både en hastighetsändring och en riktningsändring. Du behöver medelaccelerationen för att bestämma objektets medelhastighet över en given tid. Eftersom det inte är något som de flesta räknar på i det dagliga livet kan accelerationsproblem kännas lite konstigt, men med rätt tillvägagångssätt kommer du att förstå dem helt på kort tid.
Steg
Del 1 av 2: Beräkna medelaccelerationen

1. Förstå vad acceleration är. Acceleration beskriver hur snabbt något går snabbare eller saktar ner. Konceptet är så enkelt som det låter, även om din lärobok kanske beskriver det som "hastighetsändringen per tidsenhet." Accelerationen kan också beskriva i vilken riktning ett objekt rör sig, vilket du kan inkludera som en beskrivning eller som en del av formeln:
- Vanligtvis, om ett objekt flyttas till höger,upp ellerfram- drag noteras dessa som ett positivt (+) tal.
- Om ett objekt till vänster, ner, eller bakåt rörelser, använd ett negativt (-) tal för accelerationen.

2. Definitionen som en formel. Som nämnts ovan är acceleration hastighetsändringen per tidsenhet. Det finns två sätt att skriva detta som en formel:

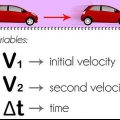
3. Bestäm objektets initiala och slutliga hastighet. Till exempel, om en bil accelererar från stillastående till 500 meter/sekund till höger, blir starthastigheten 0 m/s och sluthastigheten blir 500 m/s åt höger.

4. Lägg märke till förändringen över tid. Till exempel kan bilen behöva 10 sekunder för att nå sluthastighet. Om inte annat begärs i utlåtandet innebär detta vanligtvis tf = 10 sekunder och ti = 0 sekunder.

5. Använd dessa siffror för att beräkna medelaccelerationen. Lägg hastigheten och tiden i formeln för att hitta medelaccelerationen. I vårt exempel:

6. Förstår resultatet. Medelaccelerationen beskriver hur snabbt hastigheten ändras under den tid vi vill undersöka, i genomsnitt. Ovanstående exempel accelererade bilen till vänster och hastigheten ökade med 50 m/s varje sekund. Observera att exakta rörelsedata kan ändras så länge som bilen slutar med samma totala förändring i hastighet och tid:
Del 2 av 2: Förstå positiv och negativ acceleration

1. Vad den positiva och negativa hastigheten representerar.Även om vektorhastigheten alltid indikerar en viss riktning kan det bli irriterande att fortsätta upprepa "upp" eller "norr" eller "mot väggen" att behöva skriva. Istället antar de flesta problem att föremålet rör sig längs en rak linje. Vanligtvis indikeras en rörelse åt höger som positiv (+) och en rörelse åt vänster som negativ hastighet (-).
- Ett exempel: ett blått tåg färdas österut med en hastighet av 500 m/s. Ett rött tåg färdas västerut med samma hastighet, men eftersom det är i motsatt riktning skriver vi det som -500 m/s.

2. Använd definitionen av acceleration för att bestämma + eller – tecknen. Acceleration är förändringen i hastighet i förhållande till tiden. Om du inte är säker på om accelerationen är negativ eller positiv, se vad hastighetsförändringen är och vad du kan dra slutsatsen:

3. Acceleration förklarad i båda riktningarna. Antag att ett blått tåg och ett rött tåg kör ifrån varandra med en hastighet av 5 m/s. Vi kan föreställa oss detta på en tallinje, där det blå tåget rör sig med en hastighet av +5 m/s längs den positiva sidan av linjen, och det röda tåget rör sig längs den negativa sidan med en hastighet av -5 m/s. Om varje tåg börjar accelerera tills det når en hastighet 2 m/s snabbare i rörelseriktningen, har tåget en positiv eller negativ acceleration? Låt oss ta en titt:

4. Förstå fördröjning. Anta att ett flygplan har en starthastighet på 500 km i timmen och sedan saktar ner till 400 km i timmen. Även om det alltid rör sig i en positiv, framåtriktad riktning acceleration av flygplanet negativt, eftersom det "långsammare framåt" flytta sedan för det. Du kan kontrollera detta på samma sätt som i exemplen ovan: 400 - 500 = -100, så accelerationen är negativ.
Tips
- Acceleration och hastighet är båda vektorer, vilket betyder att de också indikerar rörelsens riktning. Kvantiteter som inte ger information om riktning kallas skalärer. Hastighet, längd och antalet äpplen i en korg är alla skalärer.
"Beräkna medelacceleration"
Оцените, пожалуйста статью