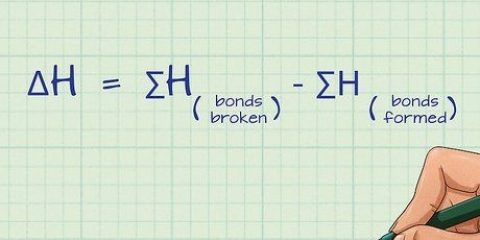
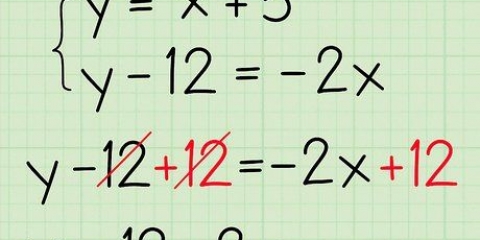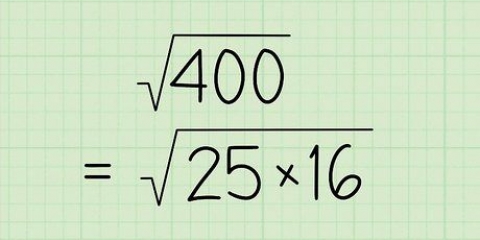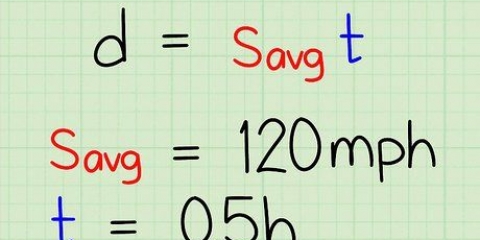Anta till exempel att uttalandet indikerar att det finns ett kärl fullt med vätska vid 295 K, vars ångtryck är lika med 1 atmosfär (atm). Frågan är: Vad är ångtrycket vid 393 K? Vi har två temperaturvärden och ett tryck, så vi kan hitta det andra tryckvärdet med Clausius-Clapeyrons ekvation. Ersätt värdena med variablerna och vi får ln(1/P2) = (ΔHvap/R)((1/393) - (1/295)). Observera att i Clausius-Clapeyrons ekvationer du alltid Kelvin används som temperatur. Du kan använda vilken enhet som helst för tryck, så länge de är lika för både P1 och P2. 
I vårt exempel, anta att vår vätska är rent vatten. Låt oss titta på en tabell med ΔHvap värden, då ser vi att ΔHvap ca 40,65 KJ/mol är. Eftersom vi använder joule för värdet av H (istället för kilojoule), kan vi konvertera detta till `40.650 J/mol.` Att skriva in konstanterna i vår ekvation ger ln(1/P2) = (40.650/8 314)((1/393) - (1/295)). 
Den enda knepiga punkten med att lösa vår ekvation (ln(1/P2) = (40.650/8,314)((1/393) - (1/295))) handlar om den naturliga logaritmen log(ln). Du kan eliminera detta genom att använda båda sidor av ekvationen som styrkan av den matematiska konstanten e. Således: `ln(x) = 2 → e = e → x = e.` Nu kan vi lösa vår ekvation: ln(1/P2) = (40.650/8.314)((1/393) - (1/295)) ln(1/P2) = (4.889,34)(-0,00084) (1/P2) = e 1/P2 = 0,0165 P2 = 0,0165 = `60,76 atm.Detta tycks stämma – i ett begränsat utrymme kommer en höjning av temperaturen med nästan 100 grader (till nästan 20 grader mer än vattnets kokpunkt) att skapa mycket vattenånga, vilket kraftigt ökar trycket. 

Låt oss i det här avsnittet illustrera begreppen vi diskuterar med ett enkelt exempel. Antag att vi vill bestämma ångtrycket för vanlig sirap. I allmänhet består vanlig sirap av en del socker löst i en del vatten, så det kan vi säga socker är det lösta ämnet och vatten är lösningsmedlet. Obs: Den kemiska formeln för sackaros (strösocker) är C12va22O11. Detta kommer snart att bli viktigt. 
Som ett exempel, låt oss säga att den nuvarande temperaturen på den vanliga sirapen 298 K (ca 25o C) är. 
Clausius-Clapeyron-ekvationen kan vara till hjälp här - använd referensvärdet för ångtryck och 298 K (25o C) för P1 respektive T1. I vårt exempel är blandningen 25o C, så vi kan använda de enkla referenstabellerna. Vi ser att vatten vid 25o C har ett ångtryck på 23,8 mm HG 
Antag att för vårt recept på sirap 1 liter (l) vatten och 1 liter sackaros (socker) behövs. I så fall måste vi hitta antalet mol av varje. För att göra detta bestämmer vi massan av var och en och omvandlar sedan ämnets molära massa till antalet Mol. Massa (1 l vatten): 1000 gram (g) Massa (1 l för råsocker): ca. 1.056,7 g Mol (vatten): 1000 gram × 1 mol / 18,015 g = 55,51 Mol Mullvad (sackaros): 1.056,7 gram × 1 Mol/342,2965 g = 3,08 mol (observera att du har molmassa av sackaros kan bestämma med den kemiska formeln, C12va22O11.) Totalt antal mol: 55,51 + 3,08 = 58,59 mol Molfraktion vatten: 55,51/58,59 = 0,947 
Efter att ha ersatt värdena får du: sidlösning = (23,8 mm Hg)(0,947) sidlösning = `22,54 mm Hg.` Detta verkar vara sant - när det gäller mol, bara lite socker löses i en stor mängd vatten (även om de faktiskt har samma volym), så ångtrycket kommer bara att minska något. 

Låt oss till exempel säga att det finns en okänd vätska med ett ångtryck på 25 torr vid 273 K och 150 torr vid 325 K, och vi vill bestämma förångningsentalpin för denna vätska (ΔHvap). Vi kan lösa detta om: ln(P1/P2) = (ΔHvap/R)((1/T2) - (1/T1)) (ln(P1/P2))/((1/T2) - (1/T1)) = (ΔHvap/R) R × (ln(P1/P2))/((1/T2) - (1/T1)) = ΔHvap Nu fyller vi i våra värderingar: 8,314 J/(K × Mol) × (-1,79)/(-0,00059) = ΔHvap 8,314 J/(K × Mol) × 3.033,90 = Hvap = 25.223,83 J/mol 
Anta till exempel att vi gjorde en lösning av två kemikalier: bensen och toluen. Den totala volymen av lösningen är 120 milliliter (ml); 60 ml bensen och 60 ml toluen. Lösningens temperatur är 25o C och ångtrycket för var och en av dessa kemikalier vid 25o C är 95,1 mm Hg för bensen och 28,4 mm Hg för toluen. Baserat på dessa värden måste du bestämma lösningens ångtryck. Vi kan göra detta enligt följande med standarddensiteten, molmassan och ångtrycket för våra två kemikalier: Massa (bensen): 60 ml = 0,060 1 &gånger 876,50 kg/1 000 l = 0,053 kg = 53 g Massa (toluen): 0,060 1 &gånger 866,90 kg/1.000 l = 0,052 kg = 52 g Mol (bensen): 53 g × 1 mol/78,11 g = 0,679 mol Mol (toluen): 52 g × 1 Mol/92,14 g = 0,564 Mol Totalt antal mol: 0,679 + 0,564 = 1,243 Molfraktion (bensen): 0,679/1,243 = 0,546 Molfraktion (toluen): 0,564/1,243 = 0,454 Lös: Plösning = PbensenXbensen + sidtoluenXtoluen sidlösning = (95,1 mmHg)(0,546) + (28,4 mmHg)(0,454) sidlösning = 51,92 mm Hg + 12,89 mm Hg = 64,81 mm Hg
Beräkna ångtrycket
Har du någonsin hört ett lätt väsande ljud när du öppnar en flaska vatten som du lämnat i den heta solen i några timmar? Detta orsakas av en princip som kallas ångtryck. Inom kemi är ångtryck det tryck som utövas på väggarna i ett slutet utrymme genom avdunstning (omvandlas till gas) av ett ämne. För att bestämma ångtrycket vid en given temperatur, använd Clausius-Clapeyrons ekvation: ln(P1/P2) = (ΔHvap/R)((1/T2) - (1/T1)).
Steg
Metod 1 av 3: Tillämpning av Clausius-Clapeyron-ekvationen

1. Skriv ner Clausius-Clapeyrons ekvation. Formeln för att beräkna ångtrycket som ger en förändring i ångtrycket över en tidsperiod kallas Clausius-Clapeyron-ekvationen (uppkallad efter fysikerna Rudolf Clausius och Benoît Paul Émile Clapeyron). Detta är formeln du vanligtvis behöver för att lösa vanliga ångtrycksproblem i fysik- och kemiklasser. Formeln ser ut så här: ln(P1/P2) = (ΔHvap/R)((1/T2) - (1/T1)). I denna formel hänvisar variablerna till:
- Hvap: Entalpin för avdunstning av en vätska. Du kan vanligtvis hitta dessa i en tabell längst bak i en lärobok i kemi.
- R: Den faktiska gaskonstanten, eller 8,314 J/(K × Mol).
- T1: Den temperatur för vilken ångtrycket är känt (d.v.s. den initiala temperaturen).
- T2: Den temperatur för vilken ångtrycket ska bestämmas (dvs sluttemperaturen).
- P1 och P2: Ångtrycket vid temperaturerna T1 respektive T2.

2. Byt ut de variabler du känner till. Clausius-Clapeyron-ekvationen ser knepig ut eftersom den innehåller så många olika variabler, men det är egentligen inte så svårt, så länge du har rätt information. De enklaste ångtrycksproblemen ger dig två temperaturvärden och värdet av ett tryck, eller två tryck och en temperatur - när du väl har dessa är det enkelt att lösa dem.

3. Ange konstanterna. Clausius-Clapeyrons ekvation innehåller två konstanter: R och ΔHvap. R är alltid lika med 8,314 J/(K × Mol). Hvap (avdunstningens entalpi), men det beror på vilket ämne du undersöker ångtrycket för. Som nämnts ovan kan du använda ΔHvap hitta värden för ett stort antal ämnen på baksidan av kemi- eller fysikböcker, eller möjligen online (som till exempel, här.)

4. Lös ekvationen. När alla variabler har matats in i ekvationen (förutom variabeln du vill lösa), fortsätt att lösa ekvationen enligt vanliga algebraregler.
Metod 2 av 3: Bestämning av ångtrycket med lösningar

1. Skriv ner Raoults lag. I verkliga livet är det sällsynt att du har att göra med en enda ren lösning - vanligtvis har du att göra med vätskor som är blandningar av olika föreningar. Några av de mest kända av dessa blandningar görs genom att lösa upp en liten mängd av en viss kemikalie som kallas ämne som ska lösas upp i en stor mängd av ett ämne, det lösningsmedel (eller lösningsmedel) till a lösning I dessa fall är det användbart att ha kunskap om en ekvation som kallas Raoults lag (efter fysikern François-Marie Raoult), som ser ut så här: sidlösning=PlösningsmedelXlösningsmedel. I denna formel hänvisar variablerna till:
- sidlösning: Ångtrycket för den kompletta lösningen (alla kombinerade beståndsdelar)
- sidlösningsmedel: Lösningsmedelsångtryck
- Xlösningsmedel: Molfraktionen av lösningsmedlet.
- Oroa dig inte om du använder termer som "molfraktion" vet inte – vi kommer att förklara det i de kommande stegen.

2. Identifiera lösningsmedlet och det lösta ämnet i din lösning. Innan du kan beräkna ångtrycket för en sammansatt vätska måste du analysera de ämnen du arbetar med. Som en påminnelse bildas en lösning när ett ämne löses i ett lösningsmedel - kemikalien som löser sig är alltid det lösta ämnet och kemikalien som löser sig är alltid lösningsmedlet.

3. Bestäm temperaturen på lösningen. Som vi såg i avsnittet Clausius Clapeyron ovan kommer temperaturen på en vätska att påverka dess ångtryck. Generellt gäller att ju högre temperatur desto högre ångtryck - när temperaturen ökar kommer mer av vätskan att förångas, vilket ökar ångtrycket i det slutna utrymmet.

4. Bestäm lösningsmedlets ångtryck. Kemiska referensmaterial har vanligtvis ångtrycksvärden för många vanliga ämnen och föreningar, men dessa gäller vanligtvis endast vid temperaturer på 25°C/298K eller vid kokpunkten. Om temperaturen på lösningen har ett av dessa värden kan du använda referensvärdet; om inte måste du hitta ångtrycket vid den aktuella temperaturen.

5. Bestäm molfraktionen av lösningsmedlet. Det sista vi behöver göra innan vi kan lösa är att bestämma molfraktionen av lösningsmedlet. Att hitta molfraktioner är väldigt enkelt: omvandla bara komponenterna till mol, och hitta sedan procentandelen av de totala molerna i ämnet som varje komponent upptar. Med andra ord är molfraktionen av varje komponent lika med (antal mol av komponent) / (totalt antal mol av ämnet).

6. Lösa. Nu har vi äntligen allt vi behöver för att lösa ekvationen av Raoults lag. Den här delen är förvånansvärt enkel: ersätt värdena med variablerna i den förenklade ekvationen av Raoults lag i början av detta avsnitt (sidlösning = PlösningsmedelXlösningsmedel).
Metod 3 av 3: Bestäm ångtrycket i speciella fall

1. Var medveten om standardtemperatur- och tryckförhållandena. Forskare använder ofta ett antal fasta värden för temperatur och tryck, som en slags praktisk "standard". Dessa värden kallas standardtemperatur och tryck (standardförhållandena). Ångtrycksangivelser använder ofta standardvillkor, så det är bra att memorera dessa värden. Standardtemperaturen och -trycket definieras som:
- Temperatur: 273,15 K / 0 C / 32 F
- Upptagen: 760 mm Hg / 1 atm / 101 325 kilopascal

2. Ordna Clausius-Clapeyrons ekvation för att hitta andra variabler. I vårt exempel i del 1 såg vi att Clausius-Clapeyron-ekvationen är mycket användbar för att hitta ångtrycket för rena ämnen. Men inte alla frågor kommer att handla om att bestämma P1 eller P2 - i många fall kommer du att bli ombedd att hitta ett temperaturvärde, eller ibland till och med ett ΔHvap där den. Lyckligtvis är att bestämma det korrekta svaret i dessa fall ofta inte mer än en fråga om att skriva om ekvationen så att variabeln du löser för är isolerad på ena sidan av likhetstecknet.

3. Tänk på ångtrycket hos det lösta ämnet när det producerar ånga. Med exemplet på Raoults lag ovan, producerar det lösta ämnet, socker, inte själv ånga vid normala temperaturer (när såg du senast en skål med socker avdunsta??) Men när det lösta ämnet inte avdunstar, kommer det att påverka ångtrycket. Vi kan visa detta med en modifierad version av Raoults lag: sidlösning = Σ(PkomponentXkomponent) Sigma-symbolen (Σ) betyder att vi måste lägga ihop ångtrycken för alla komponenter för att hitta svaren.
Tips
- För att använda Clausius Clapeyrons ekvation ovan måste temperaturen mätas i Kelvin (betecknad som K). Om temperaturen anges i grader Celsius, måste du konvertera den med följande formel: tk = 273 + Tc
- Ovanstående metoder fungerar eftersom energin är direkt proportionell mot mängden tillförd värme. Vätskans temperatur är den enda miljöfaktor som ångtrycket beror på.
Оцените, пожалуйста статью