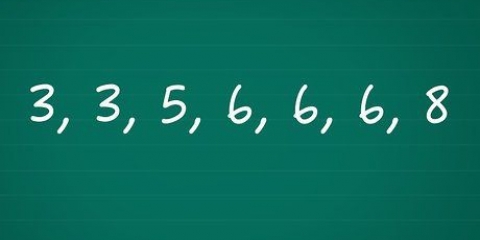Låt oss fortsätta att arbeta med exemplet ovan. Här är vår datauppsättning som visar temperaturerna i grader Fahrenheit för olika objekt i ett rum: {71, 70, 73, 70, 70, 69, 70, 72, 71, 300, 71, 69}. Om vi sorterar värdena i mängden från lägsta till högsta blir detta vår nya uppsättning: {69, 69, 70, 70, 70, 70, 71, 71, 71, 72, 73, 300}. 
Bli inte förvirrad av datamängder med ett jämnt antal poäng - medelvärdet av de två mittpunkten är ofta ett tal som inte finns i själva datasetet - det här är okej. Men om de två mittpunkterna är lika, kommer medelvärdet givetvis också att vara detta tal - det är också detta Okej. I vårt exempel har vi 12 poäng. De två mittersta termerna är punkterna 6 och 7 – 70 respektive 71. Så medianen för vår datamängd är medelvärdet av dessa två punkter: ((70 + 71) / 2)=70,5. 
I vårt exempel ligger sex punkter över medianen och sex under den. Så för att hitta den första kvartilen måste vi ta medelvärdet av de två mittpunkten i de sex nedersta punkterna. Punkterna 3 och 4 av de sex nedersta är båda 70, så deras medelvärde är ((70 + 70) / 2)=70. Så vårt värde för Q1 är 70. 
Om vi fortsätter med exemplet ovan ser vi att de två mittpunkterna av de sex punkterna ovanför medianen är 71 och 72. Medelvärdet av dessa två punkter är ((71 + 72) / 2)=71,5. Så vårt värde för Q3 är 71,5. 
I vårt exempel är värdena för Q1 och Q3 70 respektive 71,5 . För att hitta interkvartilintervallet beräknar vi Q3 - Q1: 71,5 - 70=1,5. Detta fungerar även om Q1, Q3 eller båda siffrorna är negativa. Till exempel, om vårt värde för Q1 var -70, skulle interkvartilintervallet vara 71,5 - (-70)=141,5, vilket är korrekt. 
I vårt exempel är interkvartilintervallet (71,5 - 70), eller 1,5. Multiplicera detta med 1,5 och du får 2,25. Vi adderar detta tal till Q3 och subtraherar det från Q1, för att hitta de inre gränserna enligt följande: 71,5 + 2,25=73,75 70 - 2,25=67,75 Så är de inre gränserna 67,75 och 73,75. I vår datauppsättning är endast ugnstemperaturen – 300 grader Fahrenheit – utanför detta intervall. Så detta kan vara en mild avvikelse. Men vi har också ännu inte avgjort om denna temperatur är en extrem extremvärde, så låt oss inte dra några slutsatser ännu.

I vårt exempel multiplicerar vi interkvartilintervallet med 3, och vi kommer fram till (1,5 *3) eller 4,5. Vi kan nu hitta de yttre gränserna på samma sätt som de inre gränserna: 71,5 + 4,5=76 70 - 4,5=65,5 Så de yttre gränserna är 65,5 och 76. Datapunkter som ligger utanför de yttre gränserna anses vara extrema extremvärden. I vårt exempel ligger ugnstemperaturen, 300 grader Fahrenheit, långt utanför de yttre gränserna. Så ugnstemperaturen är säkra en extrem utstickare.

Ett annat kriterium att överväga är om extremvärdena påverkar medelvärdet av en datamängd på ett sätt som är snedvridet eller missvisande. Detta är särskilt viktigt om du tänker dra slutsatser från genomsnittet av din datamängd. Låt oss granska vårt exempel. Sedan det i hög grad Även om det är osannolikt att ugnen nådde en temperatur på 300°F på grund av någon oförutsedd naturkraft, kan vi i vårt exempel dra slutsatsen med nästan 100 % säkerhet att ugnen lämnades påslagen av misstag, vilket resulterade i en onormalt hög temperaturavläsning. Dessutom, om vi inte tar bort extremvärdet blir vår datamängd i genomsnitt (69 + 69 + 70 + 70 + 70 + 70 + 71 + 71 + 71 + 72 + 73 + 300)/12=89,67 °F, medan genomsnittet utan extremvärdet kommer ut vid (69 + 69 + 70 + 70 + 70 + 70 + 71 + 71 + 71 + 72 + 73)/11=70,55 °F. Eftersom avvikelsen orsakades av mänskliga fel, och eftersom det är felaktigt att säga att den genomsnittliga rumstemperaturen var nära 32°C, måste vi välja att välja vårt yttervärde avlägsna. 
Tänk dig till exempel att vi designar ett nytt läkemedel för att få fisk att växa sig större i en fiskodling. Låt oss använda vår gamla datamängd ({71, 70, 73, 70, 70, 69, 70, 72, 71, 300, 71, 69}), förutom att varje punkt nu representerar massan av en fisk (i gram) efter behandling med ett annat experimentellt läkemedel från födseln. Med andra ord, det första läkemedlet gav en fisk en massa på 71 gram, det andra gav en annan fisk en massa på 70 gram, och så vidare. I den här situationen 300 . är fortfarande en enorm avvikare, men vi borde inte ta bort den nu. För om vi antar att extremvärdet inte är resultatet av ett fel, representerar det en stor framgång i vårt experiment. Läkemedlet som producerade en 300 grams fisk fungerade bättre än något annat läkemedel, så det här är det mest viktig datapunkt i vår uppsättning, snarare än minst viktig datapunkt.
Beräkna extremvärden
A uteliggare eller uteliggare i statistik, en datapunkt som skiljer sig signifikant från de andra datapunkterna i ett urval. Ofta påpekar extremvärden för statistiker anomalier eller fel i mätningarna, varefter de kan ta bort extremvärdet från datamängden. Om de faktiskt väljer att ta bort extremvärdena från datamängden kan det medföra betydande förändringar i slutsatserna från studien. Det är därför det är viktigt att beräkna och fastställa extremvärden om man vill tolka statistiska data korrekt.
Steg

1. Lär dig hur du upptäcker potentiella extremvärden. Innan vi kan bestämma om vi ska ta bort avvikande värden från en viss datamängd måste vi naturligtvis känna igen de möjliga extremvärdena i datamängden. I allmänhet är extremvärden de datapunkter som avviker avsevärt från trenden att de andra värdena i uppsättningsformen – med andra ord, de skjuta ut av de andra värdena. Det är vanligtvis lätt att känna igen detta i tabeller och (särskilt) i grafer. Om datamängden grafiseras visuellt kommer extremvärdena att vara "långt borta" från de andra värdena. Till exempel, om de flesta punkter i en datamängd bildar en rät linje, kommer extremvärden inte att överensstämma med denna linje.
- Låt oss titta på en datauppsättning som visar temperaturerna för 12 olika föremål i ett rum. Om temperaturen på 11 av objekten fluktuerar runt 21°C med högst några grader, medan ett föremål, en ugn, har en temperatur på 150°C, kan man med en blick se att ugnen troligen är en utstickare.

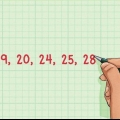
2. Sortera alla datapunkter från låg till hög. Det första steget i att beräkna extremvärden är att hitta medianvärdet (eller mittvärdet) för datamängden. Denna uppgift blir mycket lättare om värdena i uppsättningen är i ordning från lägsta till högsta. Så innan du fortsätter, sortera värdena i din datauppsättning så här.

3. Beräkna medianen för datamängden. Medianen för en datamängd är den datapunkt där hälften av datan ligger ovanför den och hälften av datan ligger under - det är i princip "centrum" av datamängden. Om datamängden innehåller ett udda antal punkter är medianen lätt att hitta – medianen är punkten med lika många punkter ovanför som under den. Om det finns ett jämnt antal poäng, eftersom det inte finns en mittpunkt, måste du ta medelvärdet av de två mittpunkterna för att hitta medianen. Vid beräkning av extremvärden betecknas medianen vanligtvis med variabeln Q2 – eftersom den ligger mellan Q1 och Q3, första och tredje kvartilen. Vi kommer att bestämma dessa variabler senare.

4. Beräkna den första kvartilen. Denna punkt, som vi kallar variabeln Q1, är den datapunkt under vilken 25 procent (eller en fjärdedel) av observationerna ligger. Med andra ord, detta är mittpunkten för alla punkter i din datauppsättning Nedan medianen. Om det finns ett jämnt antal värden under medianen, måste du återigen genomsnittet av de två mittenvärdena för att hitta Q1, vilket du kanske redan har gjort för att bestämma medianen själv.

5. Beräkna den tredje kvartilen. Denna punkt, som vi betecknar med variabeln Q3, är den datapunkt över vilken 25 procent av datan ligger. Att hitta Q3 är praktiskt taget detsamma som att hitta Q1, förutom i det här fallet tittar vi på punkterna ovan medianen.

6. Hitta det interkvartila området. Nu när vi har bestämt Q1 och Q3 måste vi beräkna avståndet mellan dessa två variabler. Avståndet mellan Q1 och Q3 kan hittas genom att subtrahera Q1 från Q3. Värdet du får för det interkvartila intervallet är avgörande för att bestämma gränserna för icke-avvikande punkter i din datamängd.

7. Hitta de "inre gränserna" för datamängden. Du kan identifiera extremvärden genom att avgöra om de faller inom ett antal numeriska gränser; de så kallade "inre gränsvärdena" och "yttre gränsvärden". En punkt som faller utanför de inre gränserna för datamängden klassificeras som en mild avvikelse, och en punkt som faller utanför de yttre gränserna klassificeras som en extrem utstickare. För att hitta de inre gränserna för din datamängd, multiplicera först det interkvartila intervallet med 1,5. Lägg till resultatet till Q3 och subtrahera det från Q1. De två resultaten är de inre gränserna för din datamängd.


8. Hitta de "yttre gränserna" för datamängden. Du gör detta på samma sätt som med de inre gränserna, med den enda skillnaden att du multiplicerar interkvartilområdet med 3 istället för med 1,5. Du lägger sedan till resultatet till Q3 och subtraherar från Q1 för att hitta de yttre gränserna.


9. Använd en kvalitativ bedömning för att avgöra om du ska "kassera" extremvärdena. Med metoden ovan kan du avgöra om vissa punkter är milda extremvärden, extrema extremvärden eller inga extremvärden alls. Men gör inga misstag – att erkänna en punkt som en extremist gör den bara till en kandidat ska tas bort från datamängden och inte omedelbart en prick borttagen måste bli till. De red varför en outlier skiljer sig från resten av punkterna i setet är avgörande för att avgöra om outlier ska tas bort. I allmänhet tas extremvärden som orsakats av något fel - ett fel i mätningarna, i inspelningarna eller i den experimentella designen, till exempel - bort. Däremot är extremvärden som inte orsakas av fel och som avslöjar ny, oförutsedd information eller trender vanligtvis inte raderade.

10. Förstå vikten av att (ibland) behålla extremvärden. Även om vissa extremvärden bör tas bort från en datamängd eftersom de är resultatet av fel eller för att de vilseledande förvränger resultaten, bör andra extremvärden bevaras. Till exempel, om en extremvärde har erhållits korrekt (dvs. inte resultatet av ett fel) och/eller om extremvärdet ger en ny insikt om fenomenet som ska mätas, bör det inte tas bort omedelbart. Vetenskapliga experiment är särskilt känsliga situationer när det kommer till att hantera extremvärden – att felaktigt ta bort en extremvärde kan innebära att man kastar bort viktig information om en ny trend eller upptäckt.
Tips
- Om du hittar extremvärden, försök att förklara dem innan du tar bort dem från datamängden; de kan indikera mätfel eller avvikelser i fördelningen.
Förnödenheter
- Kalkylator
Оцените, пожалуйста статью