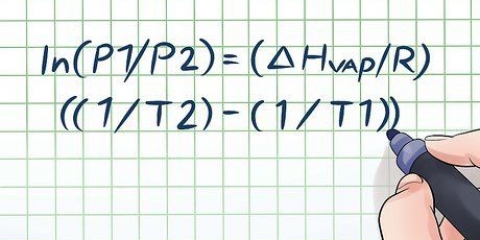Loggen för ett tal med en given bas är exponenten med vilken basen ökas (eller antalet gånger basen multipliceras med sig själv) för att få det talet. Loggen har bas 10. Loggknappen på din miniräknare är en vanlig logaritm. Om du beräknar att log (1,5) = 0,176, dam betyder det att log på 1,5 är lika med 0,176. Detta betyder återigen att 10 till 0,176-potentialen är lika med 1,5. 
Till exempel, om den förflutna tiden är lika med 100 minuter, multiplicera 100 med 0,30103. Detta resultat är lika med 30,103. 
Så, 30,103 / 0,176 = 171,04. Detta är halveringstiden för ämnet uttryckt i tidsenheten för det tredje steget. 
Så,ln( 1,5) = 0,405 och ln(2) = 0,693. Sedan följer: 0,693 x 100 = 69,3. Dividera detta tal med 0,405 och du får 171,04, samma svar som med den vanliga loggen. Lös detta fram och bak. Om 12,5 gram av ämnet återstod fanns det före halveringen 25 g av ämnet (12,5 x 2); innan dess fanns det 50 g av ämnet; där igen för 100 g, och du började med 200 g. Så ämnet fick halveras 4 gånger för att komma från 200 g till 12,5 g, så man kan räkna ut att halveringstiden är lika med 24 timmar/4 = 6 timmar. Börja med 20 g och reducera den. 20/2 = 10 (1 halvering), 10/2 = 5 (2 halvingar), 5/2 = 2,5 (3 halvingar) och 2,5/2 = 1,25 (4 halvingar). Svaret är 4 halvor.
Beräkna halveringstiden för ett ämne
Halveringstiden eller halveringstiden för ett ämne som sönderfaller över tid är den tid det tar för en given mängd av ämnet att sönderfalla till hälften. I princip var denna term reserverad för radioaktivt sönderfall av grundämnen som uran eller plutonium, men den kan också användas för vilket ämne som helst som är föremål för sönderfall, i linjär eller exponentiell hastighet. Du kan beräkna halveringstiden för vilket ämne som helst, förutsatt att sönderfallshastigheten anges. Detta är mängden av ämnet du börjar med och mängden som finns kvar efter en viss tid. Läs vidare för att lära dig hur man beräknar halveringstiden för ett ämne.
Steg
Del 1 av 2: Beräkna halveringstiden

1. Dela mängden av ett ämne vid varje given tidpunkt med mängden som blir över efter en viss tidsperiod.
- Formeln för att beräkna halveringstiden ser ut så här: t1/2 = t * ln(2)/ln(N0/Nt)
- I denna formel ser vi följande variabler: t = förfluten tid, N0 = mängden av ett ämne för mätningen och Nt = mängd av ett ämne efter en viss tidsperiod.
- Till exempel, om mängden du börjar med är 1500 gram och slutmängden är 1000 gram, då är 1500 / 1000 = 1,5. Vi säger att tiden som förflutit är lika med (t) = 100 minuter.

2. Beräkna logaritmen (log) för talet från föregående steg. Allt du behöver göra nu är att skriva log(1,5) på din miniräknare.

3. Multiplicera den förflutna tiden med log(2). Log(2) = 0,30103. Den förflutna tiden är 100 minuter.

4. Dela resultatet av föregående beräkning med siffran från det andra steget.

5. Färdiga. Nu när du har hittat halveringstiden för detta exempel är det bra att veta att du kunde ha använt den naturliga logaritmen (ln) istället för den vanliga loggen för att få samma resultat. Faktum är att den naturliga logaritmen oftare används för att hitta halveringstiden än den vanliga logaritmen.
Del 2 av 2: Lösa problem med halveringstid
1. Bestäm hur mycket av ett ämne med känd halveringstid som finns kvar efter en given mängd dagar. Lösa: Om 20 mg jod-131 ges till en patient, hur mycket är kvar efter 32 dagar? Halveringstiden för jod-131 är 8 dagar. Så här gör du:
- Bestäm hur mycket av ämnet som halveras på 32 dagar. För att göra detta, dividera 32 med 8 (substanshalveringstid). 32/8 = 4, så tyget halveras 4 gånger.
- Det betyder att du efter 8 dagar fortfarande har 20mg/2, eller 10mg av ämnet; efter 16 dagar är detta fortfarande 10 mg/2 eller 5 mg; efter 24 dagar har du 5 mg/2, eller 2,5 mg kvar och efter 32 dagar finns det fortfarande 2,5 mg/2, eller 1,25 mg kvar av ämnet.
2. Bestäm halveringstiden för ett visst ämne, känna till start- och slutmängden samt den förflutna tiden. Lös följande problem: Om ett labb tar emot en leverans av 200 g teknetium-99m och bara 12,5 g av isotopen återstår, vad är halveringstiden för teknetium-99m? Så här gör du:
3. Frågan är hur många halveringar som behövs för att minska ett ämne till en viss mängd. Lös följande: Om halveringstiden för uran-232 är 70 år, hur många halveringar behövs för att minska 20 g av ämnet till 1,25 g? Här är effekten:
Varningar
- Halveringstid är en uppskattning (av en slump) av den tid som krävs för att hälften av ämnet ska sönderfalla, snarare än en exakt beräkning. Till exempel, om det bara finns en atom av ett visst ämne kvar, är halvering inte längre möjlig (eller 1 eller 0 atomer kvarstår). Ju större mängd rester, desto mer exakt är halveringstiden, eftersom du har att göra med lagen om stora siffror.
Förnödenheter
- Kalkylator
"Beräkna halveringstiden för ett ämne"
Оцените, пожалуйста статью