Inte ens π-knappen på en miniräknare använder det exakta värdet av π, även om den är tillräckligt korrekt. 
C är bara ett kortare sätt att skriva `omkrets`. 
Du kanske har skrivit vänster sida som π2r, vilket också är korrekt. Folk gillar att sätta siffrorna före symbolerna för att göra ekvationen lättare att läsa, men det ändrar inte resultatet av ekvationen. I en matematisk ekvation kan du alltid multiplicera vänster och höger sida med samma mängd och ändå få en korrekt ekvation. 
Till exempel, om radien är två enheter lång, då är 2πr = 2 x (3,14) x (2 enheter) = 12,56 enheter = omkretsen. I samma exempel, men med hjälp av π-knappen på en miniräknare för bättre noggrannhet, får du 2 x π x 2 enheter = 12,56637... enheter, men om inte din lärare instruerar något annat kan du avrunda antalet till 12,57 enheter. 

Vi använder d`, inte2r, eftersom ditt matematiska problem säger dig vad d betyder att. Det är dock viktigt att förstå detta steg så att du inte blir förvirrad om din lärare eller mattebok 2r används där du har en d skulle förvänta sig. 
Inte ens π-knappen på en miniräknare använder det exakta värdet av π, även om det är mycket exakt. 

π x d = (C/d) x d πd = C 
Till exempel, om diametern är sex, får du (3,14) x (6) = 18,84. I samma exempel, men med hjälp av en miniräknares π-knapp för mer noggrannhet, får du π x 6 = 18,84956... men om inget annat anges kan du avrunda siffran till 18,85. 


A = r A / π = πr / π = r √(A/π) = √(r) = r r = √(A/π) 
C = 2πr C = 2π(√(A/π)) 
Svaret för detta exempel är 13.72937... men om inget annat anges kan du avrunda svaret till 13,73. 


Se till att du virar snöret runt det mer än en gång. Du bör sluta med en enda slinga så att det inte finns någon del av cirkeln där repet är dubbellindat. 

Hitta en cirkels omkrets
En cirkels omkrets är avståndet runt dess kant. Om en cirkel har en omkrets på 2 miles, måste du gå runt cirkeln 2 miles innan du återvänder till där du började. Men om du arbetar med ett geometriskt problem behöver du inte gå upp ur stolen. Läs problemet noga för att ta reda på om cirkelns `radie` (r), `diameter` (d) eller `area` (A) av cirkeln är given, och hitta sedan den del av den här artikeln som är avsedd att hjälpa dig med uppgiften. Det finns också instruktioner för att hitta omkretsen av ett befintligt cirkulärt objekt som du vill mäta.
Steg
Metod 1 av 4: Bestämning av omkretsen med hjälp av radien

1. Rita en "stråle" på cirkeln. Rita en linje från mitten av cirkeln till valfri position på kanten av cirkeln. Denna linje är cirkelns "radie", ofta skriven som "r" i matematiska ekvationer och formler.
- `Anmärkning: om radien inte anges i matematikuppgiften kan det hända att dessa inte är de korrekta instruktionerna. Se om de om diametern eller ytan är mer användbara för uppdraget.

2. Rita en `diameter` över cirkeln. Förläng linjen du precis ritade så att den når cirkelkanten på andra sidan. Du ritade precis en andra stråle. De två tillagda radierna har en längd på `2 x radien`, skrivna som 2r. Längden på denna linje är "diametern" på cirkeln, ofta skriven som d.

3. Förstå π (`pi`). Symbolen π, även skrivet som pi är inte ett magiskt tal som råkar användas i den här typen av matematiska problem. Faktum är att talet π ursprungligen `upptäcktes` genom att mäta cirklar: om du mäter omkretsen av en cirkel (till exempel med ett måttband) och sedan dividerar med diametern, får du alltid samma siffra. Detta nummer är ovanligt eftersom det inte kan skrivas som en enkel bråkdel eller decimal. Istället kan vi avrunda det till ett tal som 3,14, vilket är "tillräckligt bra".

4. Skriv definitionen av π som ett algebraproblem. Som förklarats ovan betyder π bara "talet du får när du dividerar omkretsen med diametern". I form av en matematisk formel är detta: π = C/d. Eftersom vi vet att diametern är lika med 2 x radien kan vi också skriva detta som π = C/2r.

5. Ändra detta problem så att du löser det här problemet för omkretsen C. Vi vill veta vad omkretsen är (C i detta matematiska problem). Om du multiplicerar båda sidor med 2r du får π x 2r = (C / 2r) x 2r, och det är samma sak som 2πr = C.

6. Byt ut talen för att lösa C. Nu vet vi det 2πr = C. Gå tillbaka till det ursprungliga matematiska problemet för att se vad r (radien) är. Ersätt sedan π med 3,14, eller använd π-knappen på din miniräknare för att få ett mer exakt svar. Beräkna 2πr med dessa tal. Svaret du får är omkretsen.
Metod 2 av 4: Bestäm omkretsen med hjälp av diametern

1. Förstå vad en "diameter" är. Placera din penna på kanten av cirkeln. Rita en linje genom mitten av cirkeln och kanten på andra sidan. Denna linje (från kant till kant och genom mitten) är "diametern" på cirkeln, ofta skriven som d i matteproblem.
- Linjen går genom cirkelns exakta mitt, inte var som helst i cirkeln.
- Anmärkning: Om påståendet inte anger hur lång diametern är, använd en annan metod.

2. Lär dig vad d = 2r betyder. Cirkelns `radie`, även skriven som r, är avståndet från mitten till cirkelns kant. Eftersom diametern går genom cirkeln från kant till kant, genom mitten, är diametern lika med två radier. Ett enkelt sätt att skriva detta är d = 2r. Det betyder att du d kan alltid ersätta med 2r i ett matematiskt problem och vice versa.

3. Förstå π (`pi`). Symbolen π, även skrivet som pi är inte ett magiskt tal som råkar användas i den här typen av matematiska problem. Faktum är att talet π ursprungligen `upptäcktes` genom att mäta cirklar: om du mäter omkretsen av en cirkel (till exempel med ett måttband) och sedan dividerar med diametern, får du alltid samma siffra. Detta nummer är ovanligt eftersom det inte kan skrivas som en enkel bråkdel eller decimal. Istället kan vi avrunda det till ett tal som 3,14, vilket är "tillräckligt bra".

4. Skriv definitionen av π som ett algebraproblem. Som förklarats ovan betyder π bara "talet du får när du dividerar omkretsen med diametern". I form av en matematisk formel är detta: π = omkrets / diameter eller π = C/d.

5. Ändra detta problem så att du löser det här problemet för omkretsen C. Vi vill veta vad omkretsen är, så vi behöver bara få C på ena sidan. Gör detta genom att multiplicera varje sida av ekvationen med d:

6. Byt ut talen och lös C. Återgå till det ursprungliga problemet för att se vad diametern är och ersätt d:et i denna ekvation med det numret. Ersätt π med en avrundning som 3,14, eller använd π-knappen på din miniräknare för ett mer exakt resultat. Multiplicera värdena och d tillsammans så får du omkretsen C.
Metod 3 av 4: Hitta omkretsen med hjälp av området

1. Förstå hur arean av en cirkel beräknas. Vanligtvis området (a) av en cirkel som inte mäts direkt. Istället mäter du radien (r) av cirkeln och beräkna sedan arean med formeln A = r. Anledningen till att den här formeln är vettig är lite svår att förklara, men du kan lära dig mer genom denna länk om du är intresserad och villig att gå till botten med någon tyngre algebra.
- Anmärkning: Om det matematiska problemet inte nämner cirkelns yta kan du behöva använda en annan metod än den här artikeln.

2. Lär dig en formel för att beräkna omkrets. omkretsen (C) är avståndet runt cirkeln. Du beräknar vanligtvis detta med formeln C=2πr, men eftersom vi inte vet ännu vad radien (r), måste vi lägga lite tid på att räkna ut värdet på r innan vi kan lösa ekvationen.

3. Använd areaformeln för att få r på ena sidan. Eftersom A = πr kan vi ordna om denna formel för att lösa r istället. Om du tycker att stegen nedan är svåra att följa, kanske du vill prova några enklare algebraproblem först eller öva på några tekniker för att förstå algebra.

4. Ändra omkretsformeln med det du hittade. Varje gång du har en ekvation som r = √(A/π), kan du ersätta ena sidan av ekvationen med den andra?. Låt oss använda den här tekniken för att få ovanstående omkretsformel, C=2πr, att förändra. För det här problemet vet vi inte värdet på r, men vi vet det för A. Låt oss ändra det så här för att göra problemet lösbart:

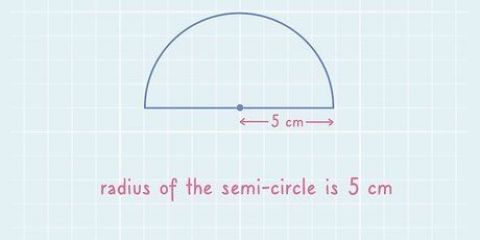
5. Byt ut siffrorna för att hitta omkretsen. Använd området som anges i uppgiften för att hitta omkretsen av omkretsen. Till exempel, om området (a) av en cirkel är 15 kvadratenheter, fyll sedan i 2π(√(15/π)) i din miniräknare. Glöm inte fästena.
Metod 4 av 4: Bestämma omkretsen av en verklig cirkel

1. Använd den här metoden för att mäta verkliga cirkulära objekt. Du kan mäta omkretsen av cirklar du hittar i den verkliga världen, inte bara i problem. Prova på ett cykelhjul, en pizza eller ett mynt.

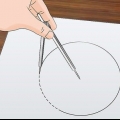
2. Ta en bit snöre och en linjal. Snöret ska vara tillräckligt långt för att linda cirkeln en gång och tillräckligt flexibelt för att passa tätt. Du kommer att behöva något för att mäta repet senare, till exempel en linjal eller måttband. Snöret blir lättare att mäta om linjalen är längre än strängen.

3. Linda snöret en gång runt cirkeln. Börja med att placera ena änden av snöret längs kanten på cirkeln. Dra repet runt cirkeln och dra åt det. Om du mäter ett mynt eller annat tunt föremål kanske du inte kan dra snöret hårt runt det. Lägg det cirkulära föremålet plant och arrangera snöret runt det, så hårt som möjligt.

4. Markera eller klipp av snöret. Hitta platsen på snöret där öglan slutar och rör vid slutet av snöret du började med. Markera denna plats med en markör, eller klipp av repet på denna plats.

5. Lossa repet och mät det med en linjal. Ta det lindade repet och mät det med en linjal. Om du använde en markör, mät endast från slutet av snöret till markören. Detta är den del av strängen som sveper runt cirkeln, och eftersom omkretsen av en cirkel bara är avståndet runt cirkeln, har du hittat svaret! Längden på detta rep är lika med cirkelns omkrets.
Tips
- Du kan skriva pluralis av radie som radier eller som radier.
Оцените, пожалуйста статью