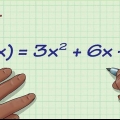Om värdet av a är positivt, då får du minimivärdet, eftersom parabeln överst är öppen (punkten är den lägsta punkten på grafen).
Om värdet av a är negativ, hittar du det maximala värdet, eftersom parabeln längst ner är öppen (punkten är den högsta punkten på grafen).
Värdet av a kan inte vara noll, annars har vi inte att göra med en andragradsekvation, eller hur?







Bestämma maximi- och minimivärdena för en kvadratisk funktion
Y-koordinaten för en parabels krön eller dal (vanligtvis representerad av k) är också det maximala eller lägsta värdet för andragradsekvationen som representeras av parabeln. Låt oss se hur man bestämmer det!
Steg
Metod 1 av 4: För en andragradsekvation av formen y = ax + bx + c

1. Bestäm om du vill bestämma maxvärdet eller minimivärdet. Det är det ena eller det andra, du kan inte göra båda.
- Det maximala eller lägsta värdet för en andragradsekvation är detsamma som toppen eller dalen för den funktionen.
Funktionen y = ax + bx + c,
(c - b/4a) returnerar y-värdet (värdet av funktionen) som vertex.




Metod 2 av 4: För en andragradsekvation i formen y = a(x-h) + k

1. För y = a(x-h) + k, k är värdet på funktionen vid vertex.
- k ger oss det högsta eller lägsta värdet av andragradsekvationen när a är negativ respektive positiv.

Metod 3 av 4: Differentiera på en andragradsekvation av formen y = ax^2 + bx + c

1. Differentiera y för x. dy/dx = 2ax + b

2. Bestäm vad de härledda värdena är i termer av dy/dx. Eftersom dy/dx är derivatans funktion av en kurva, kan derivatan av en kurva bestämmas när som helst. Det maximala/minsta värdet kan därför bestämmas genom att sätta dessa värden lika med 0, och sedan bestämma motsvarande värden. dy/dx = 0, 2ax+b = 0, x = -b/2a

3. Byt ut minimi-/maximivärdet med detta värde på x med y.
Metod 4 av 4: Exempel

1. Bestäm det högsta eller lägsta värdet för funktionen f(x) = x + x + 1.

2. Bestäm det högsta eller lägsta värdet för funktionen f(x) = -2(x-1) + 3.
Tips
- Parabolens symmetriaxel är x = h.
- -h är det värde som motsvarar max- eller minimivärdet.
"Bestämma maximi- och minimivärdena för en kvadratisk funktion"
Оцените, пожалуйста статью