Om du vill beräkna arean av en kvadrat kan du spara tid genom att använda en miniräknare och kvadrera en sida. Så om en sida är fyra meter, klicka på 4 och sedan på den fyrkantiga knappen på din miniräknare för att få svaret. Kvadring multiplicerar ett tal med sig själv. 
Detta kallas också för cm i kvadrat, eller skrivet med en liten "2" uppe till höger på enheten, istället för ordet "kvadrat". 


























Bestämma arean av en form
Det finns många olika former och lika många anledningar till varför du skulle vilja veta deras yta! Oavsett om du gör dina läxor eller försöker ta reda på hur mycket färg du behöver för att måla om ditt vardagsrum, kan wikiHow hjälpa! Börja bara med steg 1 nedan för att lära dig hur man beräknar arean av en form.
Steg
Metod 1 av 7: kvadrater, rektanglar och parallellogram

1. Mät bredd och höjd. Börja med att bestämma formens bredd och höjd (med andra ord genom att bestämma längden på två intilliggande sidor).
- För ett parallellogram behöver du basen och den vertikala höjden, men de är desamma som bredden och höjden.
- I den verkliga världen måste du mäta detta själv, men för dina läxor kommer dessa mått att ges tillsammans med formen.

2. Multiplicera sidorna. Multiplicera sidorna tillsammans. Till exempel, om du har en rektangel med en höjd på 16 cm och en bredd på 42 cm, multiplicera 16 x 42.

3. Bestäm resultatet. Det resulterande talet från multiplikationen är arean av din form, skrivet som "kvadratenheter". Så arean av vår rektangel är 672 kvadrat cm.
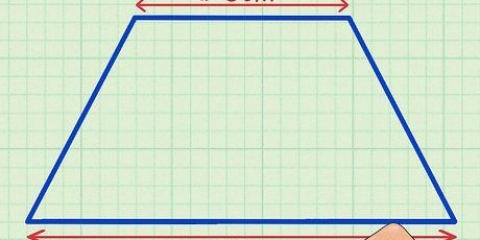
Metod 2 av 7: Trapets

1. Ta dina mått. Du behöver måtten från basen, toppen och den vertikala höjden. Basen och toppen är parallella, medan höjden mäts längs en av sidorna med vinkeln.
- I den verkliga världen måste du mäta detta själv, men för dina läxor kommer dessa mått att ges tillsammans med formen.

2. Lägg till längden på höjden och basen tillsammans. Anta att höjden är 5 cm och basen är 7 cm. Detta ger oss ett värde på 12.

3. Multiplicera det värdet med 1/2. detta ger oss ett värde på 6.

4. Multiplicera det värdet med höjden. Anta att vi har en trapets på 6 cm. Detta ger oss ett värde på 36.

5. Bestäm resultatet. Det resulterande talet efter multiplicering med höjden är trapetsens area. Så med en trapets på 5 x 6 x 7 är arean 36 cm.
Metod 3 av 7: Cirkel

1. Bestäm radien. För att hitta arean av en cirkel måste du känna till dess radie. Detta är avståndet från cirkelns mitt till kanten. Du kan också bestämma detta med diametern, eller bredden på cirkeln, varefter du delar den med två.
- I den verkliga världen måste du mäta detta själv, men för dina läxor kommer dessa mått att ges tillsammans med formen.

2. Kvadra radien. Multiplicera radien med sig själv. Anta att vi har en radie på 8 meter, detta ger oss ett värde på 64.

3. Multiplicera med pi. Pi (π) är ett tal med många decimaler och används i många beräkningar. Om du använder en miniräknare, använd pi-funktionen för ett mycket exakt resultat. Om inte kan du avrunda pi (ignorera de flesta decimalerna) till 3,14159. Detta ger oss en produkt efter att ha multiplicerat 201,06176.

4. Bestäm resultatet. Det resulterande numret (201.06176 i det här fallet) är cirkelns yta. Så vi får ett resultat på 201,06176 m.
Metod 4 av 7: Segment

1. Bestäm måtten. Segment är delar av en cirkel som ser ut som fans. Du mäter radien för den ursprungliga cirkeln, eller ena sidan av din "fläkt", såväl som vinkeln på punkten. Anta att du har en radie på 14 cm och en vinkel på 60.
- I den verkliga världen måste du mäta detta själv, men för dina läxor kommer dessa mått att ges tillsammans med formen.

2. Kvadra radien. Multiplicera radien med sig själv. Detta ger oss ett värde på 196 (14x14).

3. Multiplicera med pi. Pi (π) är ett tal med många decimaler och används i många beräkningar. Om du använder en miniräknare, använd pi-funktionen för ett mycket exakt resultat. Om inte, kan du avrunda pi (ignorera de flesta decimalerna) och bara multiplicera med 3,14159. Detta ger oss ett värde på 615,75164.

4. Dividera vinkeln med 360. Sedan tar du punktens vinkel och dividerar det talet med 360 (antalet grader i en cirkel). I det här fallet får vi ett värde på cirka 0,166. Detta är tekniskt sett ett återkommande nummer, men vi ska avrunda det för att göra matematiken lite lättare.

5. Multiplicera det resulterande talet med talet du beräknade tidigare. Multiplicera talet du får när du dividerar med 360 med talet du beräknade tidigare efter att ha multiplicerat med pi. I det här fallet är resultatet cirka 102 214.

6. Beräkna resultatet. Det slutliga numret är arean av ditt segment, vilket ger segment på 102,214 cm.
Metod 5 av 7: Ellipser

1. Bestäm måtten. För att hitta arean av en ellips behöver du känna till de två "strålarna", som du kan tänka dig som bredd och höjd, var och en dividerad med. Dessa är måtten från mitten till mitten av långsidan och från mitten till mitten av den kortaste sidan. Mätlinjerna skär varandra i räta vinklar.
- I den verkliga världen måste du mäta detta själv, men för dina läxor kommer dessa mått att ges tillsammans med formen.

2. Multiplicera de två strålarna. Anta att ellipsen är 6 cm bred och 4 cm hög. Detta ger oss radier på 3 cm och 2 cm. Nu multiplicerar vi dessa siffror tillsammans, och vi får produkten 6 (3x2).

3. Multiplicera detta tal med pi. Pi (π) är ett exceptionellt långt tal och används i många beräkningar. Om du använder en miniräknare, använd pi-funktionen för ett mycket exakt resultat. Om inte, kan du avrunda pi (ignorera de flesta decimalerna) och bara multiplicera med 3,14159. Detta ger oss ett värde på 18,84954.

4. Bestäm resultatet. Det resulterande talet är arean av din ellips. I det här fallet betyder det att vår ellips är 18,84954 cm.
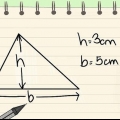
Metod 6 av 7: Triangel

1. Bestäm dina mått. Du måste känna till måtten på triangelns bas, såväl som höjden. Basen kan vara vilken sida som helst av triangeln, så länge du kan mäta höjden. Anta att vi har en triangel med en bas på 3 meter och en höjd på 1 meter.
- I den verkliga världen måste du mäta detta själv, men för dina läxor kommer dessa mått att ges tillsammans med formen.

2. Multiplicera basen med höjden. I det här fallet får vi värdet 3 (3x1).

3. Multiplicera det värdet med 1/2. Detta ger oss ett värde på 1,5.

4. Bestäm resultatet. Det resulterande värdet är arean av triangeln. Så vi får ett resultat på 1,5 m.
Metod 7 av 7: Komplexa former

1. Dela formen i sektioner. Du börjar med att bestämma arean för komplexa former genom att bryta formen i geometriska former, som visas ovan. I hemuppgifter kommer det att vara tydligt vilka former de kommer att vara, men i den verkliga världen måste du dela upp ett plan i många olika former för att få ett korrekt resultat.
- Ett bra ställe att börja är att leta efter räta vinklar och parallella linjer. Dessa utgör grunden för många former.

2. Beräkna arean av de individuella formerna. Använd instruktionerna ovan för att bestämma arean för de olika formerna.

3. Lägg ihop formerna. Lägg samman de resulterande områdena för att hitta den totala ytan av din form.

4. Använd alternativa metoder. Det finns andra knep du också kan prova beroende på formen. Du kan också valfritt lägga till ett imaginärt utrymme för att göra formen till en standardgeometrisk form, och sedan subtrahera arean av det imaginära utrymmet efter att ha bestämt resultatet.
Tips
- Använd denna kalkylator om du behöver mer hjälp och vill veta hur matematiken fungerar.
- Om du tycker att detta är svårt, be någon om hjälp!
Varningar
- Håll enheterna för dina avläsningar desamma. Det är inte meningen att siffror ska blandas ihop!
- Det är alltid en bra idé att dubbelkolla ditt svar!
"Bestämma arean av en form"
Оцените, пожалуйста статью