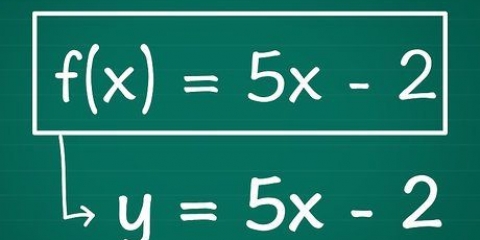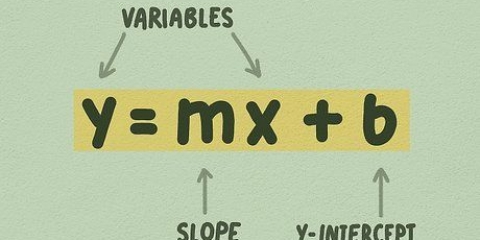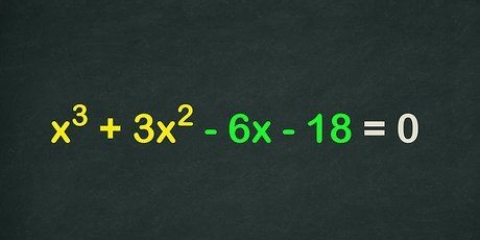Till exempel: standardfunktionen f(x) = 2x +16x + 39. Här har vi a = 2, b = 16 och c = 39. I vertexnotation: f(x) = 4(x - 5) + 12. Här har vi a = 4, h = 5 och k = 12. 
Exempel 1. (f(x) = 2x +16x + 39), h = -b/2a = -16/2(2). När vi löser detta ser vi att h = -4. Exempel 2. (f(x) = 4(x - 5) + 12), vi ser direkt att h = 5. 
Vi har till exempel sett 1 att h = -4. För att nu hitta k löser vi denna ekvation genom att infoga detta värde på h i ekvationen, för variabeln x: k = 2(-4) + 16(-4) + 39. k = 2(16) - 64 + 39. k = 32 - 64 + 39 = 7 Från exempel 2 vet vi att värdet på k är lika med 12, utan att behöva göra en beräkning. 
I exempel 1 är toppen av grafen (-4,7). Rita punkten på din graf och se till att du namnger koordinaterna korrekt. I exempel 2 är toppen (5,12). Så från punkten (0,0) går du 5 platser till höger och sedan 12 upp. 
I fallet med exempel 1 är symmetriaxeln den linje som är parallell med y-axeln och som går genom punkten (-4, 7). Även om det inte är en del av själva parabeln, kan en lätt framhävning av denna riktlinje visa dig hur symmetrisk kurvan för parabeln är. 
I exempel 1 har vi att göra med funktionen (f(x) = 2x +16x + 39), och detta är därför en dalparabel, eftersom a = 2 (positiv). I exempel 2 har vi att göra med funktionen f(x) = 4(x - 5) + 12), och detta är också en dalparabel eftersom a = 4 (positiv). 
Bestäm att f(x) = 0 och lös ekvationen. Denna metod kan fungera för enkla andragradsekvationer, särskilt i vertexformen, men du kommer att upptäcka att det blir svårare och svårare när funktionerna blir mer komplexa. Nedan följer några exempel. f(x) = 4(x - 12) 0 = 4(x - 12) - 4 4 = 4(x - 12) 1 = (x - 12) SqRt(1) = (x - 12) +/- 1 = x -12. x = 11 och 13 är skärningspunkterna med parabelns x-axel. Faktorera ekvationen. Vissa ekvationer av formen ax + bx + c kan enkelt skrivas om som (dx + e)(fx +g), där dx × fx = ax, (dx × g + fx × e) = bx och e × g = c. I det här fallet är x-snitten värdena på x där varje term inom parentesen blir 0. Till exempel: x + 2x + 1 = (x + 1)(x + 1) I det här fallet är skärningspunkten lika med -1 eftersom det, när det fylls i med båda faktorerna, ger noll. Använd abc-formeln. Om det inte är lätt att räkna ut skärningspunkterna, eller faktorisera ekvationen, använd "abc formel" som är speciellt avsedd för detta. Antag en ekvation på formen ax + bx + c. Ange sedan värdena för a, b och c i formeln x = (-b +/- SqRt(b - 4ac))/2a. Observera att detta ofta ger dig två svar för x, vilket är bra - det betyder bara att din parabel har två skärningar med x-axeln. Här är ett exempel: -Infoga 5x + 1x + 10 i ekvationen enligt följande: x = (-1 +/- SqRt(1 - 4(-5)(10)))/2(-5) x = (-1 +/- SqRt(1 + 200))/-10 x = (-1 +/- SqRt(201))/-10 x = (-1 +/- 14,18)/-10 x = (13,18/-10) och (-15,18/-10). Skärningspunkterna mellan parabeln och x-axeln är ungefär x = -1 318 och 1 518 Som i exempel 1 med ekvationen 2x + 16x + 39 kommer detta att se ut så här: x = (-16 +/- SqRt(16 - 4(2)(39))))/2(2) x = (-16 +/- SqRt(256 - 312))/4 x = (-16 +/- SqRt(-56)/-10 Eftersom det inte är möjligt att hitta kvadratroten ur ett negativt tal, vet vi att det inte finns några skärningar med x-axeln för just denna parabel. 
Till exempel vet vi att vår andragradsekvation 2x + 16x + 39 har en skärningspunkt y = 39, men vi kan också hitta detta enligt följande: f(x) = 2x + 16x + 39 f(x) = 2(0) + 16(0) + 39 f(x) = 39. Skärningen av parabeln med y-axeln: y = 39. Som indikerat ovan kan vi enkelt läsa skärningspunkten eftersom y = c. Ekvationen 4(x - 5) + 12 har en skärning med y-axeln som kan hittas enligt följande: f(x) = 4(x - 5) + 12 f(x) = 4(0 - 5) + 12 f(x) = 4(-5) + 12 f(x) = 4(25) + 12 f(x) = 112. Skärningen med y-axeln: y = 112. 
Låt oss ta en ny titt på ekvationen x + 2x + 1. Vi vet redan att den enda skärningspunkten med x-axeln är (-1,0). Eftersom den bara tangerar x-axeln vid denna punkt kan vi dra slutsatsen att grafens spets är lika med denna punkt. Än så länge har vi bara en punkt i denna parabel – inte alls tillräckligt för att kunna rita en graf. Låt oss hitta några fler punkter för att se till att vi har fler värderingar. Låt oss försöka hitta y-värdena som är associerade med följande x-värden: 0, 1, -2 och -3. x=0: f(x) = (0) + 2(0) + 1 = 1. Då är poängen (0,1). x=1: f(x) = (1) + 2(1) + 1 = 4. Då är poängen (1,4). x=-2: f(x) = (-2) + 2(-2) + 1 = 1. Då är poängen (-2,1). x=-3: f(x) = (-3) + 2(-3) + 1 = 4. Då är poängen (-3,4). Placera dessa punkter i grafen och rita din parabel. Observera att parabeln är helt symmetrisk - om du känner till punkterna på ena sidan av grafen kan du vanligtvis spara mycket arbete genom att använda dessa punkter för att hitta punkterna på andra sidan av symmetriaxeln.
Plotta en funktion
Som en graf ser en andragradsekvation axe + bx + c, även någon skriven soma(x - h) + k, ser ut som en slät kurva i en U-form. Detta är vad vi kallar a parabel. Att rita en andragradsekvation innebär att man hittar vertex, riktning och ofta skärningspunkter med x-axeln och y-axeln. När det gäller den relativt enkla andragradsekvationen kan det också räcka att ange ett antal värden för x för att indikera dessa punkter i koordinatsystemet, varefter parabeln kan ritas. Fortsätt till steg 1 för att komma igång.
Steg

1. Bestäm vilken typ av andragradsekvation du har. Detta kan skrivas på två sätt: standardnotationen och vertexnotationen (ett annat sätt att skriva kvadratrotsformeln). Du kan använda båda för att göra en graf av en andragradsekvation, men denna process är något annorlunda i båda fallen. Vanligtvis kommer du att stöta på standardformuläret, men det skadar verkligen inte att lära dig använda båda formerna. De två formerna av en andragradsekvation är: Spetsformen. Här skrivs andragradsekvationen som: f(x) = a(x - h) + k där a, h och k är reella tal och a inte är lika med noll. Denna form kallas vertex eftersom h och k hänvisar direkt till vertex på din parabel vid punkten (h,k). Två exempel på ekvationer i vertexform är f(x) = 9(x - 4) + 18 och -3(x - 5) + 1 För att kunna göra en graf av dessa ekvationer bestämmer vi först toppen (h,k) på grafen. I standardekvationen kan du hitta detta via: h = -b/2a och k = f(h), medan det redan ges i vertexform eftersom h och k förekommer i ekvationen.
- Standardformen. Här skrivs andragradsekvationen som: f(x) = ax + bx + c där a, b och c är reella tal och a inte är lika med noll.
- Två exempel på vanliga andragradsekvationer: f(x) = x + 2x + 1 och f(x) = 9x + 10x -8.

2. Bestäm dina variabler. För att lösa en andragradsekvation är det vanligtvis nödvändigt att bestämma variablerna a, b och c (eller a, h och k). Ett vanligt problem kommer att ge dig en andragradsekvation i standardformen, men vertexnotationen kan också förekomma.

3. Beräkna h. I vertexnotationen är värdet på h redan givet, men i standardnotationen har detta värde ännu inte beräknats. Kom ihåg att för standardekvationen, h = -b/2a.

4. Beräkna k. Liksom med h är k redan känt för ekvationer i vertexformen. För ekvationer i standardnotation, kom ihåg att k = f(h). Med andra ord kan du hitta k genom att ersätta varje variabel x med värdet av h.

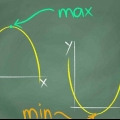
5. Rita toppen eller botten av grafen. Krönet eller dalen av din parabel är punkten (h, k) - h representerar x-koordinaten och k representerar y-koordinaten. Krönet är mitten av din parabel - den högsta eller lägsta punkten, krönet eller dalgången, av en graf i form av en "DU" eller tvärtom. Att kunna bestämma spetsen på en parabel är en viktig del av att kunna rita en korrekt graf – ofta är att fastställa en parabels vertex en del av ett matematiskt problem i skolan.

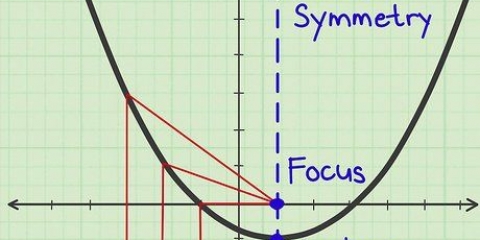
6. Rita symmetriaxeln för parabeln. Symmetriaxeln för en parabel är linjen som skär figuren i mitten och delar den exakt på mitten. Ena sidan av grafen speglas längs denna linje på den andra sidan av grafen. För andragradsekvationer av antingen formen ax + bx + c eller a(x - h) + k, är denna axel linjen parallell med y-axeln som går genom parabelns spets.

7. Bestäm riktningen för parabeln. Efter att du har tagit reda på vad toppen av parabeln är, är det nödvändigt att veta om du har att göra med en bergsparabel eller en dalparabel, d.v.s. om öppningen är längst ner eller överst. Lyckligtvis är detta väldigt enkelt. om "a" positivt att du har att göra med en dalparabel; är "a" negativt då är det en bergsparabel (med öppningen längst ner)

8. Bestäm, om nödvändigt, skärningspunkterna för parabeln. I matematiska problem blir du ofta ombedd att ange skärningspunkterna mellan parabeln och x-axeln (dessa är "noll-", a eller två punkter där parabeln skär eller rör vid x-axeln). Även om de inte efterfrågas är dessa punkter mycket viktiga för att kunna rita en korrekt graf. Men alla paraboler skär inte x-axeln. Om du har att göra med en dalparabel och dalpunkten är ovanför x-axeln eller, i fallet med en bergsparabel, strax under x-axeln, så finns det helt enkelt inga skärningspunkter att hitta. Om så är fallet, använd någon av följande metoder:

9. Bestäm vid behov skärningspunkten för parabeln med y-axeln. Det är ofta inte nödvändigt, men ibland krävs för att hitta denna skärningspunkt, till exempel för ett matematiskt problem. Detta är ganska enkelt - sätt värdet på x till 0 och lös ekvationen för f(x) eller y, vilket ger dig y-värdet för punkten där parabeln skär y-axeln. Skillnaden med skärningspunkterna genom x-axeln är att det med y-axeln alltid bara finns en skärningspunkt. Notera – för standardekvationer är skärningen med y-axeln vid y = c.

10. Om du tycker att det är nödvändigt, rita först extra poäng och sedan hela grafen. Du bör nu ha en topp eller dal, en riktning, skärningar med x-axeln och eventuellt med y-axeln i din ekvation. Från denna punkt kan du försöka rita parabeln med dessa punkter eller så kan du försöka hitta fler punkter för att göra grafen mer exakt. Det enklaste sättet att göra detta är att helt enkelt fylla i ett antal x-värden, vilket returnerar ett antal y-värden. Du kommer ofta att bli ombedd (av läraren) att först räkna ut ett antal poäng innan du kan rita parabeln.
Tips
- Runda siffror vid behov eller använd bråk. Detta kan hjälpa till att visa en graf korrekt.
- Observera att om, för funktionen f(x) = ax + bx + c, b eller c är lika med noll, kommer dessa termer att försvinna. Till exempel, 12x + 0x + 6 är lika med 12x + 6 eftersom 0x är lika med 0.
Оцените, пожалуйста статью