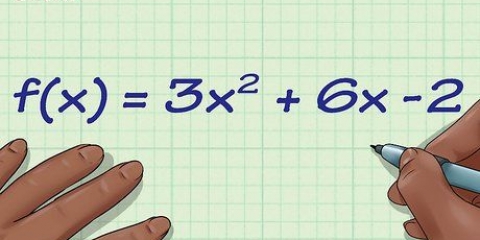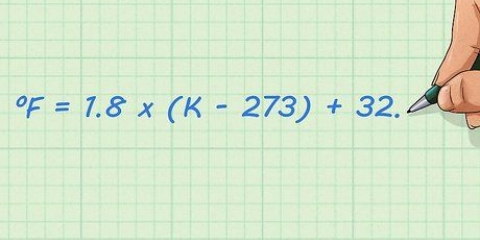blir
blir 
 blir
blir 
 blir
blir  .
.








Om de två resultaten är samma, då är f(x)=f(-x), och den ursprungliga funktionen är jämn. Ett exempel är:  och
och  .
.Dessa två är desamma och funktionen är därför jämn. Om varje term i den nya versionen av funktionen är den reciproka till motsvarande term i originalet, då är f(x)=-f(-x) och funktionen är udda. Till exempel:  men
men  .
.Observera att om du multiplicerar varje led i den första funktionen med -1, gör du den andra funktionen. Så den ursprungliga funktionen g(x) är udda. Om den nya funktionen inte matchar något av dessa två exempel är den varken jämn eller udda. Till exempel:  men
men  . Den första termen är densamma i alla funktioner, men den andra termen är en invers. Därför är denna funktion varken jämn eller udda.
. Den första termen är densamma i alla funktioner, men den andra termen är en invers. Därför är denna funktion varken jämn eller udda.

Du kan testa symmetri genom att välja enskilda punkter. Om y-värdet för ett x-värde är detsamma som y-värdet för -x, så är funktionen jämn. Punkterna som valts ovan för plottning  ge följande resultat:
ge följande resultat: (1,3) och (-1,3) (2,9) och (-2,9). Motsvarande y-värden för x=1 och x=-1, och för x=2 och x=-2, indikerar att detta är en jämn funktion. För ett bättre test är att välja två punkter inte tillräckligt med bevis, men det är en bra indikation. 
Om du väljer ett par testvärden för x och deras inversa motsvarande värden för -x, bör du få omvända resultat. Tänk på funktionen  . Denna funktion returnerar följande punkter:
. Denna funktion returnerar följande punkter:  . Poängen är (1,2).
. Poängen är (1,2). . Poängen är (-1,-2).
. Poängen är (-1,-2). . Poängen är (2,10).
. Poängen är (2,10). . Poängen är (-2,-10).
. Poängen är (-2,-10).Alltså f(x)=-f(-x), och du kan dra slutsatsen att funktionen är udda. 
Välj ett värdepar för x och -x, enligt följande:  . Poängen att plotta är (1,4).
. Poängen att plotta är (1,4). . Poängen att plotta är (-1,-2).
. Poängen att plotta är (-1,-2). . Poängen att plotta är (2,10).
. Poängen att plotta är (2,10). . Poängen att plotta är (2,-2).
. Poängen att plotta är (2,-2).Detta ger dig redan tillräckligt många poäng för att märka att det inte finns någon symmetri. Y-värdena för motsatta par av x-värden är inte desamma, och de är inte heller varandras inversa. Denna funktion är varken jämn eller udda. Du kanske ser den här funktionen,  , kan skrivas om som
, kan skrivas om som  . Skrivet i den här formen ser det ut som om det är en jämn funktion eftersom det bara finns en exponent, och det är ett jämnt tal. Det här exemplet illustrerar dock att du inte kan avgöra om en funktion är jämn eller udda när den är omgiven av parentes. Du måste utvärdera funktionen i individuella termer och sedan granska exponenterna.
. Skrivet i den här formen ser det ut som om det är en jämn funktion eftersom det bara finns en exponent, och det är ett jämnt tal. Det här exemplet illustrerar dock att du inte kan avgöra om en funktion är jämn eller udda när den är omgiven av parentes. Du måste utvärdera funktionen i individuella termer och sedan granska exponenterna.
Vet om en funktion är jämn eller udda
Ett sätt att klassificera funktioner är antingen `jämn`, `udda` eller ingetdera. Dessa termer hänvisar till funktionens upprepning eller symmetri. Det bästa sättet att ta reda på det är genom att algebraiskt manipulera funktionen. Du kan också studera grafen för funktionen och leta efter symmetri. När du väl vet hur man klassificerar funktioner kan du också förutsäga utseendet på vissa kombinationer av funktioner.
Steg
Metod 1 av 2: Testa funktionen algebraiskt

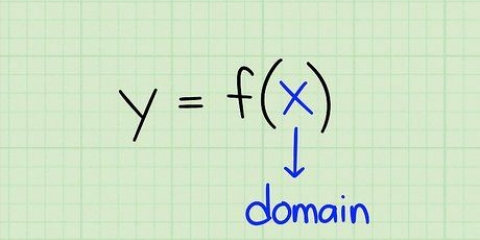
1. Visa inversa variabler. I algebra är den reciproka av en variabel negativ. Detta är sant eller variabeln för funktionen nu  är eller något annat. Om variabeln för den ursprungliga funktionen redan är negativ (eller en subtraktion), är dess reciproka positiv (eller en addition). Följande är några exempel på variabler och deras inverser:
är eller något annat. Om variabeln för den ursprungliga funktionen redan är negativ (eller en subtraktion), är dess reciproka positiv (eller en addition). Följande är några exempel på variabler och deras inverser:
 är eller något annat. Om variabeln för den ursprungliga funktionen redan är negativ (eller en subtraktion), är dess reciproka positiv (eller en addition). Följande är några exempel på variabler och deras inverser:
är eller något annat. Om variabeln för den ursprungliga funktionen redan är negativ (eller en subtraktion), är dess reciproka positiv (eller en addition). Följande är några exempel på variabler och deras inverser: - Det omvända av
är
- Det omvända av
är
- Det omvända av
är
.

2. Ersätt varje variabel i funktionen med dess invers. Ändra inte den ursprungliga funktionen förutom tecknet. Till exempel:
 blir
blir 
 blir
blir 
 blir
blir  .
.
3. Förenkla den nya funktionen. Vid det här laget behöver du inte oroa dig för att lösa funktionen för ett givet numeriskt värde. Du förenklar bara variablerna för att jämföra den nya funktionen, f(-x), med den ursprungliga funktionen, f(x). Kom ihåg de grundläggande reglerna för exponenter som säger att en negativ bas till en jämn potens kommer att vara positiv, medan en negativ bas till en udda potens kommer att vara negativ.








4. Jämför de två funktionerna. För varje exempel du försöker, jämför den förenklade versionen av f(-x) med den ursprungliga f(x). Lägg termerna sida vid sida för enkel jämförelse och jämför tecknen på alla termer.
 och
och  .
. men
men  .
. men
men  . Den första termen är densamma i alla funktioner, men den andra termen är en invers. Därför är denna funktion varken jämn eller udda.
. Den första termen är densamma i alla funktioner, men den andra termen är en invers. Därför är denna funktion varken jämn eller udda.Metod 2 av 2: Testa funktionen grafiskt

1. Plotta funktionen. Använd diagrampapper eller en grafräknare för att rita funktionen. Välj olika numeriska värden för  och koppla in det i funktionen för att få det resulterande värdet av
och koppla in det i funktionen för att få det resulterande värdet av  att räkna ut. Rita dessa punkter på grafen och efter att ha ritat flera punkter dra en linje genom dem för att rita funktionen.
att räkna ut. Rita dessa punkter på grafen och efter att ha ritat flera punkter dra en linje genom dem för att rita funktionen.
 och koppla in det i funktionen för att få det resulterande värdet av
och koppla in det i funktionen för att få det resulterande värdet av  att räkna ut. Rita dessa punkter på grafen och efter att ha ritat flera punkter dra en linje genom dem för att rita funktionen.
att räkna ut. Rita dessa punkter på grafen och efter att ha ritat flera punkter dra en linje genom dem för att rita funktionen. - När du ritar punkterna, var uppmärksam på positiva och motsvarande negativa värden för
. Till exempel om du har att göra med funktionen
, sedan ritar du följande värden:
. Detta resulterar i poängen
.
. Detta resulterar i poängen
.
. Detta resulterar i poängen
.
. Detta resulterar i poängen
.

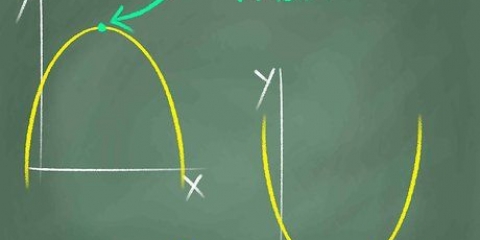
2. Notera symmetri längs y-axeln. När man tittar på en funktion kommer symmetri att föreslå en spegelbild. Om du ser att den del av grafen på den högra (positiva) sidan av y-axeln matchar den del av grafen på den vänstra (negativa) sidan av y-axeln, så är grafen symmetrisk kring y-axeln. Om en funktion är symmetrisk kring y-axeln är funktionen jämn.
 ge följande resultat:
ge följande resultat:
3. Testa för symmetri från ursprunget. Ursprunget är den centrala punkten (0,0). Ursprungssymmetri innebär att ett positivt resultat för ett valt x-värde kommer att motsvara ett negativt resultat för -x, och vice versa. Udda funktioner uppvisar ursprungssymmetri.
 . Denna funktion returnerar följande punkter:
. Denna funktion returnerar följande punkter: . Poängen är (1,2).
. Poängen är (1,2). . Poängen är (-1,-2).
. Poängen är (-1,-2). . Poängen är (2,10).
. Poängen är (2,10). . Poängen är (-2,-10).
. Poängen är (-2,-10).
4. Se om det inte finns någon symmetri. Det sista exemplet är en funktion utan symmetri på båda sidor. Om du tittar på grafen ser du att det inte är en spegelbild varken på y-axeln eller runt origo. Se funktionen  .
.
 .
. . Poängen att plotta är (1,4).
. Poängen att plotta är (1,4). . Poängen att plotta är (-1,-2).
. Poängen att plotta är (-1,-2). . Poängen att plotta är (2,10).
. Poängen att plotta är (2,10). . Poängen att plotta är (2,-2).
. Poängen att plotta är (2,-2). , kan skrivas om som
, kan skrivas om som  . Skrivet i den här formen ser det ut som om det är en jämn funktion eftersom det bara finns en exponent, och det är ett jämnt tal. Det här exemplet illustrerar dock att du inte kan avgöra om en funktion är jämn eller udda när den är omgiven av parentes. Du måste utvärdera funktionen i individuella termer och sedan granska exponenterna.
. Skrivet i den här formen ser det ut som om det är en jämn funktion eftersom det bara finns en exponent, och det är ett jämnt tal. Det här exemplet illustrerar dock att du inte kan avgöra om en funktion är jämn eller udda när den är omgiven av parentes. Du måste utvärdera funktionen i individuella termer och sedan granska exponenterna.Tips
- Om alla former av en variabel i funktionen har jämna exponenter, så är funktionen jämn. Om alla exponenter är udda, är funktionen totalt sett udda.
Varning
- Denna artikel gäller endast funktioner med två variabler, som kan ritas i ett tvådimensionellt koordinatsystem.
"Vet om en funktion är jämn eller udda"
Оцените, пожалуйста статью