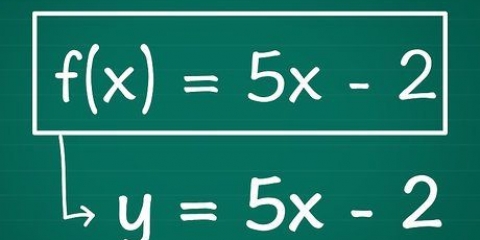Bearbeta sedan -1 i funktionen för att få y-koordinaten. f(-1) = 3(-1) + 6(-1) -2 = 3 - 6 -2 = -5. Spetsen på parabeln är (-1,-5). Bearbeta detta i grafen genom att rita en punkt vid x-koordinat -1 och y-koordinat -5. Detta bör vara i den tredje kvadranten av grafen. 
f(-2) = 3(-2) + 6(-2) -2 = -2. En punkt på grafen är (-2, -2) f(0) = 3(0) + 6(0) -2 = -2. En annan punkt på grafen är (0,-2) f(1) = 3(1) + 6(1) -2 = 7. En tredje punkt på grafen är (1, 7). 



Men anta att y = -3 är den lägsta punkten i grafen, men stiger för alltid. Då är området f(x) ≥ -3, och inte mer än så. Antag att grafen når sin högsta punkt vid y=10, men fortsätter sedan att falla för alltid. Då är området f(x) ≤ 10. 






Till exempel: Om hon säljer 2 lotter måste du multiplicera 2 med 5, med 10 som svar, och därmed det totala insamlade beloppet. 

Det vill säga ett positivt heltal som är en multipel av fem är ett möjligt resultat av funktionen.
Bestämma omfattningen av en funktion
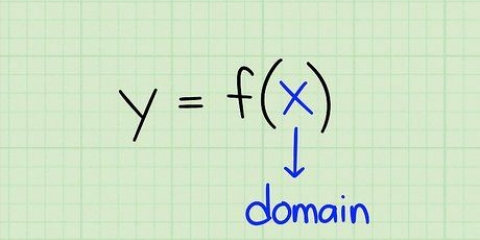
Omfånget för en funktion är den uppsättning tal som funktionen kan producera. Det är med andra ord mängden y-värden du får när du räknar in alla möjliga x-värden i funktionen. Denna uppsättning av x-värden kallas domänen. Om du vill veta hur man beräknar omfånget för en funktion, följ stegen nedan.
Steg
Metod 1 av 4: Bestämma intervallet för en funktion med en given ekvation

1. Skriv ner ekvationen. Anta att du har följande ekvation: f(x) = 3x + 6x -2. Detta betyder att när du anger ett värde för X av ekvationen, att du då har en y-får värde. Detta är funktionen av en parabel.

2. Hitta toppen av funktionen, om det är en andragradsekvation. Om du har en rät linje eller någon funktion med ett polynom eller ett udda tal, till exempel f(x) = 6x+2x + 7, kan du hoppa över detta steg. Men om du har att göra med en parabel eller en ekvation där x-koordinaten är kvadratisk eller ökad med en jämn potens, måste du rita spetsen på parabeln. För att göra detta, använd ekvationen -b/2a för x-koordinaten för funktionen 3x + 6x -2, där 3 = a, 6 = b och -2 = c. I detta fall, -b är -6 och 2a är 6, så x-koordinaten är -6/6 eller -1.

3. Hitta några andra punkter i funktionen. För att få en känsla för funktionen bör du fylla i några andra värden för x så att du kan få en uppfattning om hur funktionen ser ut innan du börjar leta efter intervallet. Eftersom det är en parabel och x är positivt kommer parabeln att peka uppåt (dalparabel). Men bara för att vara säker anger vi några fler värden för x för att se vilka y-koordinater de ger:

4. Hitta intervallet för diagrammet. Titta nu på y-koordinaterna på grafen och hitta den lägsta punkten där grafen vidrör y-koordinaten. I detta fall är den lägsta y-koordinaten överst på parabeln, -5 och grafen sträcker sig oändligt bortom denna punkt. Detta innebär att räckvidden för funktionen y = alla reella tal ≥ -5.
Metod 2 av 4: Bestämma intervallet för en funktion med hjälp av en graf

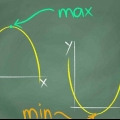
1. Hitta minimum av funktionen. Hitta den lägsta y-koordinaten för funktionen. Antag att funktionen når sin lägsta punkt vid -3. Denna funktion kan bli mindre och mindre, till oändlighet, så den har ingen fast lägsta punkt - bara oändligt.

2. Hitta det maximala av funktionen. Antag att den högsta y-koordinaten för funktionen är 10. Denna funktion kan också bli oändligt mycket större, så den har ingen fast högsta punkt – bara oändlig.

3. Ange vad intervallet är. Detta betyder att intervallet för funktionen, eller intervallet för y-koordinaterna, är från -3 till 10. Alltså -3 ≤ f(x) ≤ 10. Det är funktionens omfattning.
Metod 3 av 4: Bestämma omfattningen av en relations funktion

1. Skriv ner förhållandet. En relation är en uppsättning ordnade par av x- och y-koordinater. Du kan titta på ett förhållande och bestämma dess domän och omfattning. Anta att du har att göra med följande relation: {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)}.

2. Lista y-koordinaterna för förhållandet. För att bestämma intervallet för sambandet skriver vi ner alla y-koordinater för varje ordnat par: {-3, 6, -1, 6, 3}.

3. Ta bort alla dubbletter av koordinater så att du bara har en av varje y-koordinat. Du kanske har märkt att du har "6" två gånger i listan. Ta bort det så att du har {-3, -1, 6, 3}.

4. Skriv intervallet för relationen i stigande ordning. Ordna sedan siffrorna i uppsättningen från minsta till största, och du har hittat intervallet. Intervallet för relationen {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)} är {-3,-1, 3, 6}. Du är klar.

5. Gör relationen till en funktion är. För att en relation ska vara en funktion, varje gång du anger ett tal från en x-koordinat måste y-koordinaten vara densamma. Till exempel är relationen {(2, 3) (2, 4) (6, 9)} Nej funktion, för om du fyller i 2:an som x för första gången får du en 3:a som värde, men andra gången du fyller i en 2:a får du fyra. En relation är bara en funktion om man alltid får samma utdata för en viss ingång. Om du anger -7 ska du alltid få samma y-koordinat (vad det än kan vara), varje gång.
Metod 4 av 4: Bestäm omfattningen av en funktion i ett problem

1. Läs frågan. Anta att du arbetar med följande problem: "Becky säljer biljetter till sin skolas talangshow för $5 styck. Det totala beloppet hon samlar in är en funktion av antalet biljetter hon säljer. Vad är räckvidden för funktionen?"

2. Skriv problemet som en funktion. I detta fall m det belopp som har samlats in och t antalet sålda biljetter. Eftersom varje biljett kostar 5 euro måste du multiplicera antalet sålda biljetter med 5 för att få det totala beloppet. Därför kan funktionen skrivas som M(t) = 5t.

3. Bestäm vad domänen är. För att hitta sortimentet behöver du först domänen. Domänen består av alla möjliga värden på t som deltar i ekvationen. I det här fallet kan Becky sälja 0 eller fler biljetter – hon kan inte sälja ett negativt antal biljetter. Eftersom vi inte vet antalet platser i skolans aula kan vi anta att hon i teorin kan sälja oändligt många biljetter. Och hon kan bara sälja hela biljetter, inte en del av dem. Därför domänen för funktionen t = något positivt heltal.

4. Bestäm vad intervallet är. Intervallet är det möjliga beloppet som Becky kan samla in med försäljningen. Du måste arbeta med domänen för att hitta sortimentet. Om du vet att domänen består av ett positivt heltal och att ekvationen M(t) = 5t då vet du också att du kan ange vilket positivt heltal som helst i denna funktion för svaret, eller området. Till exempel: Om hon säljer 5 biljetter så är M(5) = 5 x 5, eller 25 euro. Om hon säljer 100 så är M(100) = 5 x 100, eller 500 euro. Därför räckvidden för funktionen vilket positivt heltal som helst som är en multipel av fem.
Tips
- Se om du kan hitta inversen av funktionen. Domänen för inversen av en funktion är lika med intervallet för den funktionen.
- I de svårare fallen kan det vara lättare att först plotta grafen med hjälp av domänen (om nödvändigt) och sedan läsa av intervallet från grafen.
- Kontrollera om funktionen upprepas. Alla funktioner som upprepas längs x-axeln kommer att ha samma intervall för hela funktionen. Till exempel: f(x) = sin(x) har ett intervall mellan -1 och 1.
"Bestämma omfattningen av en funktion"
Оцените, пожалуйста статью