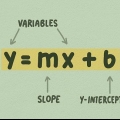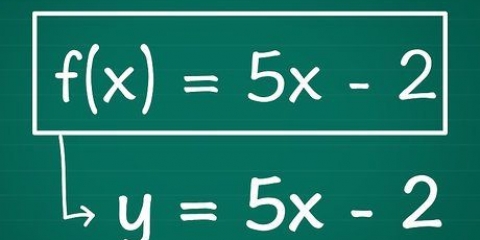Om lutningen är negativ betyder det att linjen går ner när du går till höger. 





-1: -1 + 2 = 1 0: 0 +2 = 2 1: 1 + 2 = 3 




Gör F(x) lika med noll:
Lösa:




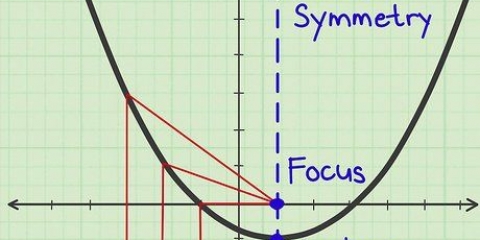
Vissa kvadratiska funktioner, som t.ex  är aldrig negativa. Så det finns en asymptot vid 0.
är aldrig negativa. Så det finns en asymptot vid 0. Om du inte arbetar med imaginära siffror är detta inte möjligt: 
Ekvationer med komplexa exponenter kan ha många asymptoter. 
För jämförelsen  , kan du fylla i -1, 0, 1, -2, 2, -10 och 10. Detta ger dig ett bra utbud av siffror att jämföra.
, kan du fylla i -1, 0, 1, -2, 2, -10 och 10. Detta ger dig ett bra utbud av siffror att jämföra. Var smart med att välja siffror. I exemplet märker du snabbt att ett negativt tecken inte spelar någon roll - du kan till exempel sluta testa -10, eftersom det blir samma som 10. 
Antag två till fyra stora värden för x, hälften negativt och hälften positivt, och rita prickarna. Vad händer om du infogar `oändlighet` för en variabel? Blir funktionen oändligt mycket större eller mindre? Om graderna är lika i en bråkdel, som t.ex  , dividera sedan de två första koefficienterna (
, dividera sedan de två första koefficienterna ( för att få din sista asymptot (-0,5).
för att få din sista asymptot (-0,5). Om graderna i ett bråk är olika, dividera ekvationen i täljaren med ekvationen i nämnaren med långdivision av polynom. 

Rita grafen för en funktion
En graf över en funktion är en visuell representation av beteendet hos en funktion på ett x-y-plan. Grafer hjälper oss att förstå olika aspekter av funktionen som skulle vara svåra att förstå bara genom att titta på själva funktionen. Du kan rita tusentals ekvationer, och det finns olika formler för varje ekvation. Det finns dock alltid sätt att plotta en funktion om du glömt de exakta stegen för den specifika typen av funktion.
Steg
Metod 1 av 3: Rita en linjär ekvation med en tangent

1. Vet att linjära funktioner är enkla linjer som är lätta att rita, som t.ex y = 2 X + 5  . Det finns en variabel och en konstant, skrivna som
. Det finns en variabel och en konstant, skrivna som  i en linjär funktion, utan exponenter, radikaler osv. Om du har en så enkel ekvation är grafen för funktionen också enkel. Andra exempel på linjära funktioner är:
i en linjär funktion, utan exponenter, radikaler osv. Om du har en så enkel ekvation är grafen för funktionen också enkel. Andra exempel på linjära funktioner är:
 . Det finns en variabel och en konstant, skrivna som
. Det finns en variabel och en konstant, skrivna som  i en linjär funktion, utan exponenter, radikaler osv. Om du har en så enkel ekvation är grafen för funktionen också enkel. Andra exempel på linjära funktioner är:
i en linjär funktion, utan exponenter, radikaler osv. Om du har en så enkel ekvation är grafen för funktionen också enkel. Andra exempel på linjära funktioner är: 
2. Använd konstanten för att indikera skärningspunkten med y-axeln. Skärningen med y-axeln är den punkt där funktionen korsar y-axeln på din graf. Det är med andra ord punkten där  . Så för att hitta det, sätt bara x till noll och lämna konstanten i ekvationen. I föregående exempel,
. Så för att hitta det, sätt bara x till noll och lämna konstanten i ekvationen. I föregående exempel,  , är skärningspunkten med y-axeln lika med y=5, dvs punkten (0,5). Markera denna plats på ditt diagram med en prick.
, är skärningspunkten med y-axeln lika med y=5, dvs punkten (0,5). Markera denna plats på ditt diagram med en prick.
 . Så för att hitta det, sätt bara x till noll och lämna konstanten i ekvationen. I föregående exempel,
. Så för att hitta det, sätt bara x till noll och lämna konstanten i ekvationen. I föregående exempel,  , är skärningspunkten med y-axeln lika med y=5, dvs punkten (0,5). Markera denna plats på ditt diagram med en prick.
, är skärningspunkten med y-axeln lika med y=5, dvs punkten (0,5). Markera denna plats på ditt diagram med en prick.
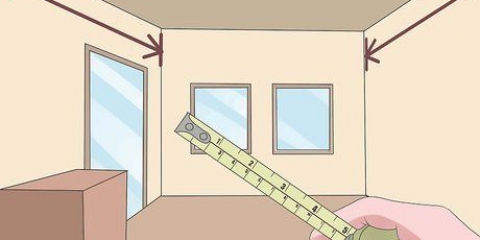
3. Hitta lutningen på din linje med talet precis före variabeln. I exemplet,  , är lutningen `2`. Det beror på att 2 tillhör variabeln `x`. Lutningen anger hur brant en linje är, eller hur hög linjen går innan den svänger till höger eller vänster. En större lutning innebär en brantare linje.
, är lutningen `2`. Det beror på att 2 tillhör variabeln `x`. Lutningen anger hur brant en linje är, eller hur hög linjen går innan den svänger till höger eller vänster. En större lutning innebär en brantare linje.
 , är lutningen `2`. Det beror på att 2 tillhör variabeln `x`. Lutningen anger hur brant en linje är, eller hur hög linjen går innan den svänger till höger eller vänster. En större lutning innebär en brantare linje.
, är lutningen `2`. Det beror på att 2 tillhör variabeln `x`. Lutningen anger hur brant en linje är, eller hur hög linjen går innan den svänger till höger eller vänster. En större lutning innebär en brantare linje.
4. Gör en bråkdel av lutningen. Lutningen har att göra med brantheten, och brantheten är helt enkelt skillnaden mellan rörelsen upp och ner, och vänster och höger. Lutningen är en bråkdel av förändringen av y jämfört med förändringen av x. Hur mycket måste raden "byta över y" innan den "byta över x"? I exemplet kan lutningen `2` läsas som  .
.
 .
.
5. Börja vid din skärningspunkt med y-axeln och följ ändringarna över y och x, för att rita fler punkter. När du känner till lutningen, använd den för att rita din linjära funktion. Börja vid korsningen med y-axeln, här (0,5), gå sedan upp 2 och höger 1. Markera även denna punkt (1,7). Hitta ytterligare 1-2 punkter för att rita grafen.

6. Använd en linjal för att koppla ihop dina punkter och rita din linjära funktion. För att undvika misstag eller grova grafer, hitta och anslut minst tre separata punkter, även om två räcker i en nödsituation. Detta är grafen för din linjära ekvation!
Metod 2 av 3: Beräkna poäng på en graf

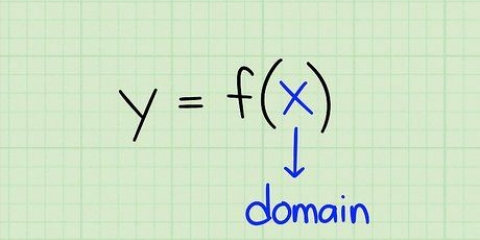
1. Bestäm funktionen. Ta formulärets funktion f(X), Sann y representerar intervallet, X representerar domänen och f funktionen. Som exempel använder vi y = x+2, varigenom f(X) = x+2.

2. Rita två korsade linjer på ett pappersark. Den horisontella linjen är du X-aska. Den vertikala linjen är du y-aska.

3. Numrera ditt diagram. Markera både X-som om y-axel med siffror på samma avstånd från varandra. För X-axel är talen positiva till höger och negativa till vänster. För y-axel är siffrorna positiva upptill och negativa längst ned.

4. Beräkna a y-värde för 2-3 X-värden. Anta funktionen f(X) = x+2. Beräkna några värden för y med motsvarande värden för X synlig på axeln i funktionen. För mer komplicerade ekvationer kan det vara nödvändigt att förenkla funktionen genom att först isolera en variabel.

5. Rita grafpunkten för varje par. Rita imaginära tunna vertikala linjer längs med X-axeln och horisontellt längs y-aska. Punkten där dessa linjer skär varandra är en grafpunkt (eller använd bara millimeterpapper).

6. Ta bort de imaginära linjerna. När du har ritat alla grafpunkter kan du radera de tänkta linjerna. Notera: grafen för f(x) = x skulle vara en linje parallell med den genom origo (0,0), men f(x) = x+2 är förskjuten två enheter (längs y-axeln) på rutnätet på grund av +2 i ekvationen.
Metod 3 av 3: Plotta en komplex funktion

1. Förstå hur man grafiskt representerar vanliga typer av ekvationer. Det finns lika många olika kartläggningsstrategier som det finns typer av funktioner, alldeles för många för att helt täcka här. Om du tycker att detta är svårt och en uppskattning inte fungerar, kolla in artiklar om:
- Kvadratiska funktioner
- Rationella funktioner
- Logaritmiska funktioner
- Ojämlikheter (inga funktioner, men användbar information ändå).

2.Bestäm först nollorna. Nollor är de punkter där grafen skär den horisontella linjen på grafen. Även om inte alla grafer har nollor, har de flesta det, och det är det första steget du måste ta för att få allt rätt. För att hitta nollor, ställ först hela funktionen till noll och lös den sedan. Till exempel:







3. Hitta och markera eventuella horisontella asymptoter (platser där funktionen är omöjlig att nå) med en prickad linje. Det är vanligtvis punkter där grafen inte finns, till exempel där du dividerar med noll. Om din ekvation har en variabel i ett bråk, som t.ex  , börja sedan med att nollställa botten av bråket. Du kan kartlägga alla platser där det är lika med noll (i detta exempel en prickad linje vid x=2 och x=-2), eftersom du aldrig kan dividera med noll. Men bråk är inte de enda platserna att hitta asymptoter. Vanligtvis allt du behöver är lite sunt förnuft:
, börja sedan med att nollställa botten av bråket. Du kan kartlägga alla platser där det är lika med noll (i detta exempel en prickad linje vid x=2 och x=-2), eftersom du aldrig kan dividera med noll. Men bråk är inte de enda platserna att hitta asymptoter. Vanligtvis allt du behöver är lite sunt förnuft:
 , börja sedan med att nollställa botten av bråket. Du kan kartlägga alla platser där det är lika med noll (i detta exempel en prickad linje vid x=2 och x=-2), eftersom du aldrig kan dividera med noll. Men bråk är inte de enda platserna att hitta asymptoter. Vanligtvis allt du behöver är lite sunt förnuft:
, börja sedan med att nollställa botten av bråket. Du kan kartlägga alla platser där det är lika med noll (i detta exempel en prickad linje vid x=2 och x=-2), eftersom du aldrig kan dividera med noll. Men bråk är inte de enda platserna att hitta asymptoter. Vanligtvis allt du behöver är lite sunt förnuft: är aldrig negativa. Så det finns en asymptot vid 0.
är aldrig negativa. Så det finns en asymptot vid 0.

4. Tillämpa värdena och rita olika punkter. Välj bara några värden för x och lös för funktionen. Gör sedan en graf över punkterna på din graf. Ju mer komplicerad grafen är, desto fler poäng behöver du. I allmänhet är -1, 0 och 1 de enklaste poängen att få, även om du vill ha två eller tre till på vardera sidan av nollan för att få en bra graf.
 , kan du fylla i -1, 0, 1, -2, 2, -10 och 10. Detta ger dig ett bra utbud av siffror att jämföra.
, kan du fylla i -1, 0, 1, -2, 2, -10 och 10. Detta ger dig ett bra utbud av siffror att jämföra.
5. Kartlägg funktionens slutbeteende för att se vad som händer när den blir riktigt stor. Detta ger dig en uppfattning om den allmänna riktningen för en funktion, vanligtvis som en vertikal asymptot. Till exempel: det vet du  blir så småningom väldigt, väldigt stor. Bara ett extra "x" (en miljon mot en miljon och en) gör y mycket större. Det finns några sätt att testa slutbeteendet, inklusive:
blir så småningom väldigt, väldigt stor. Bara ett extra "x" (en miljon mot en miljon och en) gör y mycket större. Det finns några sätt att testa slutbeteendet, inklusive:
 blir så småningom väldigt, väldigt stor. Bara ett extra "x" (en miljon mot en miljon och en) gör y mycket större. Det finns några sätt att testa slutbeteendet, inklusive:
blir så småningom väldigt, väldigt stor. Bara ett extra "x" (en miljon mot en miljon och en) gör y mycket större. Det finns några sätt att testa slutbeteendet, inklusive: , dividera sedan de två första koefficienterna (
, dividera sedan de två första koefficienterna ( för att få din sista asymptot (-0,5).
för att få din sista asymptot (-0,5).
6. Anslut prickarna, undvik asymptotiskt beteende och slutbeteende, för att uppskatta grafen. När du har fem eller sex punkter, asymptoterna och en allmän uppfattning om slutbeteendet, använd alla dessa för att konstruera en ungefärlig version av grafen.

7. Ge perfekta grafer med hjälp av en grafräknare. Grafräknare är kraftfulla handdatorer som kan ge exakta grafer för alla ekvationer. De låter dig lokalisera exakta punkter, hitta lutningslinjer och visualisera svåra ekvationer med lätthet. Ange bara den exakta ekvationen i grafsektionen (vanligtvis en knapp märkt `F(x) = `) och tryck på grafknappen för att få en uppfattning om funktionen.
Tips
- Grafräknare är ett bra sätt att öva på. Försök att göra en graf för hand och använd sedan kalkylatorn för att få en perfekt bild av grafen, jämför sedan båda graferna.
- Om du verkligen inte vet vad du ska göra längre, skriv bara in några punkter. I grund och botten skulle du kunna rita hela funktionen så här, om du provade ett oändligt antal kombinationer av siffror.
"Rita grafen för en funktion"
Оцените, пожалуйста статью