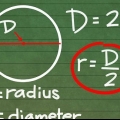
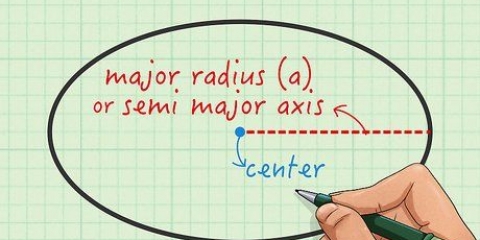
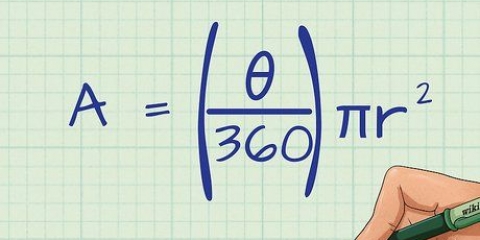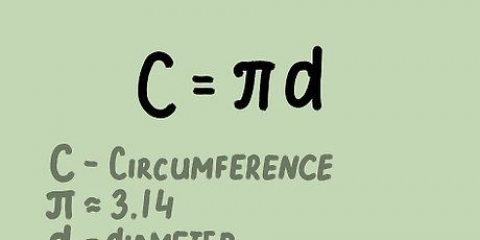Radien (r) av en cirkel är avståndet från en punkt på cirkeln till cirkelns mitt. diametern (d) av en cirkel är avståndet från en punkt på cirkeln till en annan punkt mittemot cirkeln, som går genom cirkelns centrum. Den grekiska bokstaven pi (π) står för förhållandet mellan omkretsen delat med diametern och representeras av talet 3,14159265..., ett irrationellt tal som varken har en slutsiffra eller ett igenkännbart mönster av upprepade siffror. Detta antal avrundas ofta till 3,14 för standardberäkningar. 
I de flesta matematiska problem anges radien eller diametern. 
Till exempel: Vad är omkretsen av en cirkel med en radie på 3 cm? Skriv formeln: C = 2πr Fyll i variablerna: C = 2π3 Multiplicera: C = (2*3*π) = 6π = 18,84 cm Till exempel: Vad är omkretsen av en cirkel med en diameter på 9 m? Skriv ner formeln: C = πd Fyll i variablerna: C = 9π Multiplicera: C = (9*π) = 28,26 m 
Bestäm omkretsen av en cirkel med en diameter på 5 m. C = πd = 5π = 15,7 m Bestäm omkretsen av en cirkel med en radie på 10 m. C = 2πr = C = 2π10 = 2 *10 *π = 62,8 m. 

Radien (r) av en cirkel är avståndet från en punkt på cirkeln till cirkelns mitt. diametern (d) av en cirkel är avståndet från en punkt på cirkeln till en annan punkt mittemot cirkeln, som går genom cirkelns centrum. Den grekiska bokstaven pi (π) står för förhållandet mellan omkretsen delat med diametern och representeras av talet 3,14159265..., ett irrationellt tal som varken har en slutsiffra eller ett igenkännbart mönster av upprepade siffror. Detta antal avrundas vanligtvis till 3,14 för grundläggande beräkningar. 
I de flesta matematiska problem anges radien eller diametern. 
Till exempel: vad är arean av en cirkel med en radie på 3 m? Skriv formeln: A = r. Fyll i variablerna: A = π3. Kvadra radien: r = 3 = 9 Multiplicera med pi: a = 9π = 28,26 m Till exempel: vad är arean av en cirkel med en diameter på 4 m? Skriv formeln: A = π(d/2). Fyll i variablerna: A = π(4/2). Dela diametern med 2: d/2 = 4/2 = 2 Kvaddra resultatet: 2 = 4 Multiplicera med pi: a = 4π = 12,56 m 
Hitta arean av en cirkel med en diameter på 7 m. A = π(d/2) = π(7/2) = π(3,5) = 12,25 * π= 38,47 m. Hitta arean av en cirkel med en radie på 3 m. A = πr = π * 3 = 9 * π = 28,26 m 

Till exempel: beräkna omkretsen av en cirkel med radien (x + 1). Skriv formeln: C = 2πr Fyll i den givna informationen: C = 2π(x+1) 
Till exempel: beräkna omkretsen av en cirkel med radien (x = 1). C = 2πr = 2π(x+1) = 2πx + 2π1 = 2πx +2π = 6,28x + 6,28 Om värdet på `x` anges senare i problemet kan du koppla in det och få ett heltal. 
Hitta arean av en cirkel med radien 2x. A = πr = π(2x) = π4x = 12,56x Hitta arean av en cirkel med diametern (x + 2). A = π(d/2) = π((x +2)/2) = ((x +2)/4)π
Beräkna omkretsen och arean av en cirkel
En cirkels omkrets (C) är dess omkrets, eller avståndet runt den. Arean (A) av en cirkel är hur mycket utrymme cirkeln upptar eller arean som omges av cirkeln. Både area och omkrets kan beräknas med enkla formler från cirkelns radie eller diameter och värdet på pi.
Steg
Del 1 av 3: Beräkna omkretsen

1. Lär dig formeln för en cirkels omkrets. Det finns två formler som kan användas för att beräkna en cirkels omkrets: C = 2πr eller C = d, där π är den matematiska konstanten och ungefär lika med 3,14,r är lika med radien och d lika med diametern.
- Eftersom radien på en cirkel är lika med två gånger dess diameter, är dessa ekvationer i huvudsak desamma.
- Enheterna för omkretsen kan vara vilken enhet som helst för längdmåttet: kilometer, meter, centimeter, etc.

2. Förstå de olika delarna av formeln. Det finns tre komponenter för att hitta en cirkels omkrets: radie, diameter och π. Radien och diametern är relaterade: radien är lika med halva diametern, medan diametern är lika med två gånger radien.

3. Mät cirkelns radie eller diameter. Placera en linjal på ena kanten av cirkeln, genom mitten och till andra sidan av cirkeln. Avståndet från cirkelns mitt är radien, medan avståndet från den andra änden av cirkeln är diametern.

4. Bearbeta och lösa variablerna. När du har bestämt cirkelns radie och/eller diameter kan du lägga in dessa variabler i lämplig ekvation. Om du har strålen, använd C = 2πr, men om du vet diametern så använd C = d.

5. Öva med några exempel. Nu när du har lärt dig formeln är det dags att öva med några exempel. Ju fler problem du löser, desto lättare blir det att lösa dem i framtiden.
Del 2 av 3: Beräkna area

1. Lär dig formeln för arean av en cirkel. Arean av en cirkel kan beräknas med antingen dess diameter eller dess radie, med två olika formler: A = r eller A = π(d/2), där π är den matematiska konstanten ungefär lika med 3,14,r radien och d diametern.
- Eftersom radien på en cirkel är lika med halva dess diameter, är dessa ekvationer i huvudsak desamma.
- Enheterna för area kan vara vilken enhet som helst för längd i kvadrat: km i kvadrat (km), kvadrat meter (m), kvadratcentimeter (cm), etc.

2. Förstå de olika delarna av formeln. Det finns tre komponenter för att hitta en cirkels omkrets: radie, diameter och π. Radien och diametern är relaterade till varandra: radien är lika med halva diametern, medan diametern är lika med dubbel radie.

3. Mät cirkelns radie eller diameter. Placera ena änden av en linjal vid en punkt på cirkeln, genom mitten och till den andra sidan av cirkeln. Avståndet från cirkelns mitt är radien, medan avståndet från den andra punkten på cirkeln är diametern.

4. Fyll i variablerna och lös dem. När du har bestämt cirkelns radie och/eller diameter kan du koppla in dessa variabler i lämplig ekvation. Om du känner till radien, använd A = r, men om du vet diametern så använd A = π(d/2).

5. Öva med några exempel. Nu när du har lärt dig formeln är det dags att öva med några exempel. Ju fler problem du löser, desto lättare blir det att lösa andra problem.
Del 3 av 3: Beräkna arean och omkretsen med variabler

1. Bestäm cirkelns radie eller diameter. Vissa problem ger en radie eller diameter med en variabel, till exempel r = (x + 7) eller d = (x + 3). I det här fallet kan du fortfarande bestämma arean eller omkretsen, men ditt slutliga svar kommer också att innehålla den variabeln. Skriv ner radien eller diametern som anges i uttalandet.
- Till exempel: beräkna omkretsen av en cirkel med radien (x = 1).

2. Skriv formeln med den givna informationen. Oavsett om du vill beräkna area eller omkrets följer du fortfarande de grundläggande stegen för att fylla i det du vet. Skriv formeln för area eller omkrets och fyll sedan i de givna variablerna.

3. Lös problemet som om variabeln vore ett tal. Vid det här laget kan du bara lösa problemet som du normalt skulle göra, och behandla variabeln som om den bara vore ett annat nummer. Du kan behöva använda fördelningsegendom för att förenkla det slutliga svaret.

4. Öva med några exempel. Nu när du har lärt dig formeln är det dags att öva med några exempel. Ju fler problem du löser, desto lättare blir det att lösa nya.
"Beräkna omkretsen och arean av en cirkel"
Оцените, пожалуйста статью