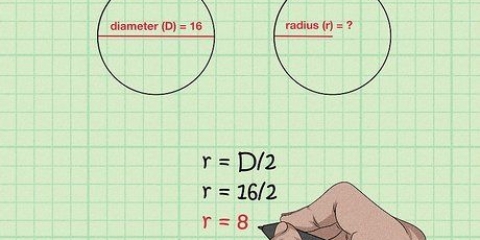
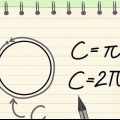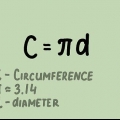Till exempel, om diametern på en cirkel är 4, är den raka 4/2 eller 2. 

Till exempel, om omkretsen är 15, är radien r = 15/2π, eller 2,39. 


a = √(3 + 4) a = √(9 + 16) a = √25 a = 5 
b= √(-7 + -6) b = √(49 + 36) b = √85 b = 9.23 
c= √(4 + 2) c = √(16 + 4) c = √20 c = 4.47 
Längden på triangeln är som följer: a = 5, b = 9.23 och c = 4.47. Så formeln för radien ser ut så här: r = (5 * 9.23*4.47)/(√(5 + 4.47 + 9.23)(4.47 + 9.23 - 5)(9.23 + 5 - 4.47)(5 + 4.47 – 9.23)). 
(a * b * c) = (5 * 9.23*4.47) = 206.29 r = (206.29)/(√(5 + 4.47 + 9.23)(4.47 + 9.23 - 5)(9.23 + 5 - 4.47)(5 + 4.47 – 9.23)) 
(a + b + c) = (5 + 4.47 + 9.23) = 18.7 (b + c - a) = (4.47 + 9.23 - 5) = 8.7 (c + a - b) = (9.23 + 5 - 4.47) = 9.76 (a + b - c) = (5 + 4.47 – 9.23) = 0.24 r = (206.29)/(√(18.7)(8.7)(9.76)(0.24)) 
(18.7)(8.7)(9.76)(0.24) = 381.01 r = 206.29/√381.01 
√381.01 = 19.51 r = 206.29/19.52 
r = 10.57
Beräkna radien av en cirkel
En cirkels radie är avståndet från cirkelns centrum till kanten. Diametern på en cirkel är längden på den räta linje som kan dras mellan två punkter på sfären eller cirkeln och genom dess centrum.Du blir ofta ombedd att beräkna radien för en cirkel baserat på andra data. I den här artikeln kommer du att lära dig hur du beräknar radien för en cirkel baserat på en given diameter, omkrets och area. Den fjärde metoden är en mer avancerad metod för att bestämma en cirkels centrum och radie baserat på koordinaterna för tre punkter på cirkeln.
Steg
Metod 1 av 3: Beräkna radien om du vet diametern

1. Kom ihåg vad diametern är. Diametern på en cirkel är längden på den räta linje som kan dras mellan två punkter på sfären eller cirkeln och genom dess centrum. Diametern är den längsta linjen som kan dras genom en cirkel och delar cirkeln i två halvor. Längden på diametern är också lika med längden på två gånger radien. Formeln för diametern är följande: D= 2r, där "d" står för diameter och "r" för balk. Formeln för radien kan härledas från föregående formel och är därför: r = D/2.

2. Dividera diametern med 2 för att hitta radien. Om du vet diametern på en cirkel behöver du bara dela den med 2 för att hitta radien.
Metod 2 av 3: Beräkna radien om du känner till omkretsen

1. Kommer du ihåg formeln för en cirkels omkrets?. En cirkels omkrets är avståndet runt cirkeln. Ett annat sätt att se på det är detta: omkretsen är längden på linjen du får om du skär upp cirkeln vid en punkt och lägger linjen rakt. Formeln för en cirkels omkrets är O = 2πr, där "r" är radien och π är konstanten pi, eller 3,14159... Formeln för radien är då r = O/2π.
- Vanligtvis kan du avrunda pi till två siffror efter decimalkomma (3,14), men kolla med din lärare först.

2. Beräkna radien med den angivna omkretsen. För att beräkna radien baserat på omkretsen dividerar du omkretsen med 2π eller 6,28
Metod 3 av 3: Beräkna radien om du känner till koordinaterna för tre punkter på cirkeln

1. Förstå att tre punkter kan definiera en cirkel. Alla tre punkter på ett rutnät definierar en cirkel som tangerar de tre punkterna. Det är den omskrivna cirkeln i triangeln som bildar punkterna. Cirkelns centrum kan falla innanför eller utanför triangeln, beroende på positionen för de tre punkterna, och samtidigt är det "genomskärning" av triangeln.Det är möjligt att beräkna cirkelns radie om du känner till xy-koordinaterna för de tre punkterna i fråga.
- Som ett exempel, låt oss ta tre punkter definierade enligt följande: P1 = (3,4), P2 = (6, 8) och P3 = (-1, 2).

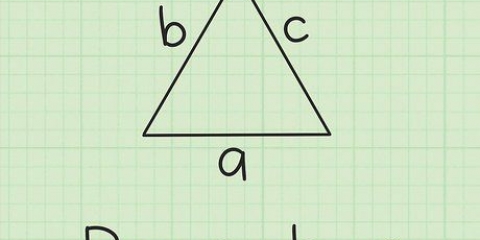
2. Använd avståndsformeln för att beräkna längden på de tre sidorna av triangeln, som vi kallar a, b och c. Formeln för avståndet mellan två koordinater (x1, y1) och (x2, y2) är som följer: avstånd = √(( x2 - X1) + (y2 - y1)). Bearbeta nu koordinaterna för de tre punkterna i denna formel för att hitta längderna på triangelns tre sidor.

3. Beräkna längden på den första sidan a, som går från punkt P1 till P2. I vårt exempel är koordinaterna för P1 (3.4) och P2 (6.8), så längden på sidan a = √((6 - 3) + (8 - 4)).

4. Upprepa processen för att hitta längden på den andra sidan b, som går från P2 till P3. I vårt exempel är koordinaterna för P2 (6,8) och för P3 (-1,2), så längden på sidan b = √((-1 - 6) + (2 - 8)).

5. Upprepa processen för att hitta längden på den tredje sidan c, som går från P3 till P1. I vårt exempel är koordinaterna för P3 (-1,2) och P1 (3,4), så längden på sidan c =√((3 - -1) + (4 - 2)).

6. Använd dessa längder i formeln för att hitta radie: (abc)/(√(a + b + c)(b + c - a)(c + a - b)(a + b - c)).. Resultatet är radien för vår cirkel!

7. Multiplicera först de tre längderna tillsammans för att hitta täljaren för bråket. Sedan justerar du formeln.

8. Beräkna summorna inom parentes. Placera sedan resultaten i formeln.

9. Multiplicera värdena i nämnaren.

10. Ta kvadratroten av produkten för att hitta bråkets nämnare.

11. Dela nu täljaren med nämnaren för att hitta cirkelns radie!
"Beräkna radien av en cirkel"
Оцените, пожалуйста статью