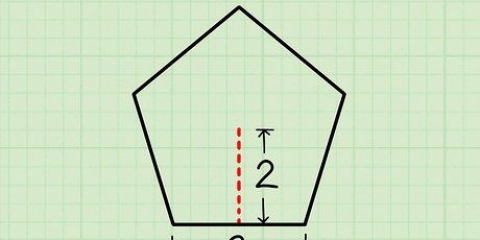
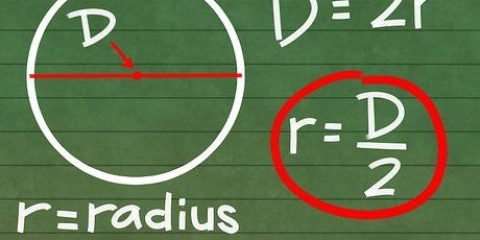
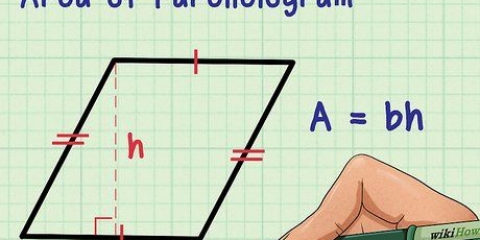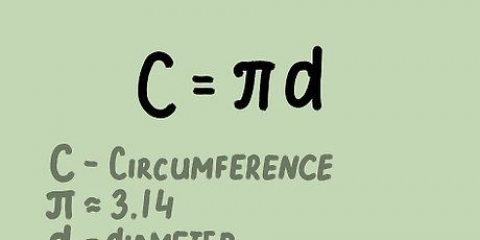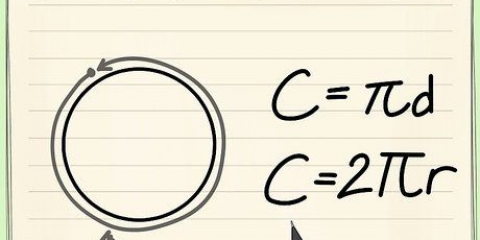Du arbetar nu med en liksidig triangel eftersom alla tre sidor av figuren har exakt samma längd. Men kom ihåg att denna formel gäller för alla trianglar. 
Ett annat exempel: Om a = 4, b = 3, och c=5, då är omkretsen 3 + 4 + 5, med andra ord 12. 
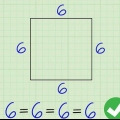
I det här exemplet är alla sidorna 5 cm, så det korrekta svaret är 15 cm. 



Till exempel, om du kan det siden a = 3 och siden b = 4, skriv det sedan i formeln så här: 3 + 4 = c. Ett andra exempel: Om du vet att längden på sidana = 6, och hypotenusan c = 10, så lägger du in det i ekvationen så här: 6 + b = 10. 
I det första exemplet multiplicerar du värdena 3 + 4 = c och du upptäcker det och 25= c. Räkna sedan ut kvadratroten ur 25 så att du kommer fram till c = 25. I det andra exemplet multiplicerar du värdena 6 + b = 10 och det upptäcker du 36 + b = 100.Subtrahera 36 från 100 för att få b = 64, och räkna sedan ut kvadratroten ur 64, så att du får b = 8. 
I det första exemplet vill säga X = 3 + 4 + 5, eller 12. I det andra exemplet, dvs X = 6 + 8 + 10 eller 24. 

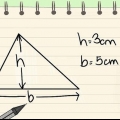
Föreställ dig till exempel en triangel med sidan 10 och en av 12 och en vinkel på 97° mellan dem. Vi skriver sedan variablerna så här:a = 10, b = 12, C = 97°. 
c = 10 + 12 - 2 × 10 × 12 × cos(97). c = 100 + 144 – (240 × -0,12187)(Runda cosinus till 5 siffror efter decimalkomma) c = 244 – (-29,25) c = 244 + 29,25(Ta minustecknet om cos(C) är negativ!) c = 273,25 c = 16,53 
I vårt exempel: 10 + 12 + 16,53 = 38,53, det är omkretsen av vår triangel!
Beräkna omkretsen av en triangel
Omkretsen av en triangel är längden på en linje som kan dras längs triangelns sidor. Det enklaste sättet är att lägga ihop längderna på alla sidor, men om du inte kan alla längder måste du räkna ut dem först. Den här artikeln lär dig först hur du beräknar omkretsen av en triangel om du vet längden på alla tre sidorna; detta är den enklaste och mest använda metoden. Sedan får du lära dig hur du beräknar omkretsen om du bara kan längden på två av de tre sidorna. Slutligen förklarar det hur man beräknar omkretsen om du känner till längden på två sidor och vinkeln mellan dem, med hjälp av cosinuslagen.
Steg
Metod 1 av 3: Beräkna omkretsen av en triangel om längden på alla sidor är givna

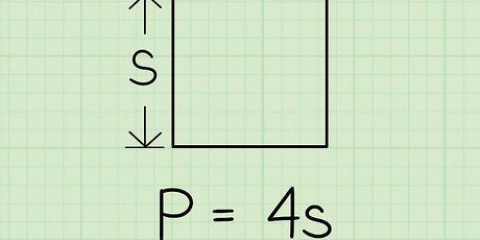
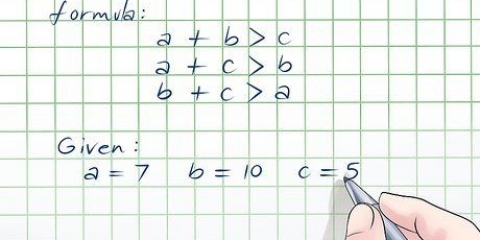
1. Lär dig formeln för att hitta omkretsen. Formeln är: A + B + C = X varigenom a, B, och C representerar längderna på sidorna och X omkretsen.
- Denna formel betyder i princip att för att hitta omkretsen av en triangel måste du lägga ihop längderna på de tre sidorna.

2. Bestäm längden på alla tre sidorna. I det här exemplet: a = 5, B = 5, C = 5.

3. Lägg ihop längderna på de tre sidorna. I det här exemplet: 5 + 5 + 5 = 15. Så omkretsen av triangeln (X) är 15.

4. Kom ihåg att alltid ta med enheterna i ditt svar. Om sidorna anges i centimeter, måste ditt slutliga svar också anges i centimeter. Om sidorna ges i termer av en variabel, till exempel x, måste svaret också vara i termer av x.
Metod 2 av 3: Beräkna omkretsen om endast två sidor av triangeln ges

1. Vet vad en rätvinklig triangel är. En rät triangel är en triangel med en rät vinkel (90 grader). Sidan av triangeln mittemot den räta vinkeln är alltid den längsta sidan, vilket kallas hypotenusan eller hypotenusan. Rättvinklade trianglar dyker upp regelbundet i matteprov, men som tur är finns det en mycket praktisk formel för att beräkna längden på okänd sida!

2. Känna till Pythagoras sats. Pythagoras sats gäller för vilken rätvinklig triangel som helst och lyder: a² + b² = c².

3. Titta på din triangel och skriv vid sidorna a, b och c. Kom ihåg att den längsta sidan kallas hypotenusan. Den ligger mitt emot rät vinkel, och du måste gå till denna sida c att skriva. På de två kortare sidorna skriver du a och b. Det spelar ingen roll vilken du placerar var, resultatet blir detsamma!

4. Ta längden på sidorna i Pythagoras sats. Kom ihåg det a + b = c. Fyll i längderna i stället för motsvarande bokstäver.

5. Lös ekvationen för att hitta den saknade längden. Du måste först multiplicera de kända sidorna med sig själva (till exempel 3 = 3 * 3 = 9).Om du letar efter hypotenusan kan du sedan lägga till de två värdena tillsammans och beräkna kvadratroten av resultatet för att hitta längden. Om du saknar en annan sida måste du subtrahera de två och sedan beräkna kvadratroten av resultatet för att hitta längden.

6. Lägg till längderna på de tre sidorna tillsammans för att beräkna omkretsen. Kom ihåg ekvationen: X = a + b + c. Nu när du vet längderna på sidornaa, b och c vet att du kan lägga ihop dem för att få omkretsen.
Metod 3 av 3: Hitta omkretsen av en triangel med hjälp av cosinuslagen

1. Lär dig lagen om cosinus. Med hjälp av cosinuslagen kan du lösa vilken triangel som helst om du vet längden på två sidor och vinkeln mellan dem. Det fungerar för alla triangel, och det är en mycket användbar formel. Cosinuslagen säger att för alla triangel med sidor a, b, och c, med motsatta hörna, B, och C följande formel gäller:c = a + b - 2ab cos(C).

2. Titta på din triangel och sätt bokstäverna vid de olika delarna. Den första sidan vet du att du måste a kalla det, och den motsatta vinkeln är då a. Den andra sidan vet du att du måste b ring det motsatta hörnet B. Den vinkel du vet att du måste C kalla det, och den tredje sidan, den du vill lösa, är då c.

3. Lägg din information i ekvationen och lös sidan c. Du måste först multiplicera a och b med sig själva och lägga ihop dem. Beräkna sedan cosinus för C med cos-funktion på din miniräknare eller en onlineräknare. Multiplicera cos(C) av 2ab och subtrahera resultatet från summan av a + b.Svaret är c.Beräkna kvadratroten av detta och du vet längden på sidan c.I vårt exempel:

4. Använd längden påc för att beräkna omkretsen av din triangel. Kom ihåg att formeln för omkretsen är: X = a + b + c, så du behöver bara lägga ihop alla längder eftersom a och b visste du.Lätt som en plätt!
"Beräkna omkretsen av en triangel"
Оцените, пожалуйста статью