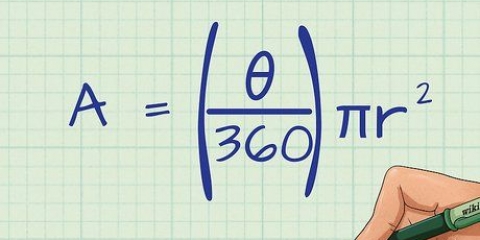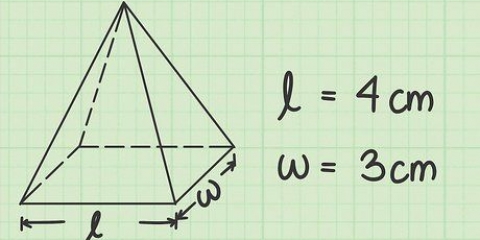För att hitta s³, multiplicera s tre gånger med sig själv: s³ = s x s x s 
Om du inte är 100 % säker på om din form är en kub, mät alla sidor för att se om de är lika. Om de inte är det måste du använda metoden nedan för att beräkna volymen på en stråle. Obs: I exempelbilderna anges måtten i tum (in), men vi använder centimeter (cm). 




Exempel: Längden på denna balk är 4 cm, så l = 4 cm. Oroa dig inte för mycket om vilken sida som är längden osv. Så länge du bara mäter tre olika sidor blir resultatet detsamma. 
Exempel: Bredden på denna balk är 3 cm, så b = 3 cm. Om du mäter strålen med linjal eller måttband, glöm inte att skriva ner allt i samma måttenhet. 
Exempel: Höjden på denna stav är 6 cm, så h = 6 cm. 
I det här exemplet är l = 4, b = 3 och h = 6. Därför är utfallet V = 4 x 3 x 6 = 72. 
Om till exempel balkens mått var i meter skulle du få l = 2 m, w = 4 m och h = 8 m. Volymen blir då 2 m x 4 m x 8 m = 64 m³. 

I de flesta fall räcker det att avrunda pi till 3,14. Fråga din lärare vad han/hon vill. Formeln för att hitta volymen av en cylinder är faktiskt mycket lik den för volymen av en balk: du multiplicerar höjden på formen med arean av basen. För en stråle är basens area l x b, för en cylinder är det π x r², arean av en cirkel med radien r. 

Ett annat alternativ är att mäta cirkelns omkrets (avståndet runt den) med en bit snöre eller ett måttband. Lägg sedan in resultatet i denna formel: C (omkrets) är 2 x π x r. Dividera omkretsen med 2 x π (6.28) så har du radien. Om till exempel omkretsen du mätte är 8 cm, är radien 1,27 cm. Om du verkligen behöver en exakt mätning kan du använda båda metoderna för att se om resultaten är desamma. Om inte, kolla igen. Omkretsmetoden ger vanligtvis ett mer exakt resultat. 
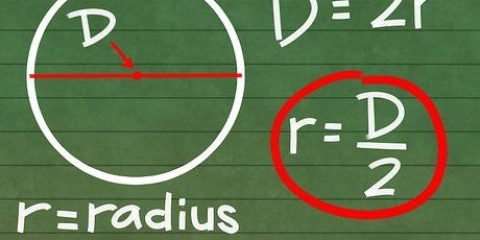
Om radien är 4 cm är cirkelns yta A = π x 4². 4² = 4 x 4, eller 16. 16 xπ = 16 x 3,14 = 50,24 cm². Om diametern på basen är känd, snarare än radien, kom ihåg att d = 2 x r. Sedan måste du dela diametern med två för att hitta radien. 

V = π x 4² x 10 π x 4²= 50,24 50,24 x 10 = 502,4 V = 502,4 


Formeln för raka pyramider, där spetsen är direkt ovanför mitten av basen, är densamma som för lutande pyramider, där spetsen inte är i mitten. 
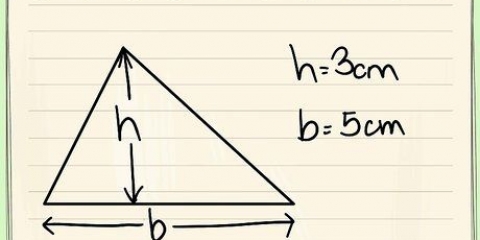
Formeln för arean av en triangel är A = 1/2 x b x h, där b är basen och h är höjden. Det är möjligt att beräkna arean av vilken vanlig polygon som helst med formeln A = 1/2 xpxa, där A är arean, p är omkretsen och a är apotem, vilket är avståndet från formens centrum till mitten av en av sidorna. Du kan också göra det enkelt för dig själv och använda en vanlig polygonkalkylator online. 

Om vi hade haft en annan pyramid med en bas med arean 26 och höjden 8, skulle resultatet ha blivit: 1/3 x 26 x 8 = 69,33. 


Delen π x r² hänvisar till arean av cirkeln som bildar konens bas. Så formeln för konens volym är 1/3 x b x h, precis som formeln för pyramiden i metoden ovan! 
I detta exempel är radien 3 cm. Om vi sätter det i formeln får vi: A = π x 3². 3² = 3 x3, eller 9, så A = π x 9. A = 28,27 cm². 


I vårt exempel är det 141,35 x 1/3 = 47,12, konens volym. Återigen: 1/3 x π x 3² x 5 = 47,12. 




Om du till exempel mäter bollen och ser att omkretsen är 18 cm, dividera det med 6,28, du vet att radien är 2,87 cm. Det kan vara knepigt att mäta en sfär, så det är bäst att mäta den tre gånger och göra ett medelvärde (lägg ihop de tre måtten och dividera med tre) för att få mätningen så exakt som möjligt. Om du till exempel mätte tre gånger och resultaten var 18 cm, 17,75 cm och 18,2 cm, lägg till det tillsammans (18 + 17,5 + 18,2 = 53,95) och dividera med 3 (53,95/3 = 17,98). Du använder detta medelvärde när du beräknar volymen. 


Så i vårt exempel blir det 36 x 3,14 = 113,09. 
Beräkna volym
Volymen av en figur är det tredimensionella utrymme figuren upptar. Du kan representera volym som mängden vatten (eller luft, sand, etc.).) som skulle passa formen om den var helt full. Vanligt använda måttenheter för volym är kubikcentimeter och kubikmeter.Den här artikeln kommer att lära dig hur du beräknar volymen av sex olika tredimensionella former som vanligtvis stöter på i matematiktest, inklusive kuben, sfären och konen. Du kommer att se att det finns många likheter som gör det lätt för dig att komma ihåg. Se om du kan hitta de matcherna!
Steg
Metod 1 av 6: Beräkna volymen av en kub

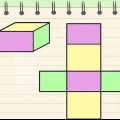
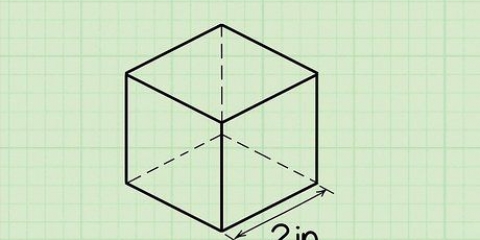
1. Känn igen en kub. En kub är en tredimensionell form med sex identiska fyrkantiga ytor.Det är med andra ord en låda med lika sidor överallt.
- En tärning är ett bra exempel på en kub du kan ha hemma. Sockerbitar eller barnblock är ofta kuber också.

2. Lär dig formeln för att beräkna volymen på kuben. Eftersom alla längder på kubens sidor är lika långa är formeln för att beräkna kubens volym mycket enkel. Platsen där två sidor möts kallas revbenet. Vi förkortar volym till "V". Revbenen, eller längden på sidan, kallar vi här "s". Formeln blir då V = s³

3. Hitta längden på ena sidan av kuben. Beroende på uppdraget kan denna information redan finnas där, men du kan också behöva mäta den själv med en linjal. Kom ihåg att eftersom det är en kub ska alla längder på sidorna vara lika, så det spelar ingen roll vilken du mäter.

4. Sätt längden på sidan i formeln V = s³ och beräkna den. Om du till exempel mätte att sidolängden på din kub är 5 cm, skulle du skriva formeln så här: V = (5)³. 5 x 5 x 5 = 125 cm³, så det är volymen på din kub!

5. Se till att du skriver ditt svar i kubikcentimeter. I exemplet ovan mättes kuben i centimeter, så svaret måste ges i kubikcentimeter. Om längden på sidan av kuben hade varit 3 meter, skulle volymen ha varit V = (3 m)³ = 27 m³.
Metod 2 av 6: Beräkna volymen av en stråle.

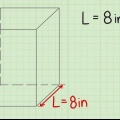
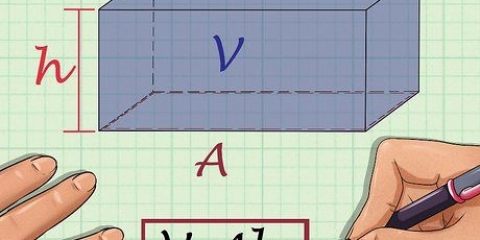
1. Känn igen en stråle. En balk är en figur som består av sex rektangulära ytor. Så det är faktiskt en tredimensionell rektangel, en sorts låda.
- Egentligen är en kub bara en speciell stråle, där alla sidor är lika.

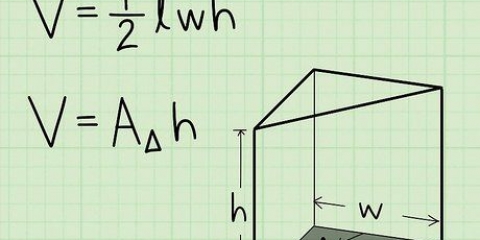
2. Lär dig formeln för att beräkna volymen av en stråle. Formeln för en stråles volym är V = längd (l) x bredd (w) x höjd (h), eller V = l x b x h. Obs: Bilderna som medföljer dessa exempel visar "w" för bredd.

3. Hitta längden på balken. Längden är den längsta sidan av balken som är parallell med marken eller ytan den vilar på. Längden kan redan anges på bilden, eller så måste du kanske mäta den med en linjal.

4. Hitta strålens bredd. Balkens bredd kan hittas genom att mäta kortsidan som är parallell med marken eller ytan som den vilar på. Återigen, kontrollera först om det redan är indikerat på bilden, och mät det annars med din linjal.

5. Hitta höjden på strålen. Höjd är avståndet från marken eller ytan som balken vilar på till toppen av balken. Se om det redan visas på bilden och mät det annorlunda med din linjal eller måttband.

6. Ange måtten i formeln och beräkna den. Kom ihåg att V = l x b x h.

7. Var noga med att skriva ditt svar i kubikcentimeter. Resultatet blir därför 72 kubikcentimeter, eller 72 cm³.
Metod 3 av 6: Beräkna volymen av en cylinder

1. Lär dig att identifiera en cylinder. En cylinder är en tredimensionell form med två identiska runda ändar förbundna med en enda krökt sida. Det är faktiskt ett rakt, runt spö.
- En burk är ett bra exempel på en cylinder eller ett AA-batteri.

2. Memorera formeln för volymen av en cylinder. För att beräkna volymen på en cylinder måste du känna till dess höjd och radien på dess cirkulära bas.Radien är avståndet från cirkelns centrum till kanten. Formeln är V =π x r² x h, där V är volymen, r är radien, h är höjden och π är konstanten pi.

3. Hitta basens radie. Om det redan finns angivet på bilden är det bara att fylla i det. Om du fick diametern istället för radien, dividera den med 2 för att hitta radien (d = 2 x r).

4. Mät formen om radien inte anges. Observera att det kan vara svårt att mäta den exakta radien på en cirkel. Ett alternativ är att mäta cirkeln på dess bredaste punkt med din linjal uppifrån och ned, dividera den med två.

5. Beräkna arean av cirkeln vid basen. Sätt radien i formeln π x r². Multiplicera radien med sig själv och multiplicera resultatet med π. Till exempel:

6. Hitta cylinderns höjd. Detta är helt enkelt avståndet mellan de två cirkulära baserna, eller avståndet från ytan som cylindern vilar på till toppen av cylindern. Se om längden redan är angiven på bilden, eller mät den annorlunda med din linjal eller måttband.

7. Multiplicera arean av basen med cylinderns höjd för att hitta volymen. Sätt värdena i formeln V =π x r² x h. I vårt exempel med en radie på 4 cm och en höjd på 10 cm:

8. Kom ihåg att skriva ditt svar i kubikcentimeter. I det här exemplet mättes cylindern i centimeter, så svaret måste skrivas i kubikcentimeter: V = 502,4cm³. Om cylindern mättes i meter, skulle volymen behöva skrivas i kvadratmeter (m³).
Metod 4 av 6: Beräkna volymen av en vanlig pyramid

1. Vet vad en vanlig pyramid är. En pyramid är en tredimensionell form med en polygon vid basen och sidorna som smalnar av mot toppen (spetsen på pyramiden).En vanlig pyramid är en pyramid vars bas är en vanlig polygon, vilket betyder att alla sidor och vinklar i denna polygon är lika.
- Vanligtvis är en pyramid avbildad med en kvadratisk bas och sidor som avsmalnar till en spets, men basen av en pyramid kan faktiskt ha 5, 6 eller 100 sidor!
- En pyramid med en cirkel som bas kallas en kon, vilket vi kommer att diskutera i nästa metod.

2. Lär dig formeln för att beräkna volymen av den vanliga pyramiden. Formeln för volymen av en vanlig pyramid är V = 1/3 x b x h, där b är arean av basen och h är höjden på pyramiden, eller det vertikala avståndet från basen till toppen.

3. Beräkna arean av basen. Formeln för detta beror på antalet sidor av basen. I vårt exempel är basen en kvadrat med sidor på 6 cm. Kom ihåg att formeln för att beräkna arean av en kvadrat är A = s². Så med vår pyramid är det 6 x 6 = 36 cm².

4. Hitta höjden på pyramiden. I de flesta fall kommer det att indikeras på bilden. I vårt exempel är höjden på pyramiden 10 cm.

5. Multiplicera arean av pyramidens bas med höjden och dividera med 3 för att hitta volymen. Kom ihåg att formeln är V = 1/3 x b x h. I vårt exempel har pyramiden en bas med arean 36 och höjden 10, så volymen är 36 x 10 x 1/3 = 120.

6. Kom ihåg att skriva utfallet i kubikenheter. Måtten på pyramiden i exemplet angavs i centimeter, så resultatet måste skrivas i kubikcentimeter, 120 cm³. Om måtten angavs i meter, skriv svaret i kubikmeter (m³).
Metod 5 av 6: Beräkna volymen av en kon

1. Lär dig vilka egenskaper en kon har. En kon är en tredimensionell form med en cirkulär bas och en enda punkt på den motsatta sidan. Ett annat sätt att se en kon är att det är en speciell sorts pyramid med en cirkulär bas.
- Om spetsen av konen är direkt ovanför mitten av basen, kallas det en rak kon. Om det inte är direkt ovanför mitten kallas det en sned kon. Lyckligtvis är formeln för att beräkna volymen densamma för båda typerna av koner.

2. Känna till formeln för att beräkna konens volym. Denna formel är V = 1/3 x π x r² x h, där r är radien på cirkeln vid basen, h är höjden på könen och π är konstanten pi, som kan avrundas till 3,14.

3. Beräkna arean av konens cirkulära bas. För att göra detta måste du känna till basens radie, som bör anges på din bild. Om du fick diametern istället för radien, dividera bara det talet med 2, eftersom diametern är 2 gånger radien (d = 2 x r). Sätt sedan radien i formeln A = π x r² för att beräkna arean.

4. Hitta höjden på konen. Detta är det vertikala avståndet från konens bas till toppen. I vårt exempel är höjden på konen 5 cm.

5. Multiplicera höjden på konen med arean av basen. I vårt exempel är basytan 28,27 cm² och höjden 5 cm, så b x h = 28,27 x 5 = 141,35.

6. Multiplicera nu detta resultat med 1/3 (eller dividera med 3) för att få konens volym. I steget ovan beräknade vi faktiskt volymen av en cylinder, det vill säga en kon där väggarna skulle stå upprätt och hamna i en annan cirkel. Att dividera den med 3 ger dig konens volym.

7. Kom ihåg att skriva utfallet i kubikenheter. Vår kon mättes i centimeter, så volymen bör uttryckas i kubikcentimeter: 47,12 cm³.
Metod 6 av 6: Beräkna volymen av en sfär

1. Känn igen en sfär. En sfär är en perfekt rund tredimensionell form, där varje punkt på dess yta är lika långt från mitten. Det är med andra ord en boll.

2. Lär dig formeln för att beräkna volymen av en sfär. Formeln är V = 4/3 x π x r³ (dvs: "fyra tredjedelar pi gånger kubik r"), där r är sfärens radie och π är konstanten pi (3.14).

3. Hitta sfärens radie. Om radien redan är angiven på bilden är det enkelt. Med tanke på diametern, dividera detta tal med 2 för att få radien. Sfärens radie i detta exempel är 3 centimeter.

4. Mät sfären om radien inte anges. Om du behöver mäta en sfär (som en tennisboll) för att hitta radien, hitta en sträng som är tillräckligt lång för att linda hela vägen runt den. Linda den sedan runt föremålet på den bredaste punkten och markera punkten där strängen åter sammanfogas. Mät sedan denna del av snöret med en linjal för att veta omkretsen av sfären. Dividera det med 2 x π, eller 6,28, så vet du radien.

5. Höj radien till tredje potens för att hitta r³. Att höja till tredje potens innebär helt enkelt att multiplicera talet tre gånger med sig självt, så r³ = r x r x r. I vårt exempel blir r=3 3 x 3 x 3 = 27.

6. Multiplicera ditt svar med 4/3. Du kan göra det med en miniräknare, eller bara göra det själv och förenkla bråket. I vårt exempel är det 27 x 4/3 = 180/3, eller 36.

7. Multiplicera resultatet med π för att hitta sfärens volym. Det sista steget i att beräkna volymen är att multiplicera resultatet hittills med π. Runda av π till två decimaler, det räcker för de flesta matematiska problem (om inte din lärare säger något annat), så multiplicera det med 3,14 så har du svaret.

8. Skriv ditt svar i kubikenheter. I vårt exempel mätte vi i centimeter, så svaret är V = 113,09 cm³.
Оцените, пожалуйста статью