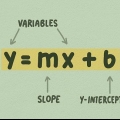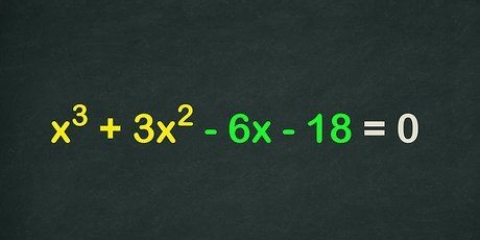Instrucțiuni gratuite pas cu pas 
Om (lutnings)koefficienten a i ekvationen är positiv, öppnar parabeln uppåt (i en vertikalt orienterad parabel), om den stora bokstaven är `U` och vertex är ett minimum. Som den a negativ, parabeln öppnar sig nedåt och vertexet har ett maximum. Om du har problem med att komma ihåg detta, tänk på det så här: en ekvation med a positivt a ser ut som ett leende; en jämförelse med en negativ a ser ut som en rynka pannan. Låt oss säga att du har följande ekvation: y = 2x -1. Denna parabel är formad som ett "U" eftersom a (2) är positivt. Om ekvationen har en y-term istället för en x-term i andra potensen, kommer parabeln att vara horisontellt orienterad och öppen i sidled (till höger eller vänster), som ett `C` eller ett bakåt `C`. Till exempel: parabeln y = x + 3 öppnas till höger, som ett `C`. 
I exemplet ovan (y = 2x² -1), är a = 2 och b = 0`.` Nu kan du beräkna symmetriaxeln genom att fylla i siffrorna:x = -0 / (2)(2) = 0`.` I detta fall är symmetriaxeln x = 0 (det vill säga koordinatsystemets y-axel). 
Koordinaterna för vertex kallas också (h, k). I detta fall h lika med 0 och k lika med -1. Parabolens ekvation kan skrivas i formen y = a(x - h)² + k. I det här formuläret är vertex punkten (h, k) och du behöver inte göra några beräkningar för att hitta vertex annat än korrekt tolkning av grafen. 
Det mellersta värdet på x måste vara symmetriaxeln i fallet med en "vertikal" parabel. Du måste inkludera minst två värden över och under mittvärdet för x i tabellen för symmetri. I det här exemplet placerar du värdet på symmetriaxeln (x = 0) i mitten av tabellen. 
om x = -2, sedan y: y = (2) (-2) - 1 = 8 - 1 = 7 om x = -1, sedan y: y = (2) (-1) - 1 = 2 - 1 = 1 om x = 0, sedan y: y = (2) (0) - 1 = 0 - 1 = -1 om x = 1, sedan y: y = (2) (1) - 1 = 2 - 1 = 1 om x = 2, sedan y: y = (2) (2) - 1 = 8 - 1 = 7 
X-axeln är horisontell, y-axeln är vertikal. De positiva talen på y-axeln är ovanför och de negativa talen under punkten (0, 0). De positiva talen på x-axeln är till höger och de negativa talen till vänster om punkten (0, 0). 
Rita en parabel
En parabel är en tvådimensionell, spegelsymmetrisk kurva som har formen av en båge. Varje punkt på parabeln är på samma avstånd från en fast punkt (fokus) och en fast rät linje (riktlinjen). För att kartlägga en parabel måste du hitta toppen av parabeln, samt några punkter på vardera sidan av den, för att markera vägen punkterna färdas.
Steg
Del 1 av 2: Rita en parabel
1. Förstå delarna av en parabel. Du kan få lite information innan du börjar, och att känna till terminologin hjälper dig att undvika onödiga steg. Här är de delar av parabeln du behöver känna till:
- Fokuset. En fast punkt på insidan av parabeln som används för den formella definitionen av kurvan.
- regissören. En solid, rak linje. Parabeln är den plats eller uppsättning punkter där en given punkt är lika långt från fokus och den direktrix ligger. (Se diagrammet ovan.)
- Symmetriaxeln. Detta är en rät linje som går genom parabelns vertex och på samma avstånd från motsvarande punkter på parabelns två armar.
- vertexet. Punkten där symmetriaxeln skär parabeln kallas parabelns vertex. Om parabeln öppnar sig eller åt höger är vertex a minimum av kurvan. Om parabeln öppnar sig nedåt eller till vänster är vertex a maximal.
2. Känna till ekvationen för en parabel. Den allmänna ekvationen för en parabel är y = ax+ bx + c. Det kan också skrivas i den ännu mer allmänna formen y = a(x – h)² + k, men vi kommer här att fokusera på den första formen av ekvationen.
3. Hitta symmetriaxeln. Kom ihåg att symmetriaxeln är den räta linjen som går genom parabelns vändpunkt (vertex). När det gäller en vertikal parabel (dal eller berg) är axeln densamma som spetsens x-koordinat, det vill säga x-värdet för den punkt där symmetriaxeln skär parabeln. Använd den här formeln för att hitta symmetriaxeln: x = -b/2a.
4. Hitta spetsen. När du väl känner till symmetriaxeln kan du koppla in det värdet för x för att få y-koordinaten. Dessa två koordinater ger dig parabelns vertex. I det här fallet ersätter du 0 med 2x -1 för att få y-koordinaten. y = 2 x 0-1 = 0-1 = -1. Toppunkten är (0,-1) och parabeln skär y-axeln vid -1.
5. Skapa en värdetabell för x. Skapa en tabell med vissa värden för x i den första kolumnen. Den här tabellen ger dig de koordinater du behöver för att rita en graf av ekvationen.
6. Beräkna värdena för motsvarande y-koordinater. Ersätt valfritt värde på x i parabelns ekvation och beräkna motsvarande värden på y. Lägg dessa beräknade värden på y i tabellen. I det här exemplet beräknas värdena för y enligt följande:
7. Ange de beräknade värdena för y i tabellen. Nu har du hittat minst fem koordinatpar för parabeln, och du är nästan redo att rita parabeln. Baserat på ditt arbete har du nu följande poäng: (-2, 7), (-1, 1), (0, -1), (1, 1), (2, 7). Kom ihåg att parabeln (symmetrisk) representeras med avseende på symmetriaxeln. Detta betyder att y-koordinaterna för punkterna mitt emot varandra med avseende på symmetriaxeln blir lika. Y-koordinaterna associerade med x-koordinaterna -2 och +2 är båda 7; y-koordinaterna som hör till x-koordinaterna -1 och +1 är båda 1, och så vidare.
8. Rita tabellpunkterna i koordinatsystemet. Varje rad i tabellen bildar ett koordinatpar (x, y) på koordinatsystemet. Rita alla punkter med hjälp av koordinaterna i tabellen.
9. Koppla ihop prickarna. För att plotta parabeln, koppla ihop punkterna som ritades i föregående steg. Grafen i detta exempel ser ut som ett U. Anslut prickarna med lätt böjda (snarare än raka) linjer. Detta skapar den mest exakta bilden av parabeln (som är lätt krökt över hela sin längd). I vardera änden av parabeln kan du rita pilar som pekar bort från vertexet, om du vill. Detta indikerar att parabeln fortsätter på obestämd tid.
Del 2 av 2: Flytta grafen för en parabel
Om du vill ha ett snabbare sätt att skifta en parabel utan att behöva hitta dess vertex igen och specificera om olika punkter på parabeln, måste du förstå ekvationen för en parabel och lära dig att omvandla den vertikalt eller horisontellt. Börja med den grundläggande parabeln: y = x. Den har en vertex vid punkten (0, 0) och är en dalparabel. Några punkter i grafen är: (-1, 1), (1, 1), (-2, 4) och (2, 4). Du kan skifta en parabel baserat på ekvationen.
1. Flytta en parabel uppåt. Tänk på ekvationen y = x +1. Detta flyttar den ursprungliga parabeln upp med en enhet. Toppunkten är nu (0, 1) istället för (0, 0). Dess form har inte ändrats, men varje y-koordinat kommer att flyttas upp en enhet. Så istället för (-1, 1) och (1, 1) ritar vi punkterna (-1, 2) och (1, 2).
2. Flytta ner en parabel. Ta ekvationen y = x -1. Vi flyttar den ursprungliga parabeln ned med en enhet så att vertex nu är (0, -1) istället för (0, 0,). Den kommer fortfarande att ha samma form som den ursprungliga parabeln, men varje y-koordinat kommer att flyttas ned en enhet. Så istället för (-1, 1) och (1, 1) ritar vi till exempel (-1, 0) och (1, 0).
3. Flytta en parabel åt vänster. Tänk på ekvationen y = (x + 1). Detta förskjuter den ursprungliga parabeln en enhet åt vänster. Toppunkten är nu (-1, 0) istället för (0, 0). Formen på den ursprungliga parabeln förblir densamma, men varje x-koordinat förskjuts en åt vänster. Till exempel, istället för (-1, 1) och (1, 1), ritar vi (-2, 1) och (0, 1).
4. Flytta en parabel åt höger. Tänk på ekvationen y = (x - 1). Detta är den ursprungliga parabeln förskjuten en enhet åt höger. Toppunkten är nu (1, 0) istället för (0, 0). Formen på den ursprungliga parabeln förblir densamma, men varje x-koordinat förskjuts en plats åt höger. Till exempel, istället för (-1, 1) och (1, 1), ritar vi (0, 1) och (2, 1).
Оцените, пожалуйста статью
