Antag i vårt exempel att massan på 10 kg hänger på ett rep, som inte är fäst vid en balk, utan används för att lyfta upp massan med en acceleration på 1 m/s. I fall som detta måste vi inte bara ta hänsyn till accelerationen på massan, utan även gravitationskraften, genom att lösa detta på följande sätt: ft = Fg + m × a ft = 98 + 10 kg × 1 m/s ft = 108 Newton. 
Eftersom riktningen och storleken på centripetalkraften ändras när föremålet på repet rör sig och hastigheten ändras, ändras också den totala spänningen i repet, som alltid drar parallellt med repet mot mittpunkten. Kom ihåg att gravitationskonstanten drar på föremålet. Så om ett föremål kastas runt i vertikalt läge är den totala spänningen största längst ner på objektets bana (i fallet med en pendelklocka kallas detta även för jämvikt), där objektet rör sig snabbast. Spänningen är minst i toppen av den cirkulära rörelsen, där hastigheten är lägst. Antag i exemplet att föremålet svänger som en pendel. Repet är 1,5 meter långt och massan rör sig med en hastighet av 2 m/s på den lägsta punkten. Om vi vill beräkna spänningen vid den punkten, den punkt där hastigheten är högst, måste vi först se att spänningen på grund av gravitationen vid denna punkt är densamma som när pendeln är i vila - 98 Newton. För att hitta centripetalkraften, beräknar vi enligt följande: fc = m × f/r fc = 10 × 2/1.5 fc =10 × 2,67 = 26,7 Newton. Så den totala spänningen är 98 + 26,7 = 124,7 Newton. 
Att dela upp gravitationen i två vektorer kan hjälpa dig att visualisera detta koncept bättre. När som helst i bågen av ett svängande föremåls rörelse bildar repet en vinkel på "θ" med linjen genom jämvikten och rotationens centrala punkt. När repet svänger kan du dela upp tyngdkraften (m × g) i 2 vektorer - mgsin(θ) är tangenten till bågen i jämviktsriktningen, och mgcos(θ), parallellen till spänningskraften i motsatt riktning. Spänningen behöver bara motverka mgcos(θ) - kraften som motverkar - inte hela tyngdkraften (förutom vid jämviktspunkten, när den är lika med spänningen). Antag att pendeln bildar en vinkel på 15 grader med vertikalen och sedan har en hastighet på 1,5 m/s. Vi hittar spänningen enligt följande: Stress på grund av gravitation (Tg) = 98cos(15) = 98(0,96) = 94,08 Newton centripetalkraft (Fc) = 10 × 1,5/1,5 = 10 × 1,5 = 15 Newton Total spänning = Tg + fc = 94,08 + 15 = 109,08 Newton. 
Antag att massan på 10 kg inte längre svänger utan dras med horisontellt på marken och på ett rep. Nu säger vi att marken har en kinetisk friktionskoefficient på 0,5 och att massan rör sig med konstant hastighet, men vi vill accelerera den med 1 m/s. Denna nya uppgift avslöjar två viktiga förändringar – den första är att vi inte längre behöver beräkna spänningen på grund av gravitationen, eftersom repet inte längre stödjer massan och motverkar kraften. Vi måste nu ta hänsyn till friktionskraften och den resulterande spänningen, såväl som spänningen som orsakas av objektets acceleration. Vi löser detta på följande sätt: Normalkraft (N) = 10 kg × 9.8 (acceleration genom gravitation) = 98 N Kinetisk friktionskraft (Fr) = 0.5 × 98 N = 49 Newton Accelerationskraften (Fa) = 10 kg × 1 m/s = 10 Newton Total spänning = Fr + fa = 49 + 10 = 59 Newton. 
Anta att vi har ett system med en massa på 10 kg (m1), ansluten vertikalt, via en remskiva, med en massa på 5 kg (m2) på en 60 graders lutning (vi antar att lutningen är friktionsfri). För att hitta spänningen i repet är det lättare att vara först med att formulera ekvationer för krafterna som accelererar massorna. Fortsätt enligt följande: Den hängande massan är tyngre och vi behöver inte ta hänsyn till friktion, så vi vet att det sker en acceleration nedåt. Men spänningen i repet drar upp massan, så vi beräknar nettokraften på repet enligt följande: F = m1(g) - T, eller 10(9.8) - T = 98 - T. Vi vet att massan kommer att accelerera uppför sluttningen. Eftersom sluttningen är friktionsfri vet vi att spänningen drar massan uppför sluttningen, endast hållen tillbaka av viktens egen massa. Kraftkomponenten som drar ner vikten beräknas med mgsin(θ), så i vårt fall kan vi säga att vikten uppför accelererar lutningen med nettokraften F = T - m2(g)sin(60) = T - 5(9.8)(.87) = T - 42.63. Accelerationen för de två massorna är densamma, så vi har (98 - T)/m1 = T - 42.63/m2. Efter lite enkel algebra får vi T = 61.09 Newton. 
Antag i detta Y-formade system att föremålet har en vikt på 10 kg och att de två översta repen bildar en vinkel med taket på 30 grader och 60 grader. Om vi vill hitta spänningen i vart och ett av de översta repen måste vi överväga de vertikala och horisontella komponenterna av spänningen för varje rep. De två repen i detta exempel hänger vinkelrätt mot varandra, vilket gör det enkelt att beräkna dessa spänningar, enligt definitionerna av de trigonometriska funktionerna. Så som följer: Förhållandet mellan T1 eller T2 och T = m(g) är lika med sinus för vinkeln mellan varje stödlina och taket. för T1 är sin(30) = 0,5, medan för T2 anser att sin(60) = 0,87. Multiplicera spänningen i bottenrepet (T = mg) med sinus för varje vinkel för att få T1 och t2 att hitta. t1 =0,5 × m(g) =0,5 × 10(9,8) = 49 Newton. t2 =0,87 × m(g) =0,87 × 10(9,8) = 85,26 Newton.
Beräkna krafter i fysik
Inom fysiken är spänning den kraft som ett rep, snöre, kabel eller liknande föremål utövar på ett eller flera andra föremål. Allt som dras är upphängt, stött eller fäst i ett rep.d. svänger, utsätts för spänningskraften. Liksom andra krafter kan spänningar accelerera eller deformera föremål. Att kunna beräkna spänning är en viktig färdighet för fysikstudenter, men också för ingenjörer och arkitekter. När allt kommer omkring, för att designa säkra byggnader måste de veta exakt om spänningen på en kabel tål belastningen av ett föremål. Fortsätt läsa i steg 1 för att lära dig hur du beräknar stress i olika fysiska system.
Steg
Metod 1 av 2: Bestämning av spänningen på en enda sladd

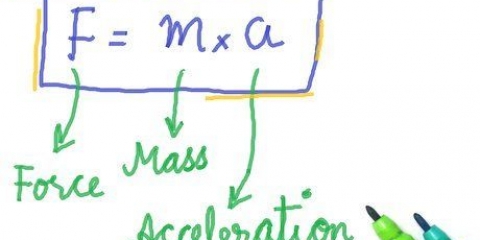
1. Bestäm krafterna på varje sida av tråden. Spänningen i en given tråd av ett rep är summan av alla krafter som drar repet från båda ändarna. Glöm inte: kraft = massa × acceleration. Anta att repet sträcks hårt, då kommer varje förändring i accelerationen eller massan av föremålen som repet stöder att orsaka en förändring i spänningen i repet. Glöm det konstanta acceleration på grund av gravitation inte heller – även när ett system är i vila, utsätts varje komponent för gravitationen. Spänningen i ett visst rep kan uttryckas som T = (m × g) + (m × a), där "g" accelerationen beror på tyngdkraften hos något föremål som stöds av repet, och "a" är varje annan acceleration på något föremål som stöds av repet.
- För enkelhetens skull kan vi anta att vi har att göra med enidealisk tråd – med andra ord att repet, kabeln osv. är tunn och masslös och kan inte sträcka sig eller gå sönder.
- Ett exempel: anta att vi har ett system där en massa hänger från en träbalk, fäst med ett enda rep (se bild). Fortfarande rör massorna fortfarande repet – hela systemet är i vila. Vi vet nu att massan är i jämvikt, där spänningskraften är lika med gravitationskraften på massan. Med andra ord, spänning (Ft) = Kraft eller gravitation (Fg) = m × g.
- Anta att vi har en massa på 10 kg, då gäller följande: spänning = 10 kg × 9,8 m/s = 98 Newton.

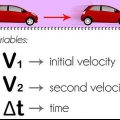
2. Var uppmärksam på accelerationen. Tyngdkraften är inte den enda kraften som påverkar spänningen i ett rep - vilken kraft som helst kan associeras med accelerationen av ett föremål som repet är kopplat till. Om ett hängande föremål accelereras av en kraft på repet eller kabeln, adderas kraften som orsakas av accelerationen (massa × acceleration) till spänningen som orsakas av föremålets massa.

3. Ta också hänsyn till en cirkulär växel. Ett föremål som roteras runt en central punkt på ett rep (som en pendel) utövar en spänning på repet som orsakas av centripetalkraften. Centripetalkraft är den kraft som repet utövar på ett föremål genom att dra det inåt "Dra", så att föremålet fortsätter att röra sig i en båge, istället för att gå rakt. Ju snabbare föremålet rör sig, desto större centripetalkraft. centripetalkraft (Fc) är lika med m × v/r där "m" är lika med massan, "v" är hastigheten och "r" är cirkelns radie, det vill säga den bana som objektet rör sig i.

4. Förstå att spänningen på grund av gravitationen förändras under pendelns period. Som nämnts tidigare ändras både riktningen och storleken på centripetalkraften när ett föremål svänger. Men även om gravitationen förblir konstant spänning på grund av gravitationen också ändra. Som ett svängande föremål inte botten av pendelsvängningen (jämviktspunkten), sedan drar tyngdkraften rakt ner, men spänningen drar i föremålet i en vinkel. På grund av detta kommer spänningen att ta bort en del av gravitationskraften, men inte helt.

5. Tänk också på friktionen. Varje föremål som dras genom ett rep och som upplever friktion från ett annat föremål (eller vätska) överför denna friktionskraft till spänningen i repet. Friktionskraften mellan två föremål beräknas på samma sätt som i alla andra situationer – med följande ekvation: Kraft genom friktion Fr = (mu)N, där mu är friktionskoefficienten mellan de två föremålen och där N är normalkraften mellan de två föremålen (kraften med vilken de trycker mot varandra). Observera att statisk friktion – friktionen som uppstår när du försöker flytta ett stillastående föremål – skiljer sig från kinetisk friktion – den friktion som uppstår när du försöker hålla ett rörligt föremål i rörelse.
Metod 2 av 2: Beräkna spänning på flera ackord

1. Lyfta parallella vertikala laster med en remskiva. En remskiva är en enkel maskin som består av ett upphängt hjul som låter spänningskraften i ett rep ändra riktning. I en enkel installation löper repet eller kabeln från en hängande massa upp genom remskivan, sedan ner till en annan massa, vilket ger dig två längder rep. Men spänningen i båda delarna av repet är densamma, även om massor av olika storlekar hänger från båda ändarna av repet. I ett system med två massor upphängda i en remskiva är spänningen lika med 2g(m1)(m2)/(m2+m1), varvid "g" accelerationen beror på gravitationen, "m1" massan av objekt 1 och "m2" massan av föremål 2. Observera att eftersom en massa är tyngre än den andra, kommer systemet att accelerera, med 10 kg som rör sig ner och 5 kg uppåt.
- Observera att vi antar en "idealisk remskiva – ingen massa, ingen friktion och remskivor som inte kan gå sönder, deformeras eller lossna från taket.
- Anta att vi har två massor hängande från en remskiva, på parallella rep. Vikt 1 har en massa på 10 kg och vikt 2 har en massa på 5 kg. I det här fallet hittar vi spänningen enligt följande:
- T = 2g(m1)(m2)/(m2+m1)
- T = 2(9,8)(10)(5)/(5 + 10)
- T = 19,6(50)/(15)
- T = 980/15
- T = 65,33 Newton.
2. Lyftvikter med en remskiva på linor som är vertikala men inte parallella. Remskivor används ofta för att få spänning i en annan riktning än upp eller ner. Till exempel, om en massa hänger vertikalt från ena änden av repet, medan en andra massa är bunden på en sluttning i den andra änden, kommer detta icke-parallella remskivasystem att ha formen av en triangel vars hörn är den första massan, den andra massan och själva remskivan. I detta fall bestäms spänningen i repet av både tyngdkraften på massan och av komponenten av dragkraften som verkar parallellt med den diagonala delen av repet.

3. Använda flera sladdar för att hänga ett föremål. Slutligen överväger vi fallet där ett föremål hänger på en "Y-formad" system av rep – två rep är fästa i taket och möts vid en central punkt, där en vikt hänger från ett tredje rep. Spänningen i det tredje repet är uppenbar – detta är helt enkelt den resulterande spänningen på grund av gravitationen. Spänningarna i de andra två repen är olika och, när de läggs ihop, bör de vara lika med gravitationen i en uppåtgående och vertikal riktning, och lika med noll i en horisontell riktning (förutsatt att systemet är i vila). Spänningen i repen påverkas av massan på det hängande föremålet samt vinkeln för varje rep mot taket.
"Beräkna krafter i fysik"
Оцените, пожалуйста статью