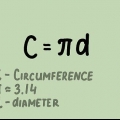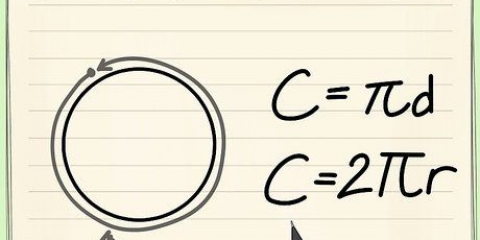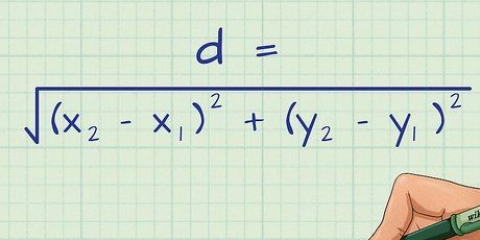Lägg en tråd runt omkretsen, så exakt som möjligt. Markera tråden när cirkeln är klar, mät sedan längden på tråden med en linjal. 




π=3 + 4/(2*3*4) - 4/(4*5*6) + 4/(6*7*8) - 4/(8*9*10) + 4/(10*11) *12) - 4/(12*13*14) ... Du tillämpar denna formel genom att först ta 2 och sedan växelvis addera och subtrahera bråk, med täljaren 4 och nämnaren produkten av 3 på varandra följande heltal som ökar med varje ny iteration. Varje på varandra följande bråkdel börjar med en serie heltal där det första talet i serien är det sista talet i den föregående serien (i det föregående bråket). Även om du bara gör detta ett fåtal gånger kommer du snart nära pi. 


pi=2 *(Arcsin(sqrt(1 - x^2))) + abs(Arcsin(x)). Arcsin hänvisar till en invers sinus i radianer Sqrt är en förkortning för kvadratroten av Abs är en förkortning för absolut värde x^2 är en viss potens, i detta fall x i kvadrat.
Beräkna pi
Pi (π) är ett av de viktigaste och mest fascinerande talen i matematik. Visas helt enkelt som 3.14, används som en konstant för att beräkna omkretsen av en cirkel, med hjälp av dess radie eller diameter. Det är också ett irrationellt tal, vilket betyder att du kan beräkna det till ett oändligt antal decimaler utan att någonsin stöta på ett upprepande mönster. Detta gör det svårt, men inte omöjligt, att arbeta exakt.
Steg
Metod 1 av 5: Beräkna Pi med hjälp av en cirkel

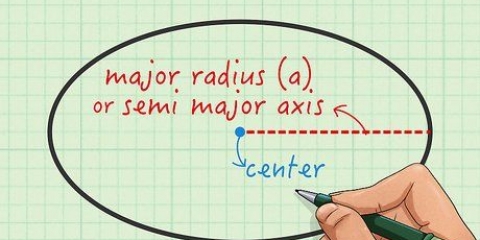
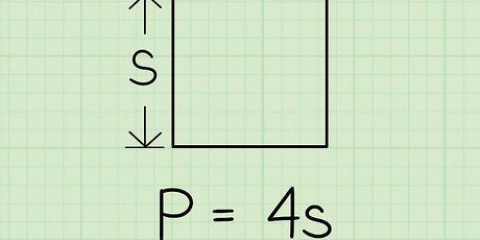
1. Se till att använda en perfekt cirkel. Den här metoden fungerar inte med en ellips, ellips eller något annat än en riktig cirkel. En cirkel definieras som alla punkter i ett plan som är lika långt från en given centralpunkt. Till exempel är lock på en syltburk ett trevligt redskap att använda för denna övning. Du kan grovt räkna ut ett värde på Pi med detta. Även den tunnaste, vassaste pennan är fortfarande enorm jämfört med den noggrannhet som krävs för en exakt beräkning av talet Pi.

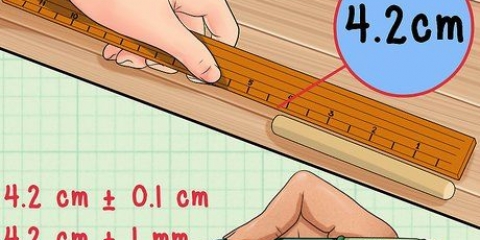
2. Mät cirkelns omkrets så noggrant du kan. Omkretsen är längden på hela cirkelns omkrets. Eftersom det här går runt kan det vara lite knepigt att mäta (det är därför Pi är så viktigt).

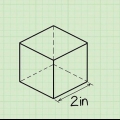
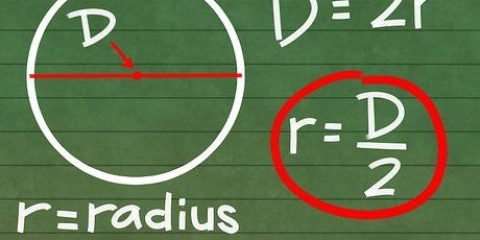
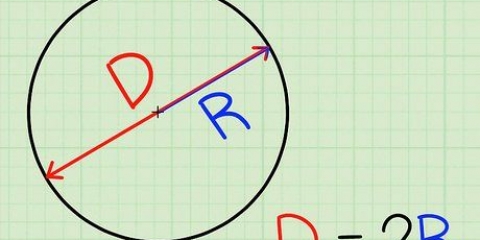
3. Mät diametern på cirkeln. Diametern är längden av en cirkels tvärsnitt genom cirkelns mitt.

4. Använd formeln. Omkretsen av en cirkel kan hittas med formeln C=π*d=2*π*r. Så pi är lika med cirkelns omkrets dividerat med diametern. Skriv in dina siffror i en miniräknare: resultatet bör vara cirka 3.ska vara 14.

5. För ett mer exakt resultat, upprepa denna process i flera cirklar och sedan genomsnittet av resultaten. Dina avläsningar kanske inte är perfekta när det kommer till en individuell läsning, men med tiden bör genomsnittet vara en riktigt bra uppskattning av Pi.
Metod 2 av 5: Beräkna Pi med hjälp av Infinite Series

1. Använd Gregory-Leibniz-serien. Matematiker har hittat flera matematiska sekvenser som, om de följs till oändligheten, kan beräkna Pi till ett enormt antal decimaler. Vissa av dessa sekvenser är så komplexa att det krävs superdatorer för att bearbeta dem. En av de enklaste är dock Gregory-Leibniz-serien. Kanske inte särskilt effektivt, men det ger ett mer exakt tal för pi med varje iteration, och slutar så småningom på 5 decimaler efter 500.000 iterationer. Här är formeln att använda.
- π=(4/1) - (4/3) + (4/5) - (4/7) + (4/9) - (4/11) + (4/13) - (4/15) ...
- Ta 4 och subtrahera 4 dividerat med 3 från detta. Lägg sedan till 4 dividerat med 5. Subtrahera sedan 4 dividerat med 7 igen. Fortsätt att upprepa detta mönster med en täljare 4 och ett på varandra följande udda tal i nämnaren. Ju mer du gör detta, desto närmare pi kommer du.

2. Dra nytta av Nilakantha-serierna. Detta är en annan oändlig serie som låter dig beräkna pi och är inte svår att förstå. Även om det är lite mer komplicerat, kan du beräkna pi mycket snabbare med den än med Leibniz-formeln.
Metod 3 av 5: Beräkna Pi med Buffons nålproblem

1. Prova följande experiment för att beräkna pi genom att kasta korv. Pi ingår också i tankeexperimentet som kallas Buffons nålproblem, som försöker bestämma sannolikheten för att slumpmässigt kastade föremål med liknande form kommer att landa mellan eller på en serie parallella linjer på golvet. Det visar sig att om avståndet mellan linjerna är lika med längden på de kastade föremålen, så kan antalet gånger föremålen landar på en linje efter många kast användas för att beräkna pi.
- Forskare och matematiker har ännu inte upptäckt ett sätt att beräkna pi exakt, eftersom de ännu inte har hittat ett material så tunt att man kan utföra exakta beräkningar med det.
Metod 4 av 5: Beräkna Pi med en gräns

1. Välj ett stort antal. Ju större siffra, desto mer exakt blir din beräkning.

2. Använd talet, som vi kallar x, i denna formel för att beräkna pi:x *sin (180 / x). För att detta ska fungera, se till att din miniräknare är inställd på grader. Anledningen till att detta kallas en limit är att dess resultat är "begränsat" till pi. När du ökar ditt nummer x kommer resultatet närmare och närmare värdet på pi.
Metod 5 av 5: Arcsinus och invers sinusfunktion
1. Välj ett tal mellan -1 och 1. Detta beror på att arcsine inte är definierad för tal större än 1 eller mindre än -1.
2. Använd talet i följande formel och resultatet är ungefär lika med pi.
Tips
- Att beräkna pi är roligt och utmanande, men om du beräknar för många decimaler kommer det inte att vara till stor nytta .Astronomer säger att det inte krävs mer än 39 decimaler för talet pi att göra mycket exakta beräkningar.
Оцените, пожалуйста статью