Om det experimentella måttet är 60 cm, måste beräkningen av felaktigheten också avrundas till ett heltal. Till exempel kan felaktigheten i denna mätning vara 60 cm ± 2 cm, men inte 60 cm ± 2.2 cm. Om din experimentella läsning är lika med 3.4 cm, då måste även felaktigheten avrundas till 0,1 cm. Till exempel kan felaktigheten i denna mätning vara 3.4 cm ± .vara 1 cm, men inte 3.4 cm ± 1 cm. 
Titta noga på kanten av bollen och linjalen för att få en uppfattning om hur tillförlitlig din mätning kan vara. I en standardlinjal är 0,5 cm-märkena tydligt markerade – men anta att du kan komma lite närmare än så. Om det ser ut som att du kan komma inom 0,3 cm med ditt mått, så är felaktigheten 0,3 cm. Nu ska vi mäta bollens diameter. Anta att du får 7,6 cm som svar. Skriv nu ner det uppskattade måttet med felaktigheten. Kulans diameter är 7,6 cm ± 0,3 cm. 
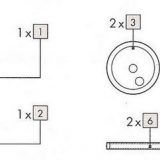
Anta att du inte kan komma mycket närmare än 0,2 cm med en vanlig linjal. Så, felaktigheten är ± 0,2 cm. Anta att du mätte att stapeln med lådor tillsammans är 22 cm. Nu behöver du bara dividera detta mätvärde och felaktigheten med 10 (antalet rutor). 22 cm/10 = 2,2 cm och 0,2 cm/10 = 0,02 cm. Detta betyder att tjockleken på 1 låda är lika med 2,20 cm ± 0,02 cm. 



0,43 s – 0,42 s = 0,01 s 0,52s - 0,42s = 0,1s 0,35 s - 0,42 s = -0,07 s 0,29 s - 0,42 s = -0,13 s 0,49 s - 0,42 s = 0,07 s Lägg nu till kvadraterna av skillnaderna: (0,01 s) + (0,1 s) + (-0,07 s) + (-0,13 s) +(0,07 s)= 0,037 s. Hitta medelvärdet av dessa tillagda kvadrater genom att dividera resultatet med 5. 0,037 s/5 = 0,0074 s. 



(10 cm ± .4 cm) - (3 cm ± .2 cm) = (10 cm - 3 cm) ± (.4 cm +. 2 cm) = 7 cm ± 0,6 cm (6 cm ± 0,2 cm) = (0,2 / 6) x 100 och lägg till ett %-tecken till det. Det är 3,3 %
Således:
(6 cm ± 0,2 cm) x (4 cm ± 0,3 cm) = (6 cm ± 3,3 %) x (4 cm ± 7,5 %) (6 cm x 4 cm) ± (3.3 + 7,5) = 24 cm ± 10,8 % = 24 cm ± 2,6 cm (10 cm ± 0,6 cm) ÷ (5 cm ± 0,2 cm) = (10 cm ± 6%) ÷ (5 cm ± 4%) (10 cm ÷ 5 cm) ± (6% + 4%) = 2 cm ± 10 % = 2 cm ± 0,2 cm 
(2,0 cm ± 1.0 cm) = (2,0 cm) ± (1,0 cm) x 3 = 8,0 cm ± 3 cm
Beräkna felaktighet
När du gör en mätning medan du samlar in data kan du anta att det finns en "riktigt värde" ligger inom intervallet för de mätningar du har gjort. Om du vill beräkna felaktigheten i dina avläsningar måste du hitta den bästa uppskattningen av din avläsning och ta hänsyn till det när du subtraherar eller lägger till felaktigheten i avläsningen.
Steg
Metod 1 av 3: Lär dig grunderna

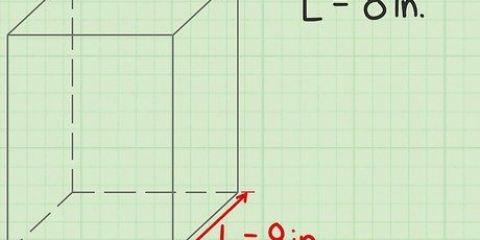
1. Bestäm rätt form för felaktighet. Anta att du mäter längden på en pinne på cirka 4,2 cm, med en marginal på 1 millimeter. Det betyder att pinnen nästan säkert är 4,2 cm, men kan vara något större eller mindre än denna längd, med en felmarginal på 1 millimeter.
- Anteckna detta enligt följande: 4,2 cm ± 0,1 cm. Du kan skriva om detta som: 4,2 cm ± 1 mm, eftersom 0,1 cm = 1 mm.

2. Avrunda den experimentella avläsningen till samma antal decimaler som felaktigheten. Mätningar som involverar felaktigheter avrundas vanligtvis till 1 eller 2 signifikanta siffror. Nyckelpunkten är att du avrundar experimentets mätningar till samma antal decimaler som felaktigheten, för att hålla måtten konsekventa.

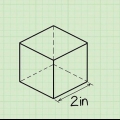
3. Beräkna felaktigheten för en enda mätning. Anta att du mäter diametern på en rund boll med en linjal. Detta är knepigt eftersom det är svårt att precisera var bollens ytterkant är och hur man mäter den med linjalen. Anta att linjalen kan hitta diametern med en noggrannhet på 0,1 cm - det betyder inte att du kan mäta bollens diameter till den precisionsnivån.

4. Beräkna felaktigheten för en enda mätning av flera objekt. Anta att du mäter höjden på en stapel med 10 CD-fodral som alla har dimensioner. Anta att du vill veta vad tjockleken på en låda är. Denna läsning är så liten att andelen felaktigheter kommer att vara överkant. Men om du mäter 10 lådor kan du dela resultatet och bara dividera dess felaktighet med antalet lådor i högen för att hitta tjockleken på 1 låda.

5. Utför denna mätning flera gånger. För att öka noggrannheten i din mätning, oavsett om du mäter längden på ett objekt eller hur lång tid det tog att resa en viss sträcka, ökar du chansen för en exakt mätning om du gör flera mätningar. Att bestämma medelvärdet av alla mätningar kommer i slutändan att resultera i en bättre bestämning av felaktigheten i en mätning.
Metod 2 av 3: Beräknar felaktigheten i flera mätningar

1. Ta flera mätningar. Anta att du vill beräkna hur lång tid det tar för en boll att falla från bordet till rundan. För bästa resultat måste du utföra samma mätning minst ett par gånger – låt oss säga att vi gör det fem gånger. Sedan måste du beräkna medelvärdet av dessa 5 mätningar och sedan addera eller subtrahera standardavvikelsen från detta, för bästa resultat.
- Anta att du har följande avläsningar: 0,43 s, 0,52 s, 0,35 s, 0,29 s och 0,49 s.

2. Bestäm medelvärdet av mätningarna. Det gör du genom att lägga ihop alla fem och dividera summan med 5, antalet uppmätta värden. 0,43 s + 0,52 s + 0,35 s + 0,29 s + 0,49 s = 2.08 s. Dela nu 2.08 av 5. 2.08/5 = 0,42 sek. Medelvärdet är 0,42 s.

3. Bestäm variansen för dessa mätningar. Det gör du genom att bestämma skillnaden mellan var och en av de 5 mätningarna och medelvärdet. Subtrahera avläsningarna från 0,42 s. Här är de 5 skillnaderna:

4. Bestäm standardavvikelsen. Detta kan hittas genom att beräkna kvadratroten av variansen. Kvadraten på 0,0074 s = 0,09 s, så standardavvikelsen är 0,09 s.

5. Ange det slutliga uppmätta värdet. Detta gör du genom att notera medelvärdet av de uppmätta värdena tillsammans med den adderade och subtraherade standardavvikelsen. Eftersom medelvärdet av avläsningarna är 0,42 s och standardavvikelsen är 0,09 s, är slutavläsningen 0,42 s ± 0,09 s.
Metod 3 av 3: Aritmetiska operationer med inexakthet

1. Lägger till felaktigheter. Du gör detta genom att lägga till avläsningarna och lägga till deras felaktigheter:
- (5 cm ± .2 cm) + (3 cm ± .1 cm) =
- (5cm + 3cm) ± (.2 cm +. 1 cm) =
- 8 cm ± .3 cm

2. Att subtrahera felaktigheter. Du gör detta genom att subtrahera de uppmätta värdena och lägga till felaktigheterna:
3. Multiplicerad felaktighet.
För att multiplicera onoggrannhet, multiplicera måtten och addera den RELATIVA felaktigheten (i procent):
Att beräkna felaktigheter genom multiplikation fungerar inte med absoluta värden (som med addition och subtraktion), men det gör det med relativa värden. Du får den relativa felaktigheten genom att dividera den absoluta felaktigheten med det uppmätta värdet och sedan multiplicera det med 100.
Till exempel:
För att multiplicera onoggrannhet, multiplicera måtten och addera den RELATIVA felaktigheten (i procent):
Att beräkna felaktigheter genom multiplikation fungerar inte med absoluta värden (som med addition och subtraktion), men det gör det med relativa värden. Du får den relativa felaktigheten genom att dividera den absoluta felaktigheten med det uppmätta värdet och sedan multiplicera det med 100.
Till exempel:
Således:
4. Delar felaktigheter.
För att dela in noggrannhet, dela måtten och lägg till den RELATIVA felaktigheten:
Denna procedur motsvarar en multiplikation!
För att dela in noggrannhet, dela måtten och lägg till den RELATIVA felaktigheten:
Denna procedur motsvarar en multiplikation!

5. Ökar en felaktig läsning exponentiellt. För att exponentiellt öka en felaktig mätning, öka mätningen med en viss potens och multiplicera sedan felaktigheten med den potensen:
Tips
- Du kan visa resultaten och standardinexaktheten som helhet eller för varje resultat inom en uppsättning data. En generell regel är att data som erhålls från flera mätningar är mindre exakta än direkt erhållna från en enskild mätning.
Varningar
- Inexakthet som beskrivs här är endast tillämplig i de fall där normal (gaussisk, klockformad) statistik används. Andra uppslag kräver en annan metod för att beskriva felaktigheter.
- Bra forskning tar aldrig slut "fakta" eller vad "Sann" är. Även om en mätning med stor sannolikhet faller inom ett visst intervall av inexakthet, finns det ingen garanti för att den kommer att göra det. Det är inneboende i vetenskapliga mätvärden att det finns en möjlighet att mätvärden är felaktiga.
Оцените, пожалуйста статью