Inom ett batteri sker kemiska reaktioner som producerar en ansamling av elektroner. Elektronerna går till den negativa änden, medan den positiva änden förblir mestadels tom (dessa kallas de negativa och positiva polerna). Ju längre detta pågår, desto större kommer spänningen mellan de två att öka. När du kopplar en tråd mellan den negativa och positiva änden kan elektronerna på den negativa änden plötsligt gå någonstans. De skjuter mot det positiva slutet och skapar en ström. Ju högre spänning, desto fler elektroner kommer att flyttas till den positiva änden per sekund. 
Ett motstånd är allt i en krets som adderar motstånd. Du kan köpa ett riktigt "motstånd" i en elektronikaffär, men i ett kretsschema representeras detta ofta av ett ljus eller något annat med resistans. 
Ström=spänning dividerat med resistans Detta noteras vanligtvis enligt följande: I = /R Tänk på vad som händer när du ökar V (spänning) eller R (motstånd). Stämmer detta med vad du lärde dig i förklaringen ovan? 

Till exempel: de tre motstånden R1, R2 och R3 respektive har ett motstånd på 2 Ω (ohm), 3 Ω och 5. Det totala motståndet är 2 + 3 + 5 = 10 ohm. 
Ohms lag säger att strömmen I = /R. Spänningen över hela kretsen är 12 volt och det totala motståndet är 10 ohm. Svaret är jag =/10 = 1,2 ampere. 
jag =/R IR = R/R IR = V V = IR 
Spänning över R1 = V1 = (1,2A)(2Ω)=2,4 volt. Spänning över R2=V2=(1,2A)(3Ω)=3,6 volt. Spänning över R3=V3=(1,2A)(5Ω)=6,0 volt. 
I vårt exempel: 2,4 + 3,6 + 6,0 = 12 volt; spänningen över hela kretsen. Om ditt svar är något avvikande (t.ex. 11,97 istället för 12), avrundade du förmodligen en siffra någon gång. Svaret är fortfarande korrekt. Kom ihåg att spänningen indikerar skillnaden i laddning (eller antalet elektroner). Föreställ dig att räkna antalet nya elektroner du ser när du färdas längs kretsen. Om du räknar detta rätt kommer du att få den totala förändringen av elektroner från början till slutet. 


Kom ihåg att addering av spänningsfall i en seriekrets alltid resulterar i den totala spänningen över kretsen. Tänk på vilken väg som helst som strömmen följer i en seriekrets. Samma sak gäller detta: om du lägger ihop alla spänningsfall kommer du att hamna på den totala spänningen. Eftersom strömmen inte går genom mer än ett motstånd genom var och en av de två ledningarna, måste spänningen över dessa motstånd vara lika med den totala spänningen. 
I matematiska termer: Itotal=Jag1 + jag2 + jag3... Om du har svårt att förstå detta, föreställ dig en bong som delar sig i två banor. Det totala vattenflödet är helt enkelt mängden vatten som strömmar genom varje rör lagt samman. 
/Rtotal =/R1 + /R2 + /R3 ... Till exempel har en krets ett motstånd på 2 ohm och 4 ohm, parallellt. /Rtotal=1/2 + 1/4 = 3/4 → 1 =
Beräknar spänningen över ett motstånd
Innan du kan beräkna spänningen över ett motstånd måste du först bestämma vilken typ av krets du har att göra med. Om du vill ha en översikt över grunderna eller lite hjälp med att förstå kretsar, börja med det första avsnittet. Om detta är något för dig, hoppa över den här delen och gå vidare till den typ av krets du vill lösa.
Steg
Del 1 av 3: Förstå kretsar

1. Förstå flödet. Låt oss tänka på makt med en analogi: Anta att du häller en påse majs i en skål. Varje korn av majs är en elektron, och flödet av korn är den elektriska strömmen. När vi talar om ett flöde beskriver vi det genom att säga hur många korn per sekund som passerar en viss punkt. När vi pratar om en elektrisk ström mäter vi in den ampere (A), eller ett visst (mycket stort) antal elektroner som strömmar förbi en viss punkt per sekund.

2. Förstå elektrisk laddning. Elektroner har en "negativ" elektrisk laddning. Det betyder att de attraherar (eller flyter i den riktningen) objekt med en positiv laddning, och stöter bort (eller flyter bort) objekt med en negativ laddning. Eftersom de alla är negativa försöker elektroner alltid hålla sig borta från andra elektroner och spridas där det är möjligt.

3. Förstå spänning. Spänning mäter skillnaden i elektrisk laddning mellan två punkter. Ju större skillnaden är, desto mer attraherar de två sidorna varandra. Här är ett exempel med ett vanligt batteri:

4. Bestäm motståndet. Motstånd är precis vad det låter som. Ju mer motstånd något har, desto svårare är det för elektronerna att passera. Detta saktar ner strömmen, eftersom färre elektroner kan flyttas per sekund.

5. Memorera Ohms lag. Det finns ett mycket enkelt samband mellan ström, spänning och resistans. Skriv ner detta eller kom ihåg formeln; du använder det ofta när du felsöker kretsproblem:
Del 2 av 3: Beräkna spänningen över ett motstånd (seriekoppling)

1. Förstå en seriekrets. En seriekrets är lätt att känna igen. Det är bara en trådslinga med allt ordnat i rad. Ström flyter genom hela slingan, och varje motstånd eller element i sekvens.
- De nuvarande är alltid densamma vid varje punkt i kretsen.
- Vid beräkning av spänningen spelar det ingen roll var motståndet sitter i kretsen. Du kan flytta motstånden utan att ändra spänningen över varje motstånd.
- Vi kommer att använda en exempelkrets med tre motstånd i serie: R1, R2 och R3. Den drivs av ett 12 volts batteri. Vi kommer att bestämma spänningen över var och en.

2. Beräkna det totala motståndet. Lägg ihop alla värden för motstånden i kretsen. Summan är det totala motståndet för seriekretsen.

3. Bestäm strömmen. Använd Ohms lag för att bestämma strömmen för hela kretsen. Kom ihåg att strömmen är densamma i hela seriekretsen. När vi väl beräknat strömmen på detta sätt kan vi använda den för alla våra beräkningar.

4. Justera Ohms lag för spänning. Med någon grundläggande algebra kan vi modifiera Ohms lag så att vi löser för spänning istället för ström med den:

5. Beräkna spänningen över varje motstånd. Vi känner till motståndet, vi känner till strömmen och vi har vår ekvation. Byt ut värdena och lös ekvationen. Här är vårt exempelproblem löst för alla tre motstånd:

6. Kontrollera ditt svar. I en seriekrets måste summan av alla dina svar vara lika med den totala spänningen. Lägg ihop varje spänning som du har beräknat och kontrollera om denna är lika med spänningen över hela kretsen. Om inte, gå tillbaka och kontrollera ditt arbete för fel.
Del 3 av 3: Beräkna spänningen över ett motstånd (parallell krets)

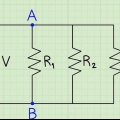
1. Förstå parallellkretsen. Föreställ dig en ledning som lämnar ena änden av ett batteri och sedan delas i två separata ledningar. Dessa två kablar löper parallellt med varandra och kommer sedan samman igen innan de når den andra änden av batteriet. Om det finns ett motstånd över den vänstra ledningen och ett motstånd över den högra ledningen, är dessa två motstånd anslutna "parallellt".
- Valfritt antal ledningar kan delas av från en parallellkrets. Dessa egenskaper kommer fortfarande att gälla för en krets som delas i hundra ledningar som sedan sammanfogas igen.

2. Tänk på hur flödet rör sig. Ström i en parallellkrets kommer att röra sig längs vilken tillgänglig väg som helst. Elektrisk ström kommer att passera genom ledningen till vänster, korsar det vänstra motståndet och når den andra änden. Samtidigt kommer strömmen att passera genom ledningen till höger, korsa det högra motståndet och sedan nå slutet. Ingen del av strömmen kommer att vända eller flyta genom två parallella motstånd.

3. Med hjälp av den totala spänningen kan du hitta spänningen över varje motstånd. Om du känner till spänningen över hela kretsen är svaret förvånansvärt enkelt. Varje parallelltråd har samma spänning som hela kretsen. Antag att en krets med två parallella motstånd drivs av ett 6 volts batteri. Spänningen över resistorn på det vänstra motståndet är 6 volt och spänningen över det högra motståndet är 6 volt. Det spelar inte ens roll hur mycket motstånd det finns. För att förstå varför, tänk tillbaka på seriekretsarna som beskrivs ovan:

4. Beräkna den totala strömmen i kretsen. Om problemet inte talar om för dig den totala spänningen över kretsen, måste du ta några extra steg. Börja med att bestämma den totala strömmen genom kretsen. I en parallellkrets är den totala strömmen lika med summan av den elektriska strömmen genom varje parallell bana.

5. Beräkna det totala motståndet i kretsen. Motstånd är mindre effektiva i en parallellkrets eftersom de bara blockerar strömmen som flyter genom en viss tråd. Faktum är att ju fler ledningar det finns, desto lättare är det för strömmen att hitta ett sätt. För att beräkna det totala motståndet, lös för Rtotal i denna ekvation:
(3/4)Rtotal → Rtotal=1/(3/4) = 4/3=~1,33 ohm.
- En krets har en ström på 5 ampere som flyter genom den. Det totala motståndet är 1,33 Ohm.
- Enligt Ohms lag: I = V / R, så V = IR
- V = (5A)(1,33Ω)=6,65 volt.

1. Bestäm spänningen från dina svar. Kom ihåg att när vi väl hittar den totala spänningen över kretsen vet vi spänningen över en av de parallella ledningarna. Lös problemet för hela kretsen med Ohms lag. Här är ett exempel:
Tips
- Har du att göra med en komplicerad krets med motstånd i serie och parallella motstånd, välj två närliggande motstånd. Bestäm vid behov det totala motståndet över dessa motstånd med hjälp av reglerna för parallell- eller seriemotstånd. Nu kan du närma dig dem som ett motstånd. Fortsätt göra detta tills du har en enkel krets med eller parallell motstånd eller seriekopplade motstånd.
- Spänningen över ett motstånd kallas ofta för ett "spänningsfall".
- Lär dig terminologin:
- Kretsar - sammansatt av element (motstånd, kondensatorer och induktorer) anslutna med ledningar genom vilka en elektrisk ström kan passera.
- Motstånd - element som kan minska eller motverka elektrisk ström.
- Amperage - laddningsflödet i ledningar; enhet: ampere, A
- Spänning - arbete per laddningsenhet; enhet; spänning: V
- Motstånd - graden till vilken ett element motstår elektrisk ström; enhet: ohm,
"Beräknar spänningen över ett motstånd"
Оцените, пожалуйста статью