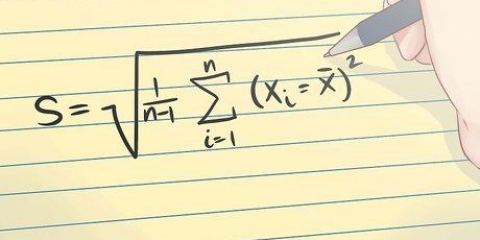I datainsamlingsexemplet blir dessa avvikelser: 







För att kontrollera giltigheten av dina beräkningar kontrollerar vi om summan av värdena i kolumnen med avvikelser är lika med noll. Lägger du ihop alla avvikelser och du får något annat än noll så är ditt medelvärde felaktigt eller så har du gjort ett fel i beräkningen av en eller flera av avvikelserna. Återvänd och kontrollera ditt arbete. 
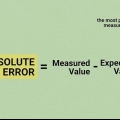
Absolutvärde är ett matematiskt verktyg för att indikera avstånd eller magnitud, oavsett riktning. För att bestämma det absoluta värdet, utelämna helt enkelt minustecknet för varje nummer i den andra kolumnen. Så fyll den tredje kolumnen med de absoluta värdena enligt följande: 









För denna datauppsättning blir den slutliga beräkningen: 

Till exempel, med denna datamängd kan du säga att medelvärdet är nio och medelavståndet från medelvärdet är 2,75. Observera att vissa värden är närmare än 2,75 jämfört med andra. Men 2,75 är medeldistansen.
Beräknar medelavvikelsen från medelvärdet
När du arbetar med data finns det flera sätt att mäta hur snävt dina datavärden är grupperade. Det vanligaste är genomsnittet. De flesta lär sig att beräkna medelvärdet tidigt i skolan genom att hitta summan av en grupp datavärden och sedan dividera med antalet värden i gruppen. En mer avancerad beräkning är medelavvikelsen över medelvärdet. Denna beräkning talar om för dig hur nära dina värden är medelvärdet. Du bestämmer detta genom att hitta medelvärdet för en datamängd, sedan avvikelsen för varje data från det medelvärdet och sedan medelvärdet av dessa avvikelser.
Steg
Del 1 av 2: Beräkna medelvärdet

1. Samla in och räkna dina data. För varje uppsättning värden är medelvärdet ett mått på det centrala värdet. Beroende på typen av data kommer genomsnittet att ge dig mittvärdet av denna data. För att hitta medelvärdet måste du först samla in din data, antingen genom ett experiment eller bara ges det på en uppgift.
- Som exempel använder vi en given nummerföljd 6, 7, 10, 12, 13, 4, 8 och 12. Denna sekvens är tillräckligt liten för att räkna för hand, och snabbt se att det är en sekvens med åtta siffror.
- Inom statistiken, variabeln
eller
används ofta för att ange antalet värden i en serie eller samling.

2. Hitta summan av värdena. Det första steget för att bestämma medelvärdet är att beräkna summan av alla värden. Inom statistisk notation representeras i allmänhet varje värde av variabeln  . Summan av alla värden ges symbolen
. Summan av alla värden ges symbolen  . Den grekiska versalen sigma indikerar att det är summan av värdena. Beräkningen för denna enkla serie går så här:
. Den grekiska versalen sigma indikerar att det är summan av värdena. Beräkningen för denna enkla serie går så här:
 . Summan av alla värden ges symbolen
. Summan av alla värden ges symbolen  . Den grekiska versalen sigma indikerar att det är summan av värdena. Beräkningen för denna enkla serie går så här:
. Den grekiska versalen sigma indikerar att det är summan av värdena. Beräkningen för denna enkla serie går så här:

3. Dela för att hitta genomsnittet. Dela slutligen summan med antalet värden. Den grekiska bokstaven mu,  , används ofta för att ange medelvärdet. Beräkningen av genomsnittet går därför till enligt följande:
, används ofta för att ange medelvärdet. Beräkningen av genomsnittet går därför till enligt följande:
 , används ofta för att ange medelvärdet. Beräkningen av genomsnittet går därför till enligt följande:
, används ofta för att ange medelvärdet. Beräkningen av genomsnittet går därför till enligt följande:
Del 2 av 2: Fastställande av den genomsnittliga avvikelsen

1. Skapa en tabell. För att hålla din data i god ordning och för att hjälpa till med beräkningarna är det användbart att skapa en tabell med tre kolumner. Märk den första kolumnen  . Märk den andra kolumnen
. Märk den andra kolumnen  . Märk den tredje kolumnen
. Märk den tredje kolumnen  .
.
 . Märk den andra kolumnen
. Märk den andra kolumnen  . Märk den tredje kolumnen
. Märk den tredje kolumnen  .
. - Fyll den första kolumnen med värdena för din beräkning.

2. Beräkna avvikelsen (avvikelsen) för varje värde. I den andra kolumnen, märkt  , sätt avvikelsen eller skillnaden mellan varje värde och medelvärdet av serien eller mängden. Hitta detta värde genom att subtrahera medelvärdet från varje datavärde.
, sätt avvikelsen eller skillnaden mellan varje värde och medelvärdet av serien eller mängden. Hitta detta värde genom att subtrahera medelvärdet från varje datavärde.
 , sätt avvikelsen eller skillnaden mellan varje värde och medelvärdet av serien eller mängden. Hitta detta värde genom att subtrahera medelvärdet från varje datavärde.
, sätt avvikelsen eller skillnaden mellan varje värde och medelvärdet av serien eller mängden. Hitta detta värde genom att subtrahera medelvärdet från varje datavärde.








3. Bestäm det absoluta värdet för varje avvikelse. När du beräknar avvikelsen för något värde från medelvärdet vill du bara veta skillnaden, inte om den skillnaden är positiv eller negativ. Vad du verkligen behöver, i matematiska termer, är det absoluta värdet av skillnaden. Det absoluta värdet indikeras med vertikala streck| |.










4. Beräkna medelvärdet av de absoluta avvikelserna. Efter att ha slutfört tabellen med tre kolumner, hitta medelvärdet av de absoluta värdena i den tredje kolumnen. Precis som du gjorde för att beräkna medelvärdet av de initiala värdena, addera avvikelserna och dividera summan med antalet värden.


5. Tolka resultatet. Värdet på medelavvikelsen från medelvärdet är ett mått på hur nära värdena ligger varandra. Detta svarar på frågan "Hur nära medelvärdet är datavärdena i genomsnitt?"?`
Tips
- Fortsätt öva så kommer du att kunna beräkna det smidigt.
"Beräknar medelavvikelsen från medelvärdet"
Оцените, пожалуйста статью