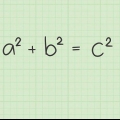Anta att vi vet att hypotenusan har en längd av 5 och en av de andra sidorna har en längd av 3. Längden på den återstående sidan är okänd. Eftersom två av sidorna är kända kan vi fortsätta med att beräkna längden på den okända sidan! Vi kommer att använda det här exemplet igen senare. Om längden på två av sidorna är okända, då måste du bestämma längden på minst en sida till för att kunna använda Pythagoras sats. De grundläggande trigonometriska funktionerna kan hjälpa dig med detta, förutsatt att du känner till en av de andra icke-räta vinklarna i triangeln. 
I vårt exempel känner vi till längden på ena sidan och hypotenusan (3 & 5), så vi skriver vår ekvation så här: 3² + b² = 5² 
I vårt exempel rutar vi 3 och 5 för att få resp. 9 och 25 att få. Vi kan nu skriva om ekvationen som 9 + b² = 25. 
I vårt exempel är ekvationen nu 9 + b² = 25. till b² subtraherar vi 9 från båda sidor av ekvationen. Detta lämnar oss med b² = 16. 
I vårt exempel, b² = 16, är ekvationen efter att ha tagit kvadratrötter b = 4. Så vi kan säga att längden på den okända sidan av vår triangel är lika med 4. 
Låt oss ta ett exempel från den verkliga världen. En stege lutar sig mot en vägg. Stegens botten är 5 meter från väggen. Stegen kommer upp till 20 meter mätt från väggens botten. Hur lång är stegen? "5 meter är avståndet till väggen” och "stegen är 20 meter hög”. Detta ger en indikation på längden på triangelns sidor. Eftersom väggen och marken är tänkta att bilda en rät vinkel och stegen är diagonal mot väggen i en vinkel, kan vi betrakta detta arrangemang som en rätvinklig triangel, vars sidor har en längd av a = 5 och b = 20. Längden på stegen är hypotenusan, den okända variabeln c. Låt oss tillämpa Pythagoras sats här: a² + b² = c² (5)² + (20)² = c² 25 + 400 = c² 425 = c² sqrt(425) = c c = 20,6 . Längden på stegen är (ungefärlig) 20,6 meter. 


Antag att vi har punkterna (6.1) och (3.5). Längden på den horisontella sidan av vår triangel är: |x1 - X2| |3 - 6| | -3 | = 3 Längden på den vertikala sidan är: |y1 - y2| |1 - 5| | -4 | = 4 Så vi kan säga att längden på sidorna i vår rätvinkliga triangel är lika med a = 3 och b = 4. 
I vårt exempel känner vi till punkterna (3,5) och (6.1), och längderna på sidorna är a= 3 och b=4, så vi bestämmer hypotenusan enligt följande: sqrt(x) betyder "kvadratroten av x". Glöm inte att alltid kontrollera dina svar. Om det ser ut som att ett svar inte är rätt, kontrollera dina beräkningar eller börja om. Om du bara känner till en sida av triangeln, men också en av de andra vinklarna (än den räta vinkeln), beräkna först en annan sida med hjälp av vad du kan om trigonometri (sin, cos, tan) eller proportionerna 30-60- 90 / 45-45-90. En annan kontroll – den längsta sidan motsätter sig den största vinkeln och den kortaste sidan mot den minsta vinkeln.
Använder pythagoras sats
Pythagoras sats beskriver längden på sidorna i en rätvinklig triangel på ett sätt så elegant och praktiskt att det fortfarande används i stor utsträckning idag. Detta anger att för varje rätvinklig triangel är summan av kvadraterna på de räta sidorna lika med kvadraten på hypotenusan. Med andra ord, för en rätvinklig triangel (en triangel med sidor som är vinkelräta mot varandra), med sidor av längden a och b och en hypotenusa med längden c: a + b = c. Pythagoras sats är en av geometrins pelare och har många praktiska tillämpningar – med hjälp av denna sats är det till exempel mycket lätt att hitta avståndet mellan två punkter i ett plan.
Steg
Metod 1 av 2: Längden på sidorna i en rätvinklig triangel

1. Kontrollera om du har att göra med en rätvinklig triangel. Pythagoras sats kan bara användas för rätvinkliga trianglar, så innan du fortsätter är det viktigt att fastställa att din triangel uppfyller definitionen av en rätvinklig triangel. Lyckligtvis finns det bara en avgörande faktor här - ett av triangelns hörn måste vara en 90-graders vinkel.
- En ledtråd är att räta vinklar ofta markeras med en liten hakparentes för att indikera att detta är en 90 graders vinkel. Se om det finns en sådan konsol i ett av hörnen på din triangel.

2. Tilldela variablerna a, b och c till sidorna av din triangel. I Pythagoras sats hänvisar variablerna a och b till de högra sidorna av din triangel, och variabeln c till hypotenusan – långsidan mitt emot den räta vinkeln. Så till att börja med tilldelar du variablerna a och b (ordningen spelar ingen roll) till de raka sidorna och du tilldelar c till hypotenusan.

3. Bestäm vilken sida av triangeln du vill veta. Pythagoras sats låter dig hitta längden på vilken sida som helst i en triangel, förutsatt att två av sidorna är kända. Bestäm vilken av sidorna som har en okänd längd--a, b, och/ellerc. Om bara en är okänd kan du gå vidare.

4. Beräkna med hjälp av ekvationen och de kända. Infoga värdena för längderna på sidorna av din triangel i ekvationen a + b = c. Kom ihåg att a och b är de raka sidorna och c är hypotenusan.

5. Räkna ut kvadraterna. För att lösa din ekvation, börja med att kvadrera var och en av de kända sidorna. Om du tycker att det är lättare kan du lämna kraften och torgföra den senare.

6. Isolera den okända variabeln på ena sidan av likhetstecknet. Alternativt kan du använda vanliga algebraiska operationer för att få det okända till ena sidan av likhetstecknet och kvadraterna till den andra sidan. Om du försöker hitta hypotenusan är c redan i positionen på ena sidan, så du kan hoppa över det steget.

7. Ta kvadratroten från båda sidor av ekvationen. Du bör nu ha en kvadrat (variabel) på ena sidan av ekvationen och ett tal på den andra sidan. Subtrahera nu kvadratroten på båda sidorna för att hitta längden på det okända.

8. Använd Pythagoras sats i praktiken. Anledningen till att Pythagoras sats används så mycket är att den är tillämpbar för att lösa många praktiska problem. Lär dig känna igen räta trianglar i världen omkring dig – varhelst du kan identifiera en rätvinklig triangel med ett eller flera objekt, kan Pythagoras sats användas för att hitta längden på en av sidorna, förutsatt att det finns två sidor eller vinklar.
Metod 2 av 2: Beräkna avståndet mellan två punkter i planet

1. Definiera två punkter i planet. Pythagoras sats kan mycket enkelt användas för att bestämma avståndet i en rät linje mellan två punkter i planet. Allt du behöver är x- och y-koordinaterna för två valfria punkter. Vanligtvis skrivs dessa koordinater som (x, y).
- För att hitta avståndet mellan dessa två punkter, betraktar vi var och en av punkterna som en av hörnen i en rätvinklig triangel, som inte tillhör den räta vinkeln. Detta gör det mycket enkelt att hitta längden på a och b, varefter c (hypotenusan och avståndet mellan de två punkterna) kan beräknas.

2. Rita de två punkterna på en graf. I ett X-Y-plan, för varje punkt (x, y), är x en punkt på den horisontella x-axeln och y är en punkt på den vertikala y-axeln. Du kan hitta avståndet mellan de två utan att plotta dem, men om du gör det får du en visuell referens för att kontrollera om ditt svar är vettigt.

3. Hitta längden på de raka sidorna av din triangel. Genom att betrakta dina två punkter som vinklarna på triangeln intill hypotenusan, kan du hitta längderna på sidorna a och b. Du kan göra detta genom att använda diagrammet eller genom att använda formlerna |x1 - X2| för den horisontella sidan och |y1 - y2| för den vertikala sidan, där (x1,y1) är den första punkten och (x2,y2) den andra punkten.

4. Använd Pythagoras sats för att hitta hypotenusan. Avståndet mellan de två punkterna är längden på triangelns hypotenusa. Använd Pythagoras sats för att hitta hypotenusan för triangeln, med sidorna a, b och c.
- (3)²+(4)²= c²
- c= sqrt(9+16)
- c= sqrt(25)
- c=5. Avståndet mellan (3,5) och (6,1) är 5.
Tips
- Om triangeln inte är en rätvinklig triangel kan du inte bara använda Pythagoras sats.
- Hypotenusan är alltid:
- linjen mittemot den räta vinkeln
- den längsta sidan av den räta triangeln
- variabeln c i Pythagoras sats
"Använder pythagoras sats"
Оцените, пожалуйста статью