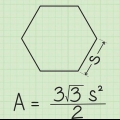
Till exempel har du en hexagon med en längd på 8 cm för sidan. Basen för en liksidig triangel är därför 8 cm. 
Till exempel, om basen för den liksidiga triangeln är 8 cm, så är basen av en rätvinklig triangel - när du delar triangeln i två räta trianglar - nu lika med 4 cm. 
Till exempel, om den räta triangeln har en hypotenusa på  ena sidan av
ena sidan av  och en annan sida av ungefär
och en annan sida av ungefär  (
( ), då säger Pythagoras sats det
), då säger Pythagoras sats det  , vilket är korrekt när du räknar ut detta:
, vilket är korrekt när du räknar ut detta:  .
. 
Till exempel, om längden på basen är 4, skulle din formel se ut så här:  .
. 
Till exempel, om längden på sidan av hexagonen är 8 cm, är längden på hypotenusan i den räta triangeln också 8 cm. Så din formel kommer nu att se ut så här:  .
. 
Till exempel, efter att ha kvadrerat de kända värdena kommer din formel att se ut så här:  .
. 
Till exempel:



Till exempel med hjälp av en miniräknare du räknar  . Så den saknade längden på den räta triangeln, och därmed längden på hexagonens apotem, är lika med 6,93 cm.
. Så den saknade längden på den räta triangeln, och därmed längden på hexagonens apotem, är lika med 6,93 cm. 

Till exempel, för en hexagon med en sidolängd på 8 cm, skulle formeln se ut så här:  .
. 
Till exempel:  .
. 
Till exempel,  , med vilken formeln nu ser ut så här:
, med vilken formeln nu ser ut så här:  .
. 
Till exempel är tangenten för 30 ungefär 0,577, så formeln skulle se ut så här:  .
. 
Till exempel:



Så apotemet för en vanlig hexagon med sidor på 8 cm är cirka 6,93 cm.
Beräkna apotem av en hexagon
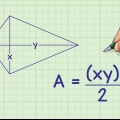
En hexagon är en polygon med sex vinklar och sidor. När en hexagon är regelbunden har den sex lika sidor och en apotem. En apotem är ett linjesegment från mitten av en polygon till mitten av varje sida. Vanligtvis måste längden på apotem anges för att beräkna arean av en hexagon. Så länge du vet längden på sidan av hexagonen, kan du beräkna längden på apotem.
Steg
Metod 1 av 2: Använd Pythagoras sats (radielängd anges)

1. Dela hexagonen i sex kongruenta liksidiga trianglar. För att göra detta, rita en linje från varje vertex eller punkt, till motsatt vertex.

2. Välj en triangel och skriv ner längden på basen. Det är lika med längden på sidan av hexagonen.

3. Gör två räta trianglar. Du gör detta genom att dra en linje från den liksidiga triangelns övre hörn vinkelrät mot basen. Denna linje kommer att halvera triangelns bas (så det är hexagonens apotem). Märk längden på basen av en av de räta trianglarna.

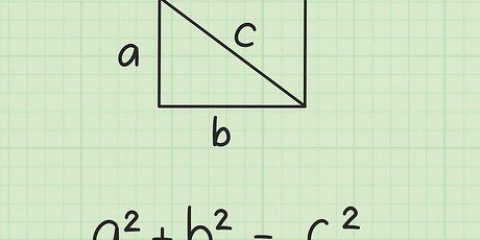
4. Använd Pythagoras sats. Formeln är  , varigenom
, varigenom  är lika med längden på hypotenusan (sidan mitt emot den räta vinkeln), och
är lika med längden på hypotenusan (sidan mitt emot den räta vinkeln), och  och
och  vara lika med längden på de andra två sidorna av triangeln.
vara lika med längden på de andra två sidorna av triangeln.
 , varigenom
, varigenom  är lika med längden på hypotenusan (sidan mitt emot den räta vinkeln), och
är lika med längden på hypotenusan (sidan mitt emot den räta vinkeln), och  och
och  vara lika med längden på de andra två sidorna av triangeln.
vara lika med längden på de andra två sidorna av triangeln. ena sidan av
ena sidan av  och en annan sida av ungefär
och en annan sida av ungefär  (
( ), då säger Pythagoras sats det
), då säger Pythagoras sats det  , vilket är korrekt när du räknar ut detta:
, vilket är korrekt när du räknar ut detta:  .
.
5. Ersätt längden på basen av den räta triangeln i formeln. Ersättning för  .
.
 .
. .
.
6. Ersätt längden på hypotenusan i formeln. Du vet längden på hypotenusan eftersom du vet längden på sexhörningen. Längden på sidan av en vanlig hexagon är lika med radien på hexagonen. Radien är en linje som förbinder mitten av en polygon med en av dess hörn. Du kommer att se att hypotenusan för den räta triangeln också är radien på sexhörningen, så längden på sidan av sexhörningen är lika med längden på hypotenusan.
 .
.
7. Kvadra de kända värdena av formeln. Kom ihåg att att kvadrera ett tal är detsamma som att multiplicera det talet med sig självt.
 .
.
8. Isolera den okända variabeln. Det gör du genom att subtrahera det kvadratiska värdet  från båda sidor av ekvationen.
från båda sidor av ekvationen.
 från båda sidor av ekvationen.
från båda sidor av ekvationen.


9. Lösa åt a  . Det gör du genom att bestämma kvadratroten av varje sida av ekvationen. Detta ger dig längden på den saknade sidan av triangeln, vilket är lika med längden på hexagonens apotem.
. Det gör du genom att bestämma kvadratroten av varje sida av ekvationen. Detta ger dig längden på den saknade sidan av triangeln, vilket är lika med längden på hexagonens apotem.
 . Det gör du genom att bestämma kvadratroten av varje sida av ekvationen. Detta ger dig längden på den saknade sidan av triangeln, vilket är lika med längden på hexagonens apotem.
. Det gör du genom att bestämma kvadratroten av varje sida av ekvationen. Detta ger dig längden på den saknade sidan av triangeln, vilket är lika med längden på hexagonens apotem. . Så den saknade längden på den räta triangeln, och därmed längden på hexagonens apotem, är lika med 6,93 cm.
. Så den saknade längden på den räta triangeln, och därmed längden på hexagonens apotem, är lika med 6,93 cm.Metod 2 av 2: Använd trigonometri (och en given radie)

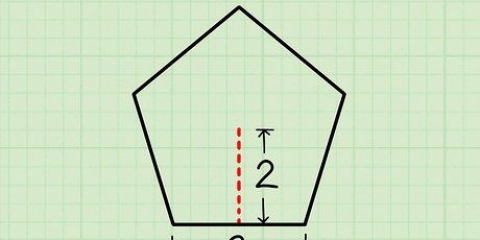
1. Skriv formeln för att hitta apotem för en vanlig polygon. Formeln är  , varigenom
, varigenom  är lika med längden på sidan av polygonen och
är lika med längden på sidan av polygonen och  är lika med antalet sidor i polygonen.
är lika med antalet sidor i polygonen.
 , varigenom
, varigenom  är lika med längden på sidan av polygonen och
är lika med längden på sidan av polygonen och  är lika med antalet sidor i polygonen.
är lika med antalet sidor i polygonen.
2. Ersätt längden på sidan i formeln. Glöm inte att ersätta variabeln  .
.
 .
. .
.
3. Ange antalet sidor i formeln. En hexagon har 6 sidor. Glöm inte att ersätta variabeln  .
.
 .
. .
.
4. Avrunda beräkningen inom parentes. Detta ger dig antalet grader som behövs för att beräkna tangenten.
 , med vilken formeln nu ser ut så här:
, med vilken formeln nu ser ut så här:  .
.
5. Bestäm tangenten. Använd en miniräknare eller trigonometrisk tabell för detta.
 .
.
6. Multiplicera tangenten med 2 och dividera sedan längden på en sida med detta tal. Med detta har du beräknat längden på apotem av din hexagon.



Så apotemet för en vanlig hexagon med sidor på 8 cm är cirka 6,93 cm.
Tips
- Termen "apothema" kan syfta på det faktiska linjesegmentet eller till längden på det linjesegmentet.
- Kom ihåg att den här metoden bara fungerar för vanliga hexagoner. Oregelbundna hexagoner har ingen apotem.
"Beräkna apotem av en hexagon"
Оцените, пожалуйста статью