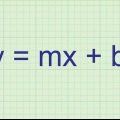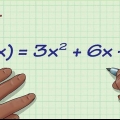Derivatan av en exponent är exponenten gånger potensen -1 av ett tal. Så derivatan av x är 5x och derivatan av x är 3.5x. Om det redan finns ett tal framför x:et, multiplicera det med exponenten. Till exempel: derivatan av 3x är 12x. Derivatan av en konstant är noll. Så derivatan av 8 är 0. Derivatan av en summa är summan av varje enskild derivata. Till exempel: derivatan av x + 3x är 3x + 6x. En produkts derivata är den första faktorn gånger derivatan av den andra faktorn plus den andra faktorn gånger derivatan av den första. Till exempel är derivatan av x(2x + 1) x(2) + (2x + 1)3x, vilket är lika med 8x + 3x. Derivaten av en kvot (säg, f/g) är [g(derivata av f) - f(derivata av g)]/g. Till exempel: derivatan av (x + 2x - 21)/(x - 3) är (x - 6x + 15)/(x - 3). 






Att bestämma en derivata
Derivater kan användas för att bestämma användbara egenskaper hos en graf, såsom maxima, minima, toppar och dalar och sluttningar. Du kan till och med använda dem för att rita komplexa ekvationer utan en grafräknare! Tyvärr är det ofta en svår uppgift att bestämma derivatan av en ekvation, men den här artikeln hjälper dig med ett antal tips och tricks.
Steg

1. Förstå notationen för en derivata. Följande två sätt att notera är de vanligaste, men många andra sätt kan hittas på Wikipedia.
- Leibniz Notation Denna notation används oftast när ekvationen innehåller ay och x. Dy/dx betyder bokstavligen "derivatan av y med avseende på x". Försök att tänka på det som Δy/Δx för värdena av x och y där skillnaden är oändlig. Denna förklaring ger naturligtvis definitionen av en gräns med avseende på derivatan: limh->0 (f(x+h)-f(x))/h. Använd denna notation på andraderivatan, skriv: dy/dx.
- Lagranges notation Derivatan av en funktion f skrivs också som f`(x). Denna notation uttalas som "funktionen f för x". Denna notation är kortare än Leibniz och används när man betraktar en derivata som en funktion. För högre derivator lägg bara till en annan " ` " redo för "f", får andraderivatan att se ut som f``(x).

2. Förstå vad ett derivat är och vad det används till. Först, för att hitta lutningen på en linjär graf, tas två punkter på linjen och dessa koordinater infogas i ekvationen (y2 - y1)/(X2 - X1). Men detta är bara möjligt med linjära grafer. För andragradsekvationer och högre är grafen en kurva, så skillnaden mellan två punkter är inte tillräckligt exakt. För att hitta lutningen för en tangent till en parabel tas två punkter och fylls i i ekvationen, för att bestämma lutningen på en krökt linje: [f(x + dx) - f(x)]/dx. Dx betyder"delta x," vad är skillnaden mellan de två x-koordinaterna för de två punkterna i grafen. Observera att denna ekvation är densamma som (y2 - y1)/(X2 - X1), men i en annan form. Eftersom det redan är känt att resultatet inte kommer att vara korrekt, väljs en indirekt approximation. För att hitta lutningen på tangenten i punkten (x, f(x)), måste dx närma sig 0 så att de två valda punkterna är nästan lika.Men du kan inte dividera med 0, så efter att ha fyllt i värdena för de två punkterna måste du eliminera dedx i nämnaren. Om detta lyckas, gör dx lika med 0 och lös. Detta är lutningen på tangenten vid (x, f(x)). Derivatan av en ekvation är den allmänna ekvationen för att hitta lutningen av någon tangent i en graf. Detta kan tyckas mycket svårt, men exemplen nedan visar hur du bestämmer derivatan.
Metod 1 av 4: Explicit differentiering

1. Använd explicit differentiering om y redan finns på ena sidan av ekvationen.

2. Byt ut en ekvation med en annan ekvation [f(x + dx) - f(x)]/dx. Till exempel, ekvationen y = x, vars derivata är [(x + dx) - x]/dx.

3. Expandera dx ytterligare för att få ekvationen [dx(2x + dx)]/dx. Nu är det möjligt att eliminera dx i täljaren och nämnaren. Resultatet är 2x + dx, och när dx närmar sig 0 blir derivatan 2x. Detta är lutningen av någon tangent till grafen y = x är 2x. Ange bara värdet på en given punkt x som du vill hitta tangenten till i ekvationen.

4. Lär dig känna igen mönstren för samma typ av ekvationer. Nedan hittar du några.
Metod 2 av 4: Implicit differentiering

1. Använd implicit differentiering när din ekvation inte enkelt kan skrivas med y på ena sidan av likhetstecknet. Även om du skriver det med y på ena sidan, skulle det fortfarande vara jobbigt att beräkna dy/dx. Nedan är ett exempel på hur man löser den här typen av ekvationer.

2. I detta exempel, xy + 2y = 3x + 2y, ersätt jey med f(x), så att det är tydligt att detta faktiskt är en funktion. Ekvationen blir då xf(x) + 2[f(x)] = 3x + 2f(x).

3. För att hitta derivatan av denna ekvation, differentiera (ett imponerande ord för att hitta derivatan) dina båda sidor av ekvationen med avseende på x. Ekvationen blir då xf`(x) + 2xf(x) + 6[f(x)]f`(x) = 3 + 2f`(x).

4. Byt ut f(x) igen med y. Var försiktig så att du inte gör detta med f`(x) eftersom detta skiljer sig mycket från f(x).

5. Lös för f`(x). Svaret i detta exempel är (3 - 2xy)/(x + 6y - 2).
Metod 3 av 4: Högre derivat

1. Att ta den högre derivatan av en funktion betyder bara att ta derivatan av derivatan. Till exempel, om den tredje derivatan frågas, tar du derivatan av derivatan av derivatan. För vissa ekvationer blir en högre derivata lika med 0.
Metod 4 av 4: Kedjeregeln

1. Om y är en differentierbar funktion av z, och z är en differentierbar funktion av x, så är y en sammansatt funktion av x, och derivatan av y med avseende på x (dy/dx) är (dy/du)*(du) /dx). Kedjeregeln kan också vara en sammansatt ekvation, så här: (2x - x). För att hitta derivatan av detta; tänk bara på samma sätt som du gör med produktlinjen. Multiplicera ekvationen med exponenten och reducera exponenten med 1. Multiplicera sedan ekvationen med derivatan som faller under exponenten (i detta fall 2x^4 - x). Svaret på detta problem blir då 3(2x - x)(8x - 1).
Tips
- När du ser ett till synes olösligt problem, oroa dig inte. Försök dela upp problemet i mindre delar genom att tillämpa produktreglerna, kvotregeln osv. Särskilj sedan de enskilda delarna.
- Öva produktregeln, kvotregeln, kedjeregeln och viktigast av allt implicit differentiering eftersom dessa kan vara ganska knepiga från kalkyl.
- Känn din miniräknare; prova de olika funktionerna i din miniräknare för att lära dig hur de fungerar. Det är verkligen värdefullt att veta hur man använder tangent- och derivatfunktionerna, om din miniräknare har dem.
- Memorera de vanligaste trigonometriska derivaten och hur man arbetar med dem.
Varningar
- Kom ihåg att minustecknet står framför f(derivatan eller g) när du använder kvotregeln; detta är ett vanligt misstag och kommer att resultera i ett felaktigt svar.
Оцените, пожалуйста статью