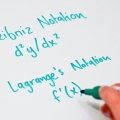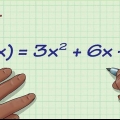Hur man bestämmer lutningen på en linje

Steg

Lutningen på en linje är ett mått på hur snabbt linjen ändras. Detta kan göras med en rak linje -- där lutningen talar om exakt hur långt upp (positiv lutning) eller ner (negativ lutning) en linje går över ett visst avstånd. Lutningen kan också användas för en tangent till en kurva. Eller det kan vara en krökt linje, som används i analys, där lutningen också är känd som "derivatan" av en funktion. Hur som helst, tänk bara på lutningen som "förändringshastigheten" för en graf: om variabeln "x" blir större, med vilken hastighet ändras "y"?? Det är ett sätt att tänka på lutningen som en orsak och verkan.

Steg

Metod 1 av 3: Hitta lutningen för en linjär ekvation

1. Använd lutningen för att avgöra hur brant och i vilken riktning (upp eller ner) en linje går. Att bestämma lutningen på en linje är lätt, så länge du har eller kan rita en linjär ekvation. Denna metod fungerar bara när:

Variablerna har inga exponenter.
Det finns bara två variabler, och ingen av dem är bråk (till exempel kan följande inte vara: $\frac{1}{X}$ ${frac{1}{x}}$ )
Ekvationen kan förenklas till formen $y = m X + b$ $y=mx+b$ , varigenom m och b konstanter (tal som 3, 10, -12, $\frac{4}{3}, \frac{3}{5}$ ${frac{4}{3}},{frac{3}{5}}$ ).

2. Hitta talet före x, vanligtvis skrivet som `m` för att bestämma lutningen. Om ekvationen redan är i rätt form,

y = m X + b

$y=mx+b$ , välj sedan talet i `m`-positionen (men om det inte finns något tal före x är lutningen 1). Så det är också lutningen! Vet att detta nummer, m, multipliceras alltid med variabeln, i detta fall ett `x`. Kolla in följande exempel:

y = 2 X + 6

$y=2x+6$

Lutning = 2

y = 2 - X

$y=2-x$

Lutning = -1

y = \frac{3}{8} X - 10

$y={frac{3}{8}}x-10$

lutning = $\frac{3}{8}$ ${frac{3}{8}}$

Bild med titeln Hitta lutningen på en ekvation Steg 3

3. Känn igen ekvationen där en variabel är isolerad om lutningen inte är tydlig. Du kan addera, subtrahera, multiplicera osv. att isolera en variabel (vanligtvis "y"). Kom ihåg att vad du än gör på ena sidan av likhetstecknet (som att lägga till 3), måste du göra detta på andra sidan också. Ditt slutliga mål är en ekvation, som

y = m X + b

$y=mx+b$ . Till exempel:

Hitta lutningen av $2 y - 3 = 8 X + 7$ $2y-3=8x+7$

Konvertera det till formuläret $y = m X + b$ $y=mx+b$ :

2 y - 3 + 3 = 8 X + 7 + 3

$2y-3+3=8x+7+3$

2 y = 8 X + 10

$2y=8x+10$

2 y 2 = 8 X + 10 2

${frac{2y}{2}}={frac{8x+10}{2}}$

y = 4 X + 5

$y=4x+5$

Bestäm lutningen:

Lutning = M = 4

Metod 2 av 3: Bestämma lutningen med två punkter

Bild med titeln Hitta lutningen på en ekvation Steg 4

1. Använd en graf och två punkter för att snabbt hitta lutningen utan ekvationen. Om du har en graf och en linje men ingen ekvation, kan du fortfarande bestämma lutningen med lätthet. Allt du behöver är två punkter på linjen, som du applicerar på ekvationen

y 2 - y_{1} X 2 - X_{1}

${frac{y_{2}-y_{1}}{x_{2}-x_{1}}}$ . När du bestämmer lutningen, tänk på följande information för att se till att du är på rätt spår:

Positiva backar går upp och till höger.
Negativa backar går ner och till höger.
Brantare backar är brantare linjer. Mindre branta backar är alltid mer gradvisa.
Perfekta horisontella linjer har en lutning på noll.
Perfekt vertikala linjer har ingen lutning alls. Deras lutning (eller lutning) är "odefinierad".

Bild med titeln Hitta lutningen på en ekvation Steg 5

2. Välj två punkter och sätt dem i den enkla (x, y) formen. Använd grafen (eller uppgiftsfrågan) för att hitta x- och y-koordinaterna för två punkter på grafen. De kan bestå av två valfria punkter som linjen passerar genom. Anta till exempel att i denna metod går linjen genom punkten (2.4) och genom (6.6).

I varje par är x-koordinaten det första talet och y-koordinaten är det andra talet efter decimalkomma.

Varje x-koordinat på en linje har en motsvarande y-koordinat.

Bild med titeln Hitta lutningen på en ekvation Steg 6

3. Märk punkterna x₁, y₁, X₂, y₂, och behåll varje poäng med sitt par. Fortsätt med vårt första exempel, använd punkterna (2.4) och (6.6), märk x- och y-koordinaterna för varje punkt. Om allt gick bra slutar du nu med:

X₁: 2

y₁: 4

X₂: 6

y₂: 6

Bild med titeln Hitta lutningen på en ekvation Steg 7

4. Ersätt dessa punkter i `punkt-lutningsformeln` för att hitta lutningen. Följande formel används för att bestämma lutningen med hjälp av två valfria punkter på en rät linje: $y 2 - y_{1} X 2 - X_{1}$ ${frac{y_{2}-y_{1}}{x_{2}-x_{1}}}$ . Byt bara ut de fyra punkterna och förenkla:

Ursprungliga poäng: (2.4) och (6.6).

Tillämpa på punkt-lutningsformeln:

6 - 4 6 - 2

${frac{6-4}{6-2}}$

Förenkla för det slutliga svaret:

$\frac{2}{4} = \frac{1}{2}$ ${frac{2}{4}}={frac{1}{2}}$ = lutning

Bild med titeln Hitta lutningen på en ekvation Steg 8

5. Förstå hur punkt-lutningsformeln fungerar. Lutningen på en linje indikeras av förändringen av y från x (y/x): hur mycket linjen går upp dividerat med hur mycket linjen fortsätter till höger. Linjens ökning är skillnaden mellan y-värdena (kom ihåg att y-axeln går upp och ner), och ökningen av linjen är skillnaden mellan x-värdena (och x-axeln går från vänster till höger).

Bild med titeln Hitta lutningen på en ekvation Steg 9

6. Lär dig andra sätt du behöver veta för att bestämma lutningen. Lutningens ekvation är

y 2 - y_{1} X 2 - X_{1}

${frac{y_{2}-y_{1}}{x_{2}-x_{1}}}$ . Detta kan också representeras av den grekiska bokstaven `Δ` (`delta`), som betyder `skillnad`. Lutningen kan också representeras som Δy/Δx, vilket betyder "skillnaden mellan y" / "skillnaden mellan x". Detta är exakt samma fråga som "Bestäm lutningen mellan.."

Metod 3 av 3: Använd differentialkalkyl för att hitta lutningen på en kurva

Bild med titeln Hitta lutningen på en ekvation Steg 10

1. Gå igenom hur du kan bestämma derivatan av vanliga funktioner på olika sätt. Derivat ger dig förändringshastigheten (eller lutningen) vid en punkt på en linje. Linjen kan vara böjd eller rak – det spelar ingen roll. Kom ihåg hur linjen ändras vid varje given tidpunkt, snarare än hur lutningen på hela linjen ändras. Hur du bestämmer derivatan beror på typen av funktion, så se över hur du bestämmer derivatan av funktioner innan du fortsätter.

Läs här om att bestämma derivatan
De enklaste derivatorna, de för standardexponentiella ekvationer, kan du enkelt hitta med en snabb metod. Du kommer att använda detta i resten av metoden.

Bild med titeln Hitta lutningen på en ekvation Steg 11

2. Förstå vilka problem som kräver att du beräknar lutningen med hjälp av derivator. Du kommer inte alltid att bli explicit tillfrågad om derivatan eller lutningen av en kurva. Du kan också bli tillfrågad om "förändringshastigheten" vid punkt (x, y). Du kan bli tillfrågad om en ekvation för grafens lutning, vilket helt enkelt betyder att hitta derivatan. Slutligen kan du bli tillfrågad om `lutningen på tangentlinjen i (x, y)`. Detta betyder återigen att den bara frågar efter kurvans lutning vid en specifik punkt (x, y).

Med den här metoden, ställ dig själv följande fråga: "Vad är lutningen på linjen

f (X) = 2 X 2 + 6 X

$f(x)=2x^{2}+6x$ i punkt (4.2)?"

Derivatan skrivs ofta som

f^{sex} (X), y^{sex},

eller

Bild med titeln Hitta lutningen på en ekvation Steg 12

3.Hitta derivatan av funktionen. Du behöver inte ens en riktig graf, bara grafens funktion eller ekvation. I detta exempel använder vi en tidigare diskuterad funktion,

4X+6 $f$

Bild med titeln Hitta lutningen på en ekvation Steg 13

4.Byt ut punkten i derivatans ekvation för att hitta lutningen. Differentialen för en funktion ger dig lutningen för funktionen vid en given punkt. Med andra ord, f"(x) är lutningen för funktionen när som helst (x,f(x)). Så för detta träningsproblem: