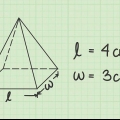
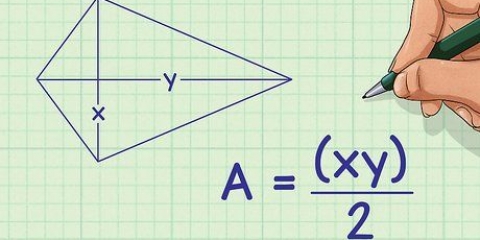Till exempel, om du vill hitta arean av en sexkantig pyramid och du vet att längden på en kant av basen är 4 cm, beräknar du  för att hitta basens omkrets, eftersom en hexagon har sex sidor. Så basens omkrets är 24 cm, så formeln för området kommer att se ut så här:
för att hitta basens omkrets, eftersom en hexagon har sex sidor. Så basens omkrets är 24 cm, så formeln för området kommer att se ut så här:  .
. 
Anta att lutningshöjden på en sexkantig pyramid är 12 cm, då kommer din formel att se ut så här:  .
. 
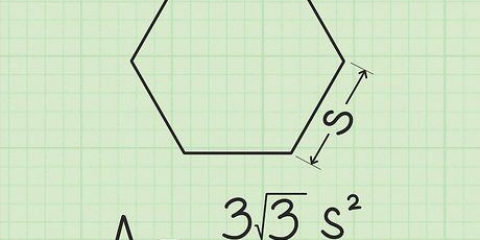
Om du till exempel har att göra med en sexkantig pyramid bör du göra det beräkna arean av hexagonen. Formeln är  , varigenom
, varigenom  är längden på en sida av hexagonen. Eftersom längden på en sida av hexagonen är 4 cm, beräkna enligt följande:
är längden på en sida av hexagonen. Eftersom längden på en sida av hexagonen är 4 cm, beräkna enligt följande:




 .
.
Så arean av basen är 41,57 kvadratcentimeter. 
Antag att arean av den sexkantiga basen är 41,57 cm. då skulle din formel för området se ut så här:  .
. 
Till exempel:




Till exempel:


Så den totala arean av en hexagonal pyramid, med en given baskantlängd på 4 cm och en sluttningshöjd på 12 cm, är lika med 185,57 kvadratcentimeter. 

Anta att längden på ena sidan av basen av en fyrkantig pyramid är 4 cm och lutningshöjden är 12 cm, då skulle formeln se ut så här:  .
. 
Till exempel:



Till exempel:





Till exempel:


Den totala arean av en fyrkantig pyramid, med en sida av basen på 4 cm och en sned höjd på 12 cm, är därför 112 kvadratcentimeter.
Bestämma arean av en pyramid
Arean av en pyramid kan hittas genom att lägga till arean av dess bas till arean av dess sidor. När du arbetar med vanliga pyramider kan du hitta arean med hjälp av en formel så länge du vet hur du hittar arean av pyramidens bas. Eftersom basen kan vara en polygon är det användbart att veta hur man bestämmer arean av former som pentagoner och hexagoner. Men när du arbetar med den vanliga vanliga fyrkantiga pyramiden är det lätt att beräkna den totala ytan, förutsatt att du vet pyramidens lutningshöjd och längden på den kvadratiska basen.
Steg
Metod 1 av 2: Hitta arean för en vanlig pyramid

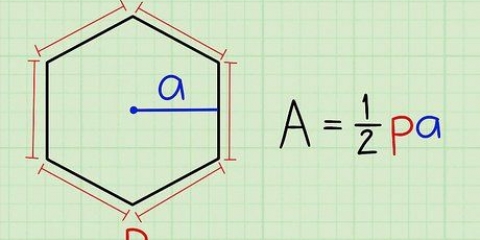
1. Skriv formeln för arean av en vanlig pyramid. Formeln är  , varigenom
, varigenom  är lika med pyramidens totala yta,
är lika med pyramidens totala yta,  är lika med basens omkrets,
är lika med basens omkrets,  är lika med lutningen på pyramiden, och
är lika med lutningen på pyramiden, och  är lika med arean av basen.
är lika med arean av basen.
 , varigenom
, varigenom  är lika med pyramidens totala yta,
är lika med pyramidens totala yta,  är lika med basens omkrets,
är lika med basens omkrets,  är lika med lutningen på pyramiden, och
är lika med lutningen på pyramiden, och  är lika med arean av basen.
är lika med arean av basen. - Grundformeln för arean av en pyramid, regelbunden eller oregelbunden, är total area = basarea + sluttande area.
- Förväxla inte "lutande höjd" med "höjd".`Sluthöjden` är det diagonala avståndet från toppen av pyramiden till kanten av basen. "Höjden" är det vinkelräta avståndet från topp till bas.

2. Beräkna omkretsen av basen. Om omkretsen inte anges, men ges längden på en kant av basen, kan du beräkna omkretsen genom att multiplicera längden på en kant med antalet kanter.
 för att hitta basens omkrets, eftersom en hexagon har sex sidor. Så basens omkrets är 24 cm, så formeln för området kommer att se ut så här:
för att hitta basens omkrets, eftersom en hexagon har sex sidor. Så basens omkrets är 24 cm, så formeln för området kommer att se ut så här:  .
.
3. Ange lutningshöjdvärdet i formeln. Se till att använda den lutande höjden, inte den vinkelräta höjden. Lutningshöjden ska anges i problemet. Om du inte känner till sluttningshöjden kan du inte använda den här metoden.
 .
.
4. Beräkna arean av basen. Hur du gör detta beror på formen på basen. För det behöver du veta hur man bestämmer områdena för polygoner.
 , varigenom
, varigenom  är längden på en sida av hexagonen. Eftersom längden på en sida av hexagonen är 4 cm, beräkna enligt följande:
är längden på en sida av hexagonen. Eftersom längden på en sida av hexagonen är 4 cm, beräkna enligt följande: 



 .
.Så arean av basen är 41,57 kvadratcentimeter.

5. Applicera arean av basen på formeln. Se till att du har variabeln  ersätter.
ersätter.
 ersätter.
ersätter. .
.
6. Multiplicera basens omkrets med pyramidens sluttande höjd. Dela produkten med två. Detta ger dig den sluttande delen av pyramidens ytor.




7. Lägg till de två värdena tillsammans. Summan är den lutande arean plus basarean, så du får den totala arean av pyramiden i kvadratenheter.


Så den totala arean av en hexagonal pyramid, med en given baskantlängd på 4 cm och en sluttningshöjd på 12 cm, är lika med 185,57 kvadratcentimeter.
Metod 2 av 2: Hitta arean av en fyrkantig pyramid

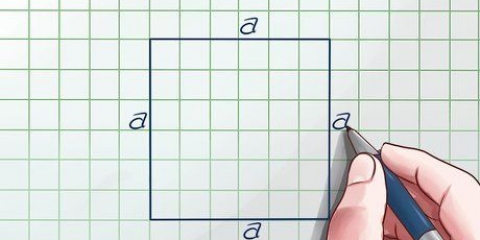
1. Skriv formeln för arean av en fyrkantig pyramid. Formeln är  , varigenom
, varigenom  är lika med längden på ena sidan av basen, och
är lika med längden på ena sidan av basen, och  är lika med lutningen på pyramiden.
är lika med lutningen på pyramiden.
 , varigenom
, varigenom  är lika med längden på ena sidan av basen, och
är lika med längden på ena sidan av basen, och  är lika med lutningen på pyramiden.
är lika med lutningen på pyramiden. - Förväxla inte "lutande höjd" med "höjd".`Sluthöjden` är det diagonala avståndet från toppen av pyramiden till kanten av basen. "Höjden" är det vinkelräta avståndet från toppen till basen.
- Observera att den här formeln bara är ett annat sätt att beräkna totalarea = basarea (
) + Lutande yta (
) att skriva. Denna formel fungerar bara för vanliga fyrkantiga pyramider.

2. Ange värdena för sidornas längd och lutningshöjd i formeln. Se till att byta ut längden på sidan av basen med  och lutningshöjden med
och lutningshöjden med  .
.
 och lutningshöjden med
och lutningshöjden med  .
. .
.
3. Kvadra längden på ena sidan av basen. Detta kommer att ge dig området för basen.



4. Multiplicera längden på ena sidan av basen med lutningshöjden och dividera med två. Multiplicera sedan med fyra. Detta kommer att ge dig den vinklade ytan på pyramiden.





5. Lägg till området på basen till det lutande området. Detta ger dig den totala ytan av pyramiden, i kvadratiska enheter.


Den totala arean av en fyrkantig pyramid, med en sida av basen på 4 cm och en sned höjd på 12 cm, är därför 112 kvadratcentimeter.
Förnödenheter
- Penna
- Papper
- Miniräknare (valfritt)
- Linjal (valfritt)
Оцените, пожалуйста статью