Till exempel, om du vill hitta bredden på en rektangel med en area på 24 cm och en längd på 8 cm, skulle din formel se ut så här:


Till exempel i ekvationen  , dela varje sida med 8.
, dela varje sida med 8.




Till exempel för en rektangel med arean på  och en längd på
och en längd på  , blir bredden
, blir bredden  .
. 
Om du till exempel vill hitta bredden på en rektangel med en omkrets på 22 cm och en längd på 8 cm, skulle formeln se ut så här:



Till exempel i ekvationen  , subtrahera 16 från varje sida och dividera med 2.
, subtrahera 16 från varje sida och dividera med 2.





Till exempel för en rektangel med en omkrets av  och en längd på
och en längd på  , blir bredden
, blir bredden  .
. 

Till exempel, när man bestämmer bredden på en rektangel med en diagonal på 5 cm och en sida på 4 cm, skulle formeln se ut så här: 

Till exempel:




Till exempel i ekvationen  , subtrahera 16 från varje sida.
, subtrahera 16 från varje sida.



Till exempel:



Till exempel för en rektangel med diagonalen på  och ena sidan av
och ena sidan av  , blir bredden
, blir bredden  .
. 

Sambandet kan ges genom att ange hur många gånger en sida är större än den andra, eller hur många enheter mer eller mindre. Till exempel kan det vara känt att längden är fem centimeter längre än bredden. Uttrycket för längden blir då  .
. 
Till exempel om du vet att arean är 24 cm, och det  , då ser formeln ut så här:
, då ser formeln ut så här:



Förenkla till exempel  fram tills
fram tills  .
. 
Du kan behöva lägga till eller subtrahera för att lösa detta, eller faktorisera eller använda en andragradsekvation för att lösa detta. Till exempel,  kan lösas upp enligt följande:
kan lösas upp enligt följande:


Du har då två möjliga lösningar på :
: eller
eller  . Eftersom en rektangel inte kan ha en negativ bredd kan du utesluta -8. Så är din lösning
. Eftersom en rektangel inte kan ha en negativ bredd kan du utesluta -8. Så är din lösning  .
.
Bestämma bredden på en rektangel
Det finns många sätt att hitta de saknade måtten på en rektangel, och metoden du använder beror på vilken data du har. Så länge arean eller omkretsen är känd, liksom längden på en sida av rektangeln (eller förhållandet mellan dess längd och bredd), kan den saknade dimensionen bestämmas. Egenskaperna för en rektangel är sådana att dessa metoder kan användas för att bestämma dess latitud eller longitud.
Steg
Metod 1 av 4: Använd arean och längden

1. Skriv ner formeln för arean av en rektangel. Formeln är  , varigenom
, varigenom  är lika med arean av rektangeln,
är lika med arean av rektangeln,  är lika med längden på rektangeln, och
är lika med längden på rektangeln, och  är lika med rektangelns bredd.
är lika med rektangelns bredd.
 , varigenom
, varigenom  är lika med arean av rektangeln,
är lika med arean av rektangeln,  är lika med längden på rektangeln, och
är lika med längden på rektangeln, och  är lika med rektangelns bredd.
är lika med rektangelns bredd. - Metoden fungerar bara för en given area och längd av rektangeln.
- Denna formel är också tillgänglig i formuläret
, varigenom
är lika med rektangelns höjd (snarare än längden). Dessa två termer hänvisar till samma dimensioner.

2. Använd värdena för area och längd i formeln. Se till att ersätta rätt variabler.


3. Lösa åt w  . Du gör detta genom att dividera varje sida av ekvationen med dess längd.
. Du gör detta genom att dividera varje sida av ekvationen med dess längd.
 . Du gör detta genom att dividera varje sida av ekvationen med dess längd.
. Du gör detta genom att dividera varje sida av ekvationen med dess längd. , dela varje sida med 8.
, dela varje sida med 8.



4. Skriv ner ditt slutliga svar. Glöm inte att nämna enheten för avläsningarna.
 och en längd på
och en längd på  , blir bredden
, blir bredden  .
.Metod 2 av 4: Använd omkretsen och längden
1. Skriv formeln för omkretsen av en rektangel. Formeln är  , varigenom
, varigenom  är lika med rektangelns omkrets,
är lika med rektangelns omkrets,  är lika med längden på rektangeln, och
är lika med längden på rektangeln, och  är lika med rektangelns bredd.
är lika med rektangelns bredd.
 , varigenom
, varigenom  är lika med rektangelns omkrets,
är lika med rektangelns omkrets,  är lika med längden på rektangeln, och
är lika med längden på rektangeln, och  är lika med rektangelns bredd.
är lika med rektangelns bredd.- Denna metod fungerar bara för en given omkrets och längd av rektangeln.
- Denna formel skrivs också som
, varigenom
är lika med rektangelns höjd och används istället för längden. Variablerna
och
refererar till samma dimensioner, och den fördelande egenskapen dikterar att dessa två formler, även om de är olika sorterade, ger samma resultat.

2. Använd omkretsen och längden i formeln. Se till att ersätta rätt variabler.



3. Lösa w  . För att göra detta måste du subtrahera längden från varje sida av ekvationen och dividera den med 2.
. För att göra detta måste du subtrahera längden från varje sida av ekvationen och dividera den med 2.
 . För att göra detta måste du subtrahera längden från varje sida av ekvationen och dividera den med 2.
. För att göra detta måste du subtrahera längden från varje sida av ekvationen och dividera den med 2. , subtrahera 16 från varje sida och dividera med 2.
, subtrahera 16 från varje sida och dividera med 2.




4. Skriv ner det slutliga svaret. Glöm inte att nämna enheten för avläsningarna.
 och en längd på
och en längd på  , blir bredden
, blir bredden  .
.Metod 3 av 4: Använd diagonalen och längden

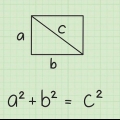
1. Skriv ner formeln för en rektangels diagonal. Formeln är  , varigenom
, varigenom  är lika med längden på diagonalen,
är lika med längden på diagonalen,  är lika med längden och
är lika med längden och  är lika med rektangelns bredd.
är lika med rektangelns bredd.
 , varigenom
, varigenom  är lika med längden på diagonalen,
är lika med längden på diagonalen,  är lika med längden och
är lika med längden och  är lika med rektangelns bredd.
är lika med rektangelns bredd. - Denna metod fungerar bara för en given längd av diagonalen och längden på en sida av rektangeln.
- Denna formel skrivs också som
, varigenom
är lika med rektangelns höjd och används istället för längden. Variablerna
och
hänvisa till samma avläsningar.

2. Ersätt värdena för diagonalen och sidan i formeln. Se till att ersätta rätt variabler.


3. Kvadra båda sidor av formeln. Du måste göra detta för att bli av med det radikala tecknet så att det blir lättare att isolera breddvariabeln.




4. Isolera variabeln w  . Du gör detta genom att subtrahera den kvadratiska längden, från varje sida av ekvationen.
. Du gör detta genom att subtrahera den kvadratiska längden, från varje sida av ekvationen.
 . Du gör detta genom att subtrahera den kvadratiska längden, från varje sida av ekvationen.
. Du gör detta genom att subtrahera den kvadratiska längden, från varje sida av ekvationen. , subtrahera 16 från varje sida.
, subtrahera 16 från varje sida.


5. Lösa åt w  . Det gör du genom att bestämma kvadratroten för varje sida av ekvationen.
. Det gör du genom att bestämma kvadratroten för varje sida av ekvationen.
 . Det gör du genom att bestämma kvadratroten för varje sida av ekvationen.
. Det gör du genom att bestämma kvadratroten för varje sida av ekvationen.


6. Skriv ner det slutliga svaret. Glöm inte att nämna enheten för avläsningarna.
 och ena sidan av
och ena sidan av  , blir bredden
, blir bredden  .
.Metod 4 av 4: Använd arean eller omkretsen och relativ längd

1. Skriv ner formeln för arean eller omkretsen av en rektangel. Vilken formel du använder beror på de givna mätvärdena. Om arean anges, använd areaformeln. Om omkretsen är angiven, använd omkretsformeln.
- Om området eller omkretsen är okänd, eller förhållandet mellan längden och bredden, kan du inte använda denna metod.
- Formeln för området är
.
- Formeln för omkretsen är
.
- Till exempel, kanske med tanke på att arean av en rektangel är 24 cm, då använder du formeln för arean av en rektangel.

2. Skriv uttrycket som beskriver förhållandet mellan längden och bredden. Skriv ditt uttryck i en jämförelse med  .
.
 .
. .
.
3. Byt ut variabeln l  i arean eller omkretsformeln med uttrycket för längden. Formeln hör nu bara variabeln
i arean eller omkretsformeln med uttrycket för längden. Formeln hör nu bara variabeln  vilket innebär att du kan beräkna bredden.
vilket innebär att du kan beräkna bredden.
 i arean eller omkretsformeln med uttrycket för längden. Formeln hör nu bara variabeln
i arean eller omkretsformeln med uttrycket för längden. Formeln hör nu bara variabeln  vilket innebär att du kan beräkna bredden.
vilket innebär att du kan beräkna bredden. , då ser formeln ut så här:
, då ser formeln ut så här:


4. Förenkla ekvationen. Den förenklade ekvationen kan ha olika former, beroende på förhållandet mellan längden och bredden, och beroende på om du går för arean eller omkretsen. Försök att göra en jämförelse med vilken du  kan lösa så enkelt som möjligt.
kan lösa så enkelt som möjligt.
 kan lösa så enkelt som möjligt.
kan lösa så enkelt som möjligt. fram tills
fram tills  .
.
5. Lösa åt w  . Återigen, hur gör du
. Återigen, hur gör du  löser beror på den förenklade ekvationen. Använd de grundläggande reglerna för algebra och geometri för att lösa detta.
löser beror på den förenklade ekvationen. Använd de grundläggande reglerna för algebra och geometri för att lösa detta.
 . Återigen, hur gör du
. Återigen, hur gör du  löser beror på den förenklade ekvationen. Använd de grundläggande reglerna för algebra och geometri för att lösa detta.
löser beror på den förenklade ekvationen. Använd de grundläggande reglerna för algebra och geometri för att lösa detta. kan lösas upp enligt följande:
kan lösas upp enligt följande:

Du har då två möjliga lösningar på
 :
: eller
eller  . Eftersom en rektangel inte kan ha en negativ bredd kan du utesluta -8. Så är din lösning
. Eftersom en rektangel inte kan ha en negativ bredd kan du utesluta -8. Så är din lösning  .
. "Bestämma bredden på en rektangel"
Оцените, пожалуйста статью