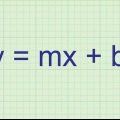(3-5)/(8-2) = -2/6 = -1/3 Linjens lutning är -1/3. För att hitta denna lutning måste du förenkla 2/6 till dess minsta värden, 1/3, eftersom både 2 och 6 är delbara med 2. 
Den negativa reciproka av -1/3 är 3 eftersom 3/1 är den reciproka av 1/3 och tecknet har ändrats från negativt till positivt. 

3 --> y = mx + b = y = 3x + b 
(5, 4) --->y = 3x + b = 4 = 3(5) + b = 4 = 15 + b 
4 = 15 + b = -11 = b b = -11 
y = mx + b y = 3x - 11 Ekvationen för den vinkelräta halveringslinjen genom punkterna (2, 5) och (8, 3) är y = 3 x - 11.
Bestämma den vinkelräta bisektrisen av två punkter
En vinkelrät bisektrik är en linje som delar ett segment som är förenat med två punkter i en vinkel på 90 grader. För att hitta den vinkelräta bisektrisen för två punkter behöver du bara hitta deras mittpunkter och den reciproka, och sedan tillämpa svaren på ekvationen för en linje med formen y = mx + b. Om du vill veta hur man hittar den vinkelräta halveringslinjen för två punkter, följ stegen nedan.
Steg
Metod 1 av 2: Samla information

1. Hitta mitten av de två punkterna. Hitta mittpunkten för två punkter genom att tillämpa punkterna på mittpunktsformeln: [(X1 + X2)/2,( y1 + y2)/2]. Detta innebär att du medelvärdet av x- och y-koordinaterna för de två punkterna, vilket ger dig mitten av de två koordinaterna. Anta att vi arbetar med koordinaterna (x1, y1) av (2, 5) och koordinaterna (x2, y2) från (8, 3). Du bestämmer mitten av de två punkterna enligt följande:
- [(2+8)/2, (5 +3)/2] =
- (10/2, 8/2) =
- (5, 4)
- Koordinaterna för mitten av (2, 5) och (8, 3) är (5, 4).

2. Hitta lutningen för de två punkterna. För att hitta lutningen (lutningen) för de två punkterna, tillämpa punkterna på lutningsformeln: (y2 - y1) / (x2 - X1). En linjes lutning är avståndet för en vertikal förändring över avståndet för en motsvarande horisontell förändring. Du bestämmer linjens lutning genom punkterna (2, 5) och (8, 3) enligt följande:

3. Hitta den negativa ömsesidiga lutningen av de två punkterna. För att hitta den negativa reciproka av en sluttning, ta den reciproka av lutningen och ändra tecknet. Du kan hitta den reciproka av ett tal genom att invertera x- och y-koordinaterna. Den negativa reciproka 1/2 är -2/1, eller bara -2; den reciproka av -4 är 1/4.
Metod 2 av 2: Beräkna linjens ekvation

1. Skriv ekvationen för en linje på formen y = mx + b. Ekvationen för en linje genom två punkter är av formen `y = mx + b ` där x- och y-koordinaterna på linjen representeras av `x` och `y`, `m` representerar linjens lutning och `b` representerar linjens skärning med y-axeln. När du har skrivit denna ekvation kan du börja hitta ekvationen för den vinkelräta bisektrisen av de två punkterna.

2. Tillämpa den negativa reciproka av den ursprungliga lutningen på ekvationen. Den negativa ömsesidiga lutningen av punkterna (2, 5) och (8, 3) var 3. "m" i ekvationen representerar lutningen, så ange 3 för "m" i ekvationen för en rät linje, y = mx + b.

3. Applicera mittpunkten på linjen. Du vet redan att mittpunkterna för punkterna (2, 5) och (8, 3) är lika med (5, 4). Eftersom den vinkelräta bisektaren passerar genom mittpunkterna på de två linjerna, kan du tillämpa koordinaterna för mittpunkterna på linjens ekvation. Fyll bara i (5, 4) istället för linjens x- och y-koordinater.

4. Lös för korsningen. Du har hittat tre av de fyra variablerna i linjens ekvation. Nu har du tillräckligt med information för att bestämma den återstående variabeln `b`, skärningspunkten mellan denna linje och y-axeln. Isolera variabeln `b` för att bestämma dess värde. Subtrahera 15 från båda sidor av ekvationen.

5. Skriv ekvationen för den vinkelräta halveringslinjen. För att skriva ekvationen för den vinkelräta halveringslinjen, ersätt lutningen för linjen (3) och skärningspunkten med y-axeln (-11) i ekvationen av formen y = mx + b. Ange inget för x- och y-koordinaterna, för med denna ekvation kan du hitta vilken koordinat som helst på linjen genom att fylla i en x- eller en y-koordinat.
"Bestämma den vinkelräta bisektrisen av två punkter"
Оцените, пожалуйста статью