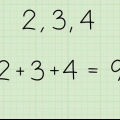Bestämma den tredje vinkeln i en triangel

Steg
Varningar

Att bestämma den tredje vinkeln i en triangel om du vet vad de andra två vinklarna är är lätt. Allt du behöver göra är att subtrahera de andra vinklarna från 180° för att hitta den tredje vinkeln. Det finns dock några andra sätt att bestämma den tredje vinkeln i en triangel, beroende på vilket problem du arbetar med. Om du vill lära dig hur du bestämmer det där lysande tredje hörnet i en triangel, läs steg 1 för att komma igång.

Steg

Metod 1 av 3: Använd de två andra hörnen

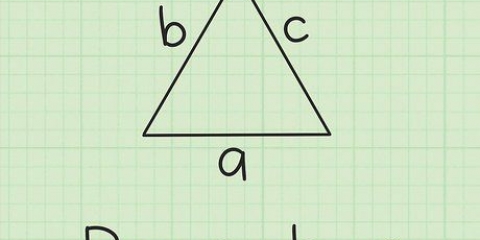
1. Lägg ihop de två kända vinklarna. Allt du behöver veta är att alla vinklar i en triangel går ihop alltid vara 180°. Detta är alltid sant. Så om du känner till två av triangelns tre hörn så saknar du bara en liten pusselbit. Det första du kan göra är att lägga ihop de vinklar du redan känner till. I det här exemplet är vinklarna du känner till 80° och 65°. Lägg ihop dem (80° + 65°) för att få 145°.

Bild med titeln Hitta den tredje vinkeln i en triangel Steg 2

2. Subtrahera detta tal från 180°. Vinklarna i en triangel adderas 180°. Därför måste den återstående vinkeln tillsammans med de andra vinklarna är 180°. I detta exempel: 180° - 145° = 35°.

Bild med titeln Hitta den tredje vinkeln i en triangel Steg 3

3. Skriv ner ditt svar. Du vet nu att den tredje vinkeln är 35°. Om du är osäker, kolla bara ditt arbete. De tre vinklarna tillsammans ska vara 180°, annars är det ingen triangel. 80° + 65° + 35° = 180°. Nu är du redo.

Metod 2 av 3: Använda variabler

Bild med titeln Hitta den tredje vinkeln i en triangel Steg 4

1. Skriv ner problemet. Ibland har du inte så tur och du vet inte värdena för de två vinklarna i en triangel, men du har bara några få variabler, eller några variabler och en vinkel. Låt oss säga att du har att göra med följande problem: Bestäm vinkeln `x` för triangeln med måtten `x`, `2x` och 24°. Skriv bara ner detta först.

Bild med titeln Hitta den tredje vinkeln i en triangel Steg 5

2. Lägg till alla dimensioner. Det är samma princip som du skulle följa om du kände till de två vinklarna. Matcha bara värdena på vinklarna genom att kombinera variablerna. Så, x + 2x + 24° = 3x + 24°.

Bild med titeln Hitta den tredje vinkeln i en triangel Steg 6

3. Subtrahera dessa värden från 180°. Subtrahera sedan dessa värden från 180° för att komma närmare att lösa problemet. Se till att ekvationen är lika med 0. Så här ser det ut:

180° - (3x + 24°) = 0

180° - 3x - 24° = 0

156° - 3x = 0

Bild med titeln Hitta den tredje vinkeln i en triangel Steg 7

4. Lös nu för x. Flytta nu variablerna till ena sidan av ekvationen och talen till den andra sidan. Du får 156° = 3x. Dela nu båda sidor av ekvationen med 3 för att få x = 52°. Det betyder att triangelns tredje vinkel måste vara 52°. Den andra vinkeln är 2x (2x 52° eller 104°).

Bild med titeln Hitta den tredje vinkeln i en triangel Steg 8

5. Kontrollera ditt arbete. Om du vill försäkra dig om att detta är en giltig triangel, lägg bara ihop de tre värdena på vinklarna för att se om de summerar till 180°. Det är 52° + 104° + 24° = 180°. Nu är du redo.

Metod 3 av 3: Använd andra metoder

Bild med titeln Hitta den tredje vinkeln i en triangel Steg 9

1. Hitta den tredje vinkeln i en likbent triangel. Likbenta trianglar har två lika sidor och två lika vinklar. De lika sidorna är var och en markerade med ett hash-tecken, vilket indikerar att vinklarna mittemot båda sidorna är lika. Om du känner till vinkelmåttet för en lika vinkel i en likbent triangel, så vet du också den andra lika vinkeln. Du kan bestämma detta enligt följande:

Om en av de lika vinklarna är 40° vet du att den andra vinkeln också är 40°. Du kan hitta den tredje sidan, om det behövs, genom att subtrahera 40° + 40° (det är 80°) från 180°. 180° - 80° = 100°, vilket är den återstående vinkeln.

Bild med titeln Hitta den tredje vinkeln i en triangel Steg 10

2. Hitta den tredje vinkeln i en liksidig triangel. En liksidig triangel har bara lika sidor och lika vinklar. Ofta indikeras detta med två hash-märken i mitten av var och en av sidorna. Det betyder att värdet på valfri vinkel i en liksidig triangel är 60°. Kontrollera ditt arbete. 60° + 60° + 60° = 180°.

Bild med titeln Hitta den tredje vinkeln i en triangel Steg 11

3. Hitta den tredje vinkeln i en rätvinklig triangel. Anta att du har en rätvinklig triangel, vars övriga vinklar är 30°. Om det är en rätvinklig triangel så vet du att en av vinklarna är exakt 90°. Samma principer gäller. Allt du behöver göra är att lägga ihop de vinklar du känner till (30° + 90° = 120°) och subtrahera talet från 180°. Faktum är att 180° - 120° = 60°. Så den tredje vinkeln är 60°.

Varningar

Att göra ett misstag när man adderar och subtraherar skall resultera i ett felaktigt svar. Det är alltid en bra idé att kontrollera ditt arbete, även om det inte verkar vara fel.