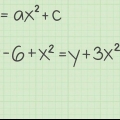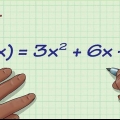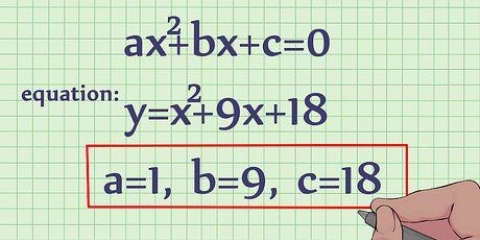Ett polynom utan rötter eller bråk med variabler i nämnaren. Domänen för denna typ av funktion består av mängden av alla reella tal. En funktion med en bråkdel med en variabel i nämnaren. För att hitta domänen för denna typ av funktion, sätt nämnaren för bråket lika med noll och ignorera x-värdet du hittar efter att ha löst ekvationen. En funktion med en variabel inuti en radikal. För att hitta domänen för denna typ av funktion, ställ in termerna inom radikalen större än 0 och lös ekvationen för att ta reda på vilka värden för x som är korrekta inom denna funktion. En funktion med en naturlig logaritm (ln). Gör termerna inom parentes >0 och lös. En graf. Deducera från grafen vilka värden som är korrekta för x. En relation. Detta är en lista över x- och y-koordinater. Din domän är helt enkelt en lista med x-koordinater. 
Strukturen för en domän är en öppen fyrkantig/rund parentes, följt av domänens 2 ändpunkter separerade av ett kommatecken och följt av en avslutande fyrkantig/rund parentes. Till exempel: [-1,5). Det betyder att domänen går från -1 till 5. Använd hakparenteser som [ och ] för att ange om ett nummer faller inom en viss domän. Så i exemplet, [-1,5), faller -1 inom domänen. Använd parenteser som ( och ) för att indikera att ett nummer ligger utanför en viss domän. Så i exemplet, [-1,5), är 5:an utanför domänen. Domänen stannar när som helst före 5:an, till exempel 4 999.. Använd "U" (betyder "union") för att koppla ihop delar av domänen som är separerade från varandra.` Till exempel: [-1,5) U (5,10]. Det betyder att domänen går från -1 till 10, men det finns en lucka i domänen vid 5. Detta kan till exempel bero på en funktion med "x - 5" i nämnaren. du kan göra så mycket "DU"-använd symboler vid behov, om domänen har flera pauser. Använd oändlighetssymbolen (i positiv och negativ riktning) för att indikera att i den riktningen är domänen oändlig. I oändlighet, använd alltid ( ) och inte [ ]. 

f(x) = 2x/(x - 4) x - 4 = 0 (x - 2 )(x + 2) = 0 x ≠ (2, - 2) 
x = alla reella tal utom 2 och -2 

x-7 0 
x 7 
D = [7,∞) 
Kontrollera nu området under -2 (genom t.ex. -3), om detta ger ett resultat som är större än noll. Det är rätt. (-3) - 4 = 5 Kontrollera nu området mellan -2 och 2. Ta till exempel 0. 0 - 4 = -4, så du vet att siffrorna mellan -2 och 2 inte fungerar. Prova nu ett nummer över 2, till exempel +3. 3 - 4 = 5, så siffrorna över 2 fungerar. Skriv ner domänen när du är klar. Så här skriver du ner det här: D = (-∞, -2) U (2, ∞) 

x - 8 > 0 
x - 8 + 8 > 0 + 8 X > 8 
D = (8,∞) 

En rad. Om du ser en linje på grafen som går till oändlighet, kommer så småningom varje x-värde att finnas i parabeln, så domänen är lika med alla reella tal. En vanlig parabel. Om du ser en parabel som pekar uppåt eller nedåt, så består domänen av alla reella tal, eftersom alla tal på x-axeln slutligen ingår i parabeln. En horisontell parabel. Om du har att göra med en parabel med vertex vid (4,0) som sträcker sig oändligt åt höger, då är din domän lika med D = [4,∞) 




Hitta domänen för en funktion
- Steg
- Metod 1 av 6: Lär dig grunderna
- Metod 2 av 6: Hitta domänen för en funktion som innehåller en bråkdel
- Metod 3 av 6: Hitta domänen för en funktion med en kvadratrot
- Metod 4 av 6: Hitta domänen för en funktion med den naturliga logaritmen
- Metod 5 av 6: Hitta domänen för en funktion med hjälp av en graf
- Metod 6 av 6: Bestämma domänen för en funktion med hjälp av en samling/relation
En funktions domän är en samling tal som passar in i den funktionen. Det är med andra ord en samling x-värden som är associerade med en given ekvation. Uppsättningen av y-värden kallas funktionsområde. Om du vill veta hur du hittar domänen för en funktion i olika situationer, följ dessa steg.
Steg
Metod 1 av 6: Lär dig grunderna

1. Lär dig definitionen av en domän. En funktions domän definieras som mängden av alla reella tal som kan fungera som indata till den funktionen. Med andra ord är en domän den kompletta uppsättningen av x-värden som läggs in i en funktion, vilket resulterar i en uppsättning y-värden.

2. Lär dig hur du hittar domänen för olika funktioner. Typen av funktion avgör den bästa metoden för att hitta en domän. Här är grunderna du behöver för följande funktioner:

3. Förstå notationen för en domän. Rätt notation av en domän är lätt att lära sig, men det är viktigt att du gör detta rätt för att inte missa poäng i prov och tentor. Här är några saker du behöver veta för att korrekt skriva domänen för en funktion:
Metod 2 av 6: Hitta domänen för en funktion som innehåller en bråkdel

1. Skriv uppgiften. Anta att du har följande problem:
- f(x) = 2x/(x - 4)

2. För bråk med en variabel i nämnaren sätter du denna variabel lika med noll i en ekvation. Om du vill hitta domänen för en funktion med ett bråk, exkludera alla x-värden som gör nämnaren lika med noll, eftersom du aldrig kan dividera med noll. Så skriv nämnaren som en ekvation och sätt den lika med 0. Så här gör du:

3. Anteckna domänen. Så här gör du:
Metod 3 av 6: Hitta domänen för en funktion med en kvadratrot

1. Skriv uppgiften. Anta att du har följande problem: Y = (x-7)

2. Se till att termerna inom kvadratroten kan vara större än eller lika med 0. Du kan inte ta kvadratroten ur ett negativt tal, men du kan ta kvadratroten ur noll. Observera att detta inte bara gäller kvadratrötter, utan alla jämna rottal. Det gäller inte för udda radikala tal, eftersom det inte är ett problem om det finns ett negativt tal under det radikala tecknet. Här är ett exempel:

3. Isolera variabeln. Nu för att separera x på vänster sida av ekvationen, lägg till 7 på båda sidor av likhetstecknet, så att det efter denna operation kommer att se ut så här:

4. Skriv domänen korrekt. Detta är den korrekta notationen:

5. Hitta domänen för en funktion med kvadratrot om flera lösningar är möjliga. Anta att du har följande funktion: y = 1/√( ̅x -4). Om du tar nämnaren utanför parentesen och gör den lika med noll får du x ≠ (2, - 2). Så här går du tillväga:
Metod 4 av 6: Hitta domänen för en funktion med den naturliga logaritmen

1. Skriv uppgiften. Anta att du har detta:
- f(x) = ln(x-8)

2. Gör termerna inom parentesen större än noll. Den naturliga logaritmen måste vara positiv, så gör termerna inom parentesen större än noll. Här är ett exempel:

3. Lösa. Separera variabeln x genom att lägga till 8 på båda sidor av ekvationen. Här är hur:

4. Anteckna domänen. Visa att domänen för denna ekvation är lika med alla tal större än 8 till oändligt. Här är hur:
Metod 5 av 6: Hitta domänen för en funktion med hjälp av en graf

1. Se diagrammet.

2. Undersök vilka x-värden som hör till grafen. Detta är lättare sagt än gjort, så här är några tips:

3. Bestäm domänen. Bestäm domänen baserat på vilken typ av graf du har. Om du inte är helt säker men du känner till linjens ekvation, skriv in x-koordinaterna i funktionen för att kontrollera.
Metod 6 av 6: Bestämma domänen för en funktion med hjälp av en samling/relation

1. Skriv ner förhållandet. En relation är helt enkelt en serie av x- och y-koordinater. Anta att du har följande koordinater: {(1, 3), (2, 4), (5, 7)}

2. Skriv ner x-koordinaterna. Dessa är: 1, 2, 5.

3. Bestäm domänen. D = {1, 2, 5}

4. Se till att detta förhållande är en funktion. En relation är en funktion om varje gång du anger en numerisk x-koordinat får du samma y-koordinat som ett svar. Så om du sätter en 3:a framför x får du 6 som y-värde, och så vidare. Nästa förhållande är inte en funktion eftersom du får två olika y-värden för varje värde på "X": {(1, 4),(3, 5),(1, 5)}.
Оцените, пожалуйста статью