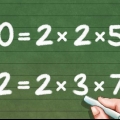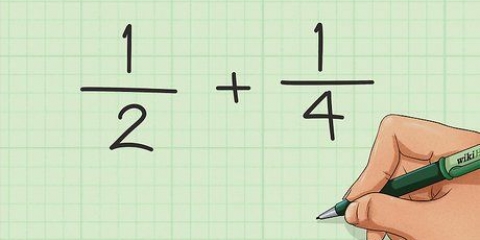Hitta den minsta gemensamma multipeln av två nämnare

Steg
Förnödenheter

Att addera eller subtrahera bråk med olika nämnare. det är nödvändigt att först hitta den minsta gemensamma multipeln av dessa två tal. Detta är den minsta multipeln av någon nämnare i en ekvation. Här är några olika metoder du kan använda för att hitta lcm och använda dem för att lösa bråkproblem.

Steg

Metod 1 av 4: Lista multiplar

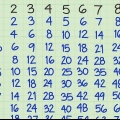
1. Lista multiplar av varje nämnare. Varje lista ska bestå av nämnaren för bråket multiplicerat med 1, 2, 3, 4, och så vidare.

Exempel: 1/2 + 1/3 + 1/5
Multiplar av 2: 2 *1=2; 2 *2=4; 2 *3=6; 2 *4=8; 2 *5=10; 2 *6=12; 2 *7=14; etc.
Multiplar av 3: 3 *1=3; 3 *2=6; 3 *3=9; 3 *4=12; 3 *5=15; 3 *6=18; 3 *7=21; etc.
Multiplar av 5: 5 *1=5; 5 *2=10; 5 *3=15; 5 *4=20; 5 *5=25; 5 *6=30; 5 *7=35; etc.

Bild med titeln Hitta den minsta gemensamma nämnaren Steg 2

2. Hitta den minsta gemensamma multipeln. Skanna igenom varje lista och markera en gemensam multipel av båda nämnarna. Efter att ha bestämt de gemensamma multiplerna, bestäm vilken som är den minsta.

Observera att om det för närvarande inte finns någon gemensam multipel måste du fortsätta tills du hittar en multipel som är giltig för båda nämnarna.

Exempel: 2 *15=30; 3 *10=30; 5 *6=30

kgv=30

Bild med titeln Hitta den minsta gemensamma nämnaren Steg 3

3. Skriv om det ursprungliga problemet. För att skriva varje bråk i denna summa så att det har samma värde som det ursprungliga problemet, är det nödvändigt att multiplicera bråkets täljare och nämnare med lämpligt värde, vilket motsvarar den gemensamma multipeln som hittats.

Exempel: 15 *(1/2); 10 *(1/3); 6 *(1/5)

Ny summa: 15/30 + 10/30 + 6/30

Bild med titeln Hitta den minsta gemensamma nämnaren Steg 4

4. Lösa. Efter att du har hittat LCF och fraktionerna har modifierats bör du kunna lösa detta problem utan problem.

Exempel: 15/30 + 10/30 + 6/30=31/30=1 1/30

Metod 2 av 4: Använd den största gemensamma divisorn

Bild med titeln Hitta den minsta gemensamma nämnaren Steg 5

1. Hitta den största gemensamma delaren för varje nämnare. Ta reda på om det finns en största gemensamma divisor för båda nämnarna genom att ta reda på vilka tal som är delbara med nämnarna.

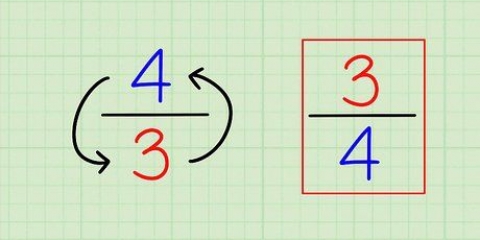
Exempel: 3/8 + 5/12
Faktorer av 8: 1, 2, 4, 8
Faktorer av 12: 1, 2, 3, 4, 6, 12

Bild med titeln Hitta den minsta gemensamma nämnaren Steg 6

2. Identifiera den största gemensamma delaren mellan båda nämnarna. Ringa in alla GCD efter att ha hittat faktorerna för varje nämnare. Den största av GCD:erna är den största gemensamma nämnaren som du kan använda för att ytterligare lösa problemet.

I vårt exempel delar 8 och 12 nämnaren 1, 2 och 4.

Den största gemensamma delaren är 4.

3. Multiplicera nämnarna tillsammans. Gå till nästa steg genom att multiplicera de två nämnarna tillsammans.

Exempel: 8 *12=96

Bild med titeln Hitta den minsta gemensamma nämnaren Steg 7

4. Dela av gcd. När du har hittat produkten av båda nämnarna, dividera denna med den tidigare hittade gcd. Resultatet av denna division är din minsta gemensamma multipel.

Exempel: 96 / 4=24

Bild med titeln Hitta den minsta gemensamma nämnaren Steg 8

5. Skriv om det ursprungliga problemet. Skriv om täljarna genom att multiplicera dem med samma tal som det tog för att göra motsvarande nämnare lika med lcg. Hitta faktorn för varje bråkdel genom att dividera lcm med den ursprungliga nämnaren.

Exempel: 24 / 8=3; 24/12=2

3 *(3/8)=9/24; 2 *(5/12)=10/24

24/9 + 24/10

Bild med titeln Hitta den minsta gemensamma nämnaren Steg 9

6. Lösa problemet. Med den hittade kgv bör det nu vara möjligt att addera och subtrahera utan problem.

Exempel: 9/24 + 10/24=19/24

Metod 3 av 4: Faktorering av fraktioner i primfaktorer

Bild med titeln Hitta den minsta gemensamma nämnaren Steg 10

1. Dela upp nämnare i primtal. Dela upp varje nämnare i en serie primtal. Kom ihåg att primtal är de tal som inte kan delas med något annat tal förutom 1 och sig själv.

Exempel: 1/4 + 1/5 + 1/12
De primära faktorerna för 4: 2 *2
De primära faktorerna för 5: 5
De primära faktorerna för 12: 2 *2 *3

Bild med titeln Hitta den minsta gemensamma nämnaren Steg 11

2. Räkna antalet gånger varje primtal förekommer i uppsättningen primtalsfaktorer. Turf antalet gånger varje primtal förekommer i primtalsfaktorerna för varje nämnare.

Exempel: Det finns två 2-och i 4; noll- 2-och i 5; två 2-och i 12

Det finns noll 3-och i 4 och 5; a 3 i 12

Det finns noll 5-och i 4 och 12; a 5 i 5

Bild med titeln Hitta den minsta gemensamma nämnaren Steg 12

3. Ta det största talet för något primtal. Notera hur många gånger du har använt varje primtal.

Exempel: Det största antalet för 2 är två; det största antalet för 3 är en; det största antalet för 5 är en.

Bild med titeln Hitta den minsta gemensamma nämnaren Steg 13

4. Skriv detta som ett exempel nedan.

Exempel: 2, 2, 3, 5

Bild med titeln Hitta den minsta gemensamma nämnaren Steg 14

5. Multiplicera alla primtal så här. Multiplicera primtalen från föregående serie. Produkten av dessa siffror är lika med lcm för det ursprungliga problemet.

Exempel: 2 *2 *3 *5=60

kgf=60

Bild med titeln Hitta den minsta gemensamma nämnaren Steg 15

6. Skriv om det ursprungliga problemet. Dividera LCF med den ursprungliga nämnaren. Multiplicera varje täljare med samma tal som behövs för att göra motsvarande nämnare till LCF.

Exempel: 60/4=15; 60/5=12; 60/12=5

15 *(1/4)=15/60; 12 *(1/5)=12/60; 5 *(1/12)=5/60

15/60 + 12/60 + 5/60

Bild med titeln Hitta den minsta gemensamma nämnaren Steg 16

7. Lösa. Med den hittade LCF och liknande nämnare har det blivit lätt att addera och subtrahera bråken som vanligt.

Exempel: 15/60 + 12/60 + 5/60=32/60=8/15

Metod 4 av 4: Arbeta med heltal och blandade tal

Bild med titeln Hitta den minsta gemensamma nämnaren Steg 17

1. Konvertera alla heltal och blandade tal till ett oegentligt bråk. Konvertera blandade tal till oegentliga bråk genom att multiplicera heltal före bråket med nämnaren och lägga till täljaren till produkten. Konvertera ett heltal till ett oegentligt bråk genom att placera det som en täljare i ett bråk med nämnaren `1`.

Exempel: 8 + 2 1/4 + 2/3
8=8/1
2 1/4; 2 *4 + 1=8 + 1=9; 9/4
Omskriven uppgift: 8/1 + 9/4 + 2/3

Bild med titeln Hitta den minsta gemensamma nämnaren Steg 18

2. Hitta den minsta gemensamma multipeln av nämnarna. Använd en av metoderna för att hitta LCF för en vanlig bråkdel, enligt beskrivningen ovan. Observera att vi i det här exemplet använder metoden `Listing multipler`, skapar en lista med multiplar för varje nämnare och härleder lcm från detta.

Observera att du inte behöver lista multiplar av 1 eftersom varje tal är en multipel av 1.

Exempel: 4 *1=4; 4 *2=8; 4 *3=12; 4 *4=16; etc.

3 *1=3; 3 *2=6; 3 *3=9; 3 *4=12; etc.

kgv=12

Bild med titeln Hitta den minsta gemensamma nämnaren Steg 19

3. Skriv om det ursprungliga problemet. Istället för att bara multiplicera nämnaren är det nödvändigt att även multiplicera täljaren med det tal som behövs för att göra nämnaren till en lcg.

Exempel: 12 *(8/1)=96/12; 3 *(9/4)=27/12; 4 *(2/3)=8/12

96/12 + 27/12 + 8/12