Använd informationen i uppgiften för att rita beviset. Namnge bekanta och främlingar. När du utarbetar bevisen, använd den nödvändiga informationen för att stödja bevisen. 
Inser du att ett bevis bara är ett bra argument där varje steg är underbyggt. Du kan hitta massor av bevis att studera både online och i en lärobok. 
Rådgör med din lärare efter lektionen för ytterligare förklaring. 

Att känna till din publik hjälper dig att formulera bevisen på ett sätt som den kommer att förstå med tanke på mängden bakgrundskunskap som publiken har. 
Ett tvåkolumnsbevis är en struktur där data och påståenden placeras i en kolumn och stödbeviset bredvid i en andra kolumn. De är mycket vanliga inom geometri. Ett informellt bevis i stycken använder grammatiskt korrekta påståenden och färre symboler. På en högre nivå bör du alltid använda informella bevis. 
Till exempel: Vinkel A och vinkel B bildar ett linjärt par. Utgångspunkt. Vinkel ABC är rak. Rätt vinkel definition. Vinkel ABC är 180°. Definition av en linje. Vinkel A + vinkel B = vinkel ABC. Postulat för att lägga till vinklar. Vinkel A + vinkel B = 180°. utbyte. Vinkel A som ett komplement till vinkel B. Definition av ytterligare vinklar. F.E.d. 
Till exempel: anta att vinkeln A och B är linjära par. Hypotesen är att vinkel A och vinkel B kompletterar varandra (är kompletterande). Vinkel A och vinkel B bildar en rät linje eftersom de är linjära par. En rät linje definieras som en vinkel på 180°. Givet postulatet för addition av vinklar bildar vinklarna A och B tillsammans linjen ABC. Genom substitution är A och B tillsammans 180°, därför är de kompletterande vinklar. F.E.d. 

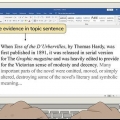
Till exempel: Bevisa att två vinklar som bildar ett linjärt par (vinkel A och vinkel B) är kompletterande. Givet: vinkel A och vinkel B bildar ett linjärt par Bevis: vinkel A är ett komplement till vinkel B. 
Använd inte variabler i ditt bevis som ännu inte är definierade. Till exempel: Variabler är måtten på vinkel A och vinkel B. 
Redigera stegen i början och slutet för att se om de liknar varandra. Använd data, definitioner du har lärt dig och liknande bevis. Ställ dig själv frågor på vägen. `Varför är det så?` och `Finns det något sätt att detta är osant?` är bra frågor för alla påståenden eller påståenden. Glöm inte att skriva stegen i rätt ordning för det slutliga beviset. Till exempel: Om vinkel A och B är kompletterande, måste de vara 180° tillsammans. De två vinklarna bildar tillsammans linjen ABC. Du vet att de bildar en linje på grund av definitionen av linjära par. Eftersom en rät linje är 180° kan du använda substitution för att bevisa att vinkel A och vinkel B summerar till 180°. 
Börja med att ange vilka antaganden du arbetar med. Dela upp dem i enkla och okomplicerade steg så att läsaren inte behöver undra hur ett steg logiskt följer av ett annat. Det är inte ovanligt att man formulerar flera bevis. Fortsätt att arrangera om tills alla steg är i den mest logiska ordningen. Till exempel: börja från början. Vinkel A och vinkel B bildar ett linjärt par. Vinkel ABC är rak. Vinkel ABC är 180°. Vinkel A + vinkel B = vinkel ABC. Vinkel A + vinkel B = 180°. Vinkel A är ett komplement till vinkel B. 
Undantag från användningen av förkortningar är: t.ex. (till exempel) och d.w.z. (det vill säga), men se till att du använder dem på rätt sätt. 
Försöker tillämpa dina bevis på ett fall där det falsk bör vara, och kontrollera om så verkligen är fallet. Om resultatet inte är falskt, ändra beviset så att det är det. Många geometriska bevis skrivs som ett tvåkolumnsbevis, med påståendet och beviset. Ett formellt matematiskt bevis avsett för publicering skrivs som stycke korrekt grammatik. 
F.E.d. står för `quod erat demonstrandum` (latin för `det som måste bevisas`). Om du inte är säker på om ditt bevis är korrekt, skriv bara i några meningar vad din slutsats är och varför den är viktig.
Formulera matematiska bevis
Matematiska bevis kan vara svårt, men med rätt bakgrundskunskap om både matematik och uppbyggnaden av ett bevis kan du säkert formulera dem framgångsrikt. Tyvärr finns det inget snabbt och enkelt sätt att lära sig hur man bygger bevis. Du behöver en solid grund i dina ämneskunskaper för att komma med rätt satser och definitioner för att utveckla ditt bevis logiskt. Genom att läsa exempel och öva dig själv kommer du att kunna bemästra skickligheten i matematiska bevis.
Steg
Metod 1 av 3: Förstå problemet

1. Förstår frågan. Du måste först bestämma exakt vad det är du försöker bevisa. Denna fråga kommer också att fungera som bevisets slutsats. I detta steg kommer du också att definiera de antaganden du kommer att arbeta med. Att identifiera frågan och göra de nödvändiga antagandena ger dig en utgångspunkt för att förstå problemet och utarbeta bevisen.

2. Rita diagram. När man försöker förstå hur ett matematiskt problem fungerar, är det ibland lättast att rita ett diagram över vad som händer. Diagram är särskilt viktiga i geometriska bevis eftersom de låter dig visualisera vad du faktiskt vill bevisa.

3. Studera bevis för relaterade satser. Bevis är svåra att lära sig att komponera, men ett utmärkt sätt att lära sig detta är att studera relaterade satser och hur de bevisades.

4. Fråga frågor. Det är helt normalt att fastna i bevis. Fråga din lärare eller klasskamrater om du inte kan lista ut det. Den senare kan ha liknande frågor och ni kan samarbeta kring frågorna. Bättre att ställa frågor och sedan förstå än att blint vada igenom bevisen.
Metod 2 av 3: Strukturera ett bevis

1. Definiera matematiska bevis. Ett matematiskt bevis är en serie logiska påståenden som stöds av satser och definitioner, som bevisar riktigheten av ett annat matematiskt påstående. Bevis är det enda sättet att veta om ett påstående är matematiskt giltigt.
- Att kunna formulera ett matematiskt bevis indikerar en grundläggande förståelse av själva problemet och alla begrepp som är involverade i problemet.
- Bevis tvingar dig också att se på matematik på ett nytt och spännande sätt. Bara genom att försöka bevisa något får du mer kunskap och förståelse om det, även om dina bevis i slutändan inte verkar rätt.

2. Känn din publik. Innan du skriver ett bevis måste du tänka på publiken du skriver det för och vad de redan vet. Om du skriver korrektur för en publikation kommer du att göra det annorlunda än för en gymnasieklass.

3. Förstå vilken typ av bevis du formulerar. Det finns några olika typer av bevis, och det du väljer beror på din målgrupp och uppdraget. Om du inte är säker på vilken version du ska använda, fråga din lärare om råd. På gymnasiet kan du förväntas formulera beviset i ett specifikt format, till exempel ett formellt bevis med två kolumner.

4. Skriv beviset i två kolumner som en översikt. Att strukturera ett bevis i två kolumner är ett enkelt sätt att organisera dina tankar och överväga problemet. Rita en linje längs mitten av sidan och skriv alla data och påståenden till vänster. Skriv motsvarande definitioner/påståenden till höger, bredvid de data som de stöder.

5. Konvertera beviset i två kolumner till ett informellt bevis. Utgå från beviset i två kolumner, skriv ett informellt bevis som ett stycke utan för många symboler och förkortningar.
Metod 3 av 3: Formulera bevisen

1. Lär dig ordförrådet för matematiska bevis. Det finns vissa påståenden och meningar som du ser om och om igen i ett matematiskt bevis. Det är meningarna du bör känna till och kunna använda när du formulerar dina egna bevis.
- `Om A, då B` betyder att du måste visa att om A är sant måste B också vara sant.
- "A om och bara om B" betyder att du måste bevisa att A och B är både sanna och falska samtidigt. Bevisa både `Om A, då B` och `Om inte A, då inte B`.
- `A endast om B` betyder detsamma som `Om A, då B`, så det används inte ofta. Det är bra att vara medveten om detta när du stöter på det.
- När du förbereder bevisen, undvik att använda "jag" till förmån för "vi".

2. Registrera all data. När man sammanställer ett bevis är det första steget att identifiera och registrera alla uppgifter. Det här är det bästa stället att börja eftersom det hjälper dig att tänka på vad som är känt och vilken information du behöver för att slutföra beviset. Läs problemet och skriv ner varje detalj.

3. Definiera alla variabler. Förutom att skriva data är det användbart att definiera alla variabler. Skriv definitionerna i början av beviset för att undvika förvirring för läsaren. Om variabler inte definieras kan en läsare lätt gå vilse när han försöker förstå dina bevis.

4. Arbeta igenom bevisen baklänges. Det är ofta lättast att tänka baklänges om ett problem. Börja med slutsatsen, vad du försöker bevisa och tänk på de steg som kan leda dig tillbaka till början.

5. Placera dina steg i logisk ordning. Börja beviset från början och arbeta dig fram till slutsatsen. Även om det är bra att tänka på bevisen, genom att börja med slutsatsen och arbeta baklänges, kommer slutsatsen att sätta slutsatsen genom att presentera de faktiska bevisen. Påståendena i bevisningen måste följa av varandra, med belägg för varje påstående, så att det inte finns anledning att tvivla på giltigheten av dina bevis.

6. Undvik att använda pilar och förkortningar i de skriftliga bevisen. När du beskriver planen för ditt bevis kan du använda stenografi och symboler, men när du skriver det slutliga beviset kan symboler, som pilar, förvirra läsaren. Använd ord som "då" eller "så" istället.

7. Stöd alla påståenden med en sats, lag eller definition. Ett bevis är bara så bra som det bevis som används. Du kan inte göra ett påstående utan att underbygga det med en definition. Se andra liknande bevis som exempel.

8. Avsluta det med en slutsats eller Q.E.d. Det sista påståendet om beviset måste vara den hypotes du försökte bevisa. När du har gjort detta påstående, stäng beviset med en sista symbol, som Q.E.d. eller en sluten ruta, för att indikera att beviset är komplett.
Tips
- Alla dina uppgifter måste vara relaterade till ditt slutliga bevis. Om en data inte bidrar med något alls kan du utesluta den.
"Formulera matematiska bevis"
Оцените, пожалуйста статью