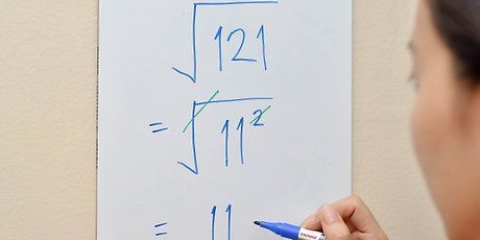Till exempel: om du vill dela upp 20 i faktorer kan du skriva det som 4×5. Observera att variabeltermer också kan skrivas som faktorer. - Till exempel kan 20x skrivas som 4(5x). Primtal kan inte skrivas som faktorer eftersom de bara är delbara med sig själva och 1. 
vafladdermöss mhöja åtta Wrycka till Vmultiplicera delen Oräkna asubtrahera 

Låt oss till exempel hitta liknande termer i vår ekvation 1 + 2x - 3 + 4x. 2x och 4x har båda samma variabel upphöjd till samma potens (i det här fallet har x-variablerna ingen exponent alls). Dessutom är 1 och -3 lika termer, eftersom ingen av dem har en variabel. Så i denna ekvation är 2x och 4x och 1 och-3 lika villkor. 
Vi lägger ihop liknande termer i vårt exempel. 2x + 4x = 6x 1 + -3 = -2 
I vårt exempel var de förenklade termerna 6x och -2, så det nya uttrycket blir 6x - 2. Detta förenklade uttryck motsvarar originalet (1 + 2x - 3 + 4x), men är kortare och lättare att beräkna med. Det är lättare att faktorisera, vilket, som vi kommer att se nedan, är en viktig färdighet att kunna förenkla. 
Anta till exempel att vi har ekvationen 5(3x-1) + x((2x)/(2)) + 8 - 3x. Då skulle det vara felaktigt att omedelbart betrakta 3x och 2x som lika termer och kombinera dem, eftersom parenteserna i uttrycket anger att vi måste göra andra operationer först. Låt oss först utföra de aritmetiska operationerna i uttrycket enligt operationernas ordning, för att få termer som vi har väl kan använda. Se nedan: 5(3x-1) + x((2x)/(2)) + 8 - 3x 15x - 5 + x(x) + 8 - 3x 15x - 5 + x + 8 - 3x. passera nu eftersom de enda operationerna som återstår är addition och subtraktion, kan vi kombinera liknande termer. x + (15x - 3x) + (8 - 5) x + 12x + 3 

Låt oss faktorisera vår ekvation med den största gemensamma divisorn, 3. Det gör vi genom att dividera varje term med 3. 9x/3 = 3x 27x/3 = 9x -3/3 = -1 Så det nya uttrycket är 3x + 9x - 1. 
För vårt exempeluttryck, 3x + 9x - 1, sätter vi uttrycket inom parentes och multiplicerar denna term med den största gemensamma divisorn i den ursprungliga ekvationen för att konvertera 3 (3x + 9x - 1) att få. Denna ekvation motsvarar originalet, 9x + 27x - 3. 
Anta att vårt ursprungliga exempeluttryck, 9x + 27x - 3, är lika med täljaren för en större bråkdel med 3 som nämnare. Denna fraktion ser ut så här: (9x + 27x - 3)/3. Vi kan använda faktorisering för att förenkla denna bråkdel. Lägg till den faktoriserade formen av vårt ursprungliga uttryck till täljaren: (3(3x + 9x - 1))/3 Observera att både täljaren och nämnaren har 3 som koefficient. Om du dividerar täljaren och nämnaren med 3 får du: (3x + 9x - 1)/1. Eftersom en bråkdel med "1" i nämnaren är lika med termerna i täljaren kan vi säga att vårt ursprungliga bråktal kan förenklas till 3x + 9x - 1. 

Låt oss ta ett enkelt exempel - √(90). Om vi tar talet 90 som en produkt av de två faktorerna, 9 och 10, kan vi beräkna kvadratroten ur 9 för att få 3, och sätta den framför radikalen. Med andra ord: (90) √(9×10) (√(9) × √(10)) 3 × √(10) 3√(10) 
Anta till exempel att vi har uttrycket 6x × 8x + (x/x). I alla fall där det är nödvändigt att multiplicera eller dividera exponenter, subtraherar eller adderar vi exponenterna respektive för att snabbt lösa en förenklad term. Se nedan: 6x × 8x + (x/x) (6×8)x + (x) 48x + x För en förklaring, se nedan: Att multiplicera exponentiella termer är i huvudsak detsamma som att multiplicera långa serier av termer utan exponenter. Till exempel eftersom x = x × x × x och x= x × x × x × x × x, x × x = (x × x × x) × (x × x × x × x × x), eller x. På samma sätt är att dividera exponentiella termer detsamma som att dividera långa sekvenser av termer utan exponenter. x/x = (x × x × x × x × x)/(x × x × x). Eftersom vilken term som helst i täljaren kan raderas ut mot samma term i nämnaren, står vi kvar med två gånger ett x i täljaren och inget i nämnaren, vilket lämnar oss med x som svar.
Förenkla matematiska ekvationer
Att kunna förenkla algebraiska ekvationer är en väsentlig del av att bemästra grunderna i algebra och ett extremt värdefullt verktyg för alla matematiker att ha. Förenkling gör det möjligt för en matematiker att ändra ett komplext, långt och/eller klumpigt uttryck till en enklare eller bekvämare men likvärdig form. Grunderna i att förenkla är ganska lätta att lära sig – även för någon som hatar matematik. Genom att följa några enkla steg är det möjligt att förenkla många av de vanligaste algebraiska uttrycken utan några speciella matematiska kunskaper.
Steg
Metod 1 av 4: Förstå nyckelbegrepp

1. Bestämma "lika villkor" enligt deras variabler och krafter. Att äga i algebra "lika villkor" över samma variabler, upphöjda till samma makt. Med andra ord är två termer "liknande", när de har samma variabel(er), eller ingen alls, och när varje variabel har samma styrka, eller ingen. Variablernas ordning inom en term spelar ingen roll.
- Till exempel är 3x och 4x lika termer eftersom varje term har en variabel x upphöjd till andra potens. Variabeln x och x är inte lika termer, eftersom x har olika potens i varje term. Likaså är -3yx och 5xz inte lika termer, eftersom varje term består av olika variabler.

2. Faktorera genom att skriva siffrorna som produkten av två faktorer. Faktorisering är ett sätt att skriva ett givet tal som produkten av två faktorer. Tal kan bestå av flera faktorer – till exempel talet 12, som kan bildas av 1 × 12, 2 × 6 och 3 × 4, så att vi kan säga att 1, 2, 3, 4, 6 och 12 är alla faktorer av 12. Ett annat sätt att se på det är att faktorerna för ett tal är de tal som det är delbart med.

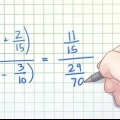
3. Använd minnesminnet "Hur ska vi bli av med otillräckligheterna" (eller som en akronym HMWVDOA) för att komma ihåg ordningen för operationerna. Ibland är att förenkla ett uttryck bara att utföra operationerna i uttrycket tills inget mer kan göras. I så fall är det viktigt att känna till ordningen på operationerna för att undvika räknefel. Detta minnesminne kan hjälpa dig komma ihåg ordningsföljden för redigeringar - bokstäverna motsvarar den typ av redigeringar du behöver utföra och i vilken ordning. Om det finns multiplikationer och divisioner i samma problem, måste du utföra dessa operationer från vänster till höger när du kommer till den punkten. Detsamma gäller för addition och subtraktion. Bilden ovan ger ett svar som inte är korrekt. Det sista steget fungerade inte med addition och subtraktion från vänster till höger. Först lades det till. Det ska vara 25 - 20 = 5 och sedan 5 + 6 = 11.
Metod 2 av 4: Kombinera liknande termer

1. Skriv ner dina ekvationer. De enklaste matematiska ekvationerna (de med bara ett fåtal variabler och koefficienter som heltal, utan bråk, kvadratrötter etc.) kan ofta lösas i några få steg. Som med de flesta matematiska problem, är det första steget för att förenkla en ekvation att skriva ekvationen!
- För nästa steg tar vi uttrycket 1 + 2x - 3 + 4x som ett exempel.

2. Bestäm vilka liknande termer är. Leta nu efter liknande termer i din ekvation. Kom ihåg att lika termer båda har samma variabel(er) och exponent(er).

3. Kombinera liknande termer. Nu när du har bestämt liknande termer kan du börja kombinera dem för att förenkla din ekvation. Lägg till termer tillsammans (eller subtrahera dem i fallet med negativa termer) för att förenkla varje uppsättning termer (med samma variabler och exponenter) till en term.

4. Gör ett förenklat uttryck av dina förenklade termer. Efter att ha kombinerat dina liknande termer, konstruera ett uttryck från din nya, mindre uppsättning termer. Du bör nu ha ett enklare uttryck med en term för varje uppsättning av variabler och exponenter i det ursprungliga uttrycket. Detta nya uttryck motsvarar det första.

5. Följ operationsordningen när du kombinerar liknande termer. I mycket enkla uttryck som de vi behandlade i övningarna ovan är det lätt att känna igen liknande termer. I de mer komplexa uttrycken, som de med termer inom parentes, bråktal och rötter, blir det inte omedelbart uppenbart att kombinera lika termer. I dessa fall följer du operationssekvensen och utför operationerna på termerna i ditt uttryck tills du bara har addition och subtraktion.
Metod 3 av 4: Factoring

1. Hitta den största gemensamma delaren i uttrycket. Factoring är ett sätt att förenkla uttryck genom att ta bort faktorer som förekommer i alla termer av uttrycket. För att börja, hitta den största gemensamma delaren av alla termer i uttrycket - med andra ord, det största antalet som alla termer i uttrycket är delbara med.
- Anta att vi tar ekvationen 9x + 27x - 3. Observera att varje term i denna ekvation är delbar med 3. Eftersom Nej av termerna är helt delbart med ett annat, större antal, det kan vi säga 3 är den största gemensamma nämnaren för vårt uttryck.

2. Dela termerna i uttrycket med den största gemensamma divisorn. Dela sedan varje term i din ekvation med den största gemensamma divisorn du just hittat. De resulterande termerna kommer alla att ha mindre koefficienter än de i det ursprungliga uttrycket.

3. Skriv ditt uttryck som produkten av den största gemensamma delaren och de återstående termerna. Ditt nya uttryck är inte detsamma som det gamla, så det är inte korrekt att säga att det är den förenklade versionen. För att göra det nya uttrycket lika med det gamla måste vi ta hänsyn till att det är dividerat med den största gemensamma divisorn. Sätt ditt nya uttryck inom parentes och skriv den största gemensamma divisorn för den ursprungliga ekvationen som koefficienten för uttrycket också inom parentes.

4. Faktor för att förenkla bråk. Du kanske nu undrar varför faktorisering är användbart om det nya uttrycket måste multipliceras igen efter att ha tagit bort den största gemensamma divisorn. Factoring tillåter en matematiker att använda ett antal knep för att förenkla ett uttryck. Ett av de enklaste av dessa knep använder det faktum att multiplicering av täljaren och nämnaren för ett bråk med samma tal ger ett bråk i samma proportioner. Se nedan:
Metod 4 av 4: Använd förenkla

1. Förenkla bråk genom att dividera med lika faktorer. Som nämnts ovan, om täljaren och nämnaren för ett uttryck har samma faktorer, kan dessa faktorer tas bort från bråket. Ibland kräver detta att täljaren, nämnaren eller båda faktoriseras (som var fallet i exemplet ovan), medan i andra fall de delade faktorerna är omedelbart uppenbara. Observera att det även går att dividera de enskilda termerna i täljaren med uttrycket i nämnaren, för att få ett förenklat uttryck.
- Låt oss ta itu med ett exempel som inte nödvändigtvis kräver att du skriver ut dem för att förenkla. Anta att du har bråket (5x + 10x + 20)/10, du kan dividera varje term i täljaren med 10 i nämnaren, för att förenkla helheten, även om "5" i 5x inte större än 10 och det är inte möjligt att välja 10 som en faktor.
- Genom att göra detta får vi ((5x)/10) + x + 2. Om vi vill kan vi skriva om den första termen som (1/2)x för att få (1/2)x + x + 2.

2. Använd kvadratrötter för att förenkla rötter. Uttryck under tecknet för en kvadratrot kallas kvadratrotsekvationer. Du kan förenkla detta genom att bestämma kvadratrötterna (faktorer som själva bildar en andra potens av ett heltal), varefter du subtraherar kvadratroten av dessa faktorer för att ta bort dem från det radikala tecknet.

3. Lägg ihop exponenterna när du multiplicerar två exponentiella termer och subtrahera dem när du dividerar. Vissa algebraiska ekvationer kräver multiplicering eller division av exponentiella termer. Man räknar inte fram varje exponentiell term och man multiplicerar eller dividerar inte manuellt, men räkna du lägger ihop exponenterna för varje term när du multiplicerar dem och drar du dem när du delar dem, sparar du mycket tid. Du kan också använda detta koncept för att förenkla ekvationer med flera variabler.
Tips
- Kom ihåg att du måste betrakta dessa siffror som positiva eller negativa. Många fastnar i det här och tänker, "Vilken skylt ska jag sätta här?"
- Be om hjälp om du behöver det!
- Att förenkla matematiska ekvationer är inte lätt, men när du väl fått kläm på det kan du använda det resten av ditt liv.
Varningar
- Var försiktig så att du inte av misstag lägger till några extra nummer, exponenter eller operationer som inte hör hemma där.
- Var alltid uppmärksam på lika villkor och låt inte exponenterna lura dig.
"Förenkla matematiska ekvationer"
Оцените, пожалуйста статью