Förenkla matematiska bråk

Steg
Tips
Varningar

Matematiska eller algebraiska bråk verkar oerhört svåra till en början och kan verka skrämmande för den otränade eleven att ta sig an. Med en blandning av variabler, tal och till och med exponenter är det svårt att veta var man ska börja. Men lyckligtvis gäller samma regler som behövs för att förenkla vanliga bråk, som 15/25, också för matematiska bråk.

Steg

Metod 1 av 3: Förenkla fraktioner

1. Känna till ordförrådet för matematiska bråk. Följande termer kommer att användas i exemplen och är vanliga i problem med bråk:

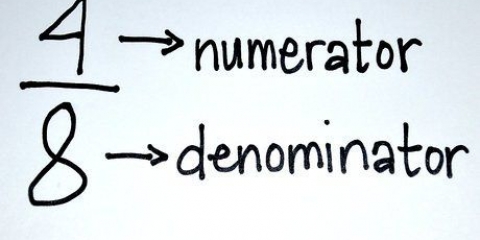
Disken: Den övre delen av en bråkdel (t.ex. (x+5)/(2x+3)).
Nämnare: Den nedre delen av en bråkdel (t.ex. (x+5)/(2x+3)).
Gemensam nämnare: Detta är ett tal med vilket du kan dividera både täljaren och nämnaren för ett bråk. Till exempel, i bråket 3/9 är den gemensamma divisorn 3, eftersom båda talen kan delas med 3.
Faktor:` Ett tal som multipliceras för att göra ett annat tal. Till exempel: faktorerna 15 är 1, 3, 5 och 15. Faktorerna 4 är 1, 2 och 4.
Förenklad ekvation: Alla gemensamma faktorer tas bort och lika variabler grupperas (5x + x = 6x) tills du har fått den enklaste formen av en bråkdel, ekvation eller problem. Om du inte kan göra något med bråket längre är det förenklat.

Bild med titeln Förenkla algebraiska fraktioner Steg 2

2. Jämför hur man löser enkla bråk. Det här är exakt samma steg som du kommer att ta för att lösa matematiska bråk. Ta exemplet, 15/35. För att förenkla en bråkdel behöver vi hitta en gemensam nämnare. I det här fallet kan båda talen delas med fem, så du kan stryka ut 5:an från bråket:
15→5 *3
35→5 *7
Nu kan du stryk ut som termer. I det här fallet kan du stryka över de två femmorna och lämna ditt förenklade svar, 3/7.

Bild med titeln Förenkla algebraiska fraktioner Steg 3

3. Ta bort faktorer från algebraiska uttryck precis som normala tal. I föregående exempel kunde du enkelt ta bort 5:an från 15, och samma princip gäller för mer komplexa uttryck som 15x - 5. Hitta en faktor som båda siffrorna har gemensamt. Här är svaret 5, eftersom du kan dividera både 15x och -5 med siffran fem. Som tidigare tar du bort den gemensamma faktorn och multiplicerar den med vad som är "vänster".`
15x - 5 = 5 *(3x - 1) För att kontrollera ditt arbete, multiplicera bara de fem tillbaka till det nya uttrycket - du kommer att sluta med samma siffror som du började med.

Bild med titeln Förenkla algebraiska fraktioner Steg 4

4. Nu kan du ta bort komplexa termer precis som enkla termer. Samma princip som med vanliga bråk fungerar även för matematiska bråk. Detta är det enklaste sättet att förenkla bråk. Ta bråket:
(x+2)(x-3)
(x+2)(x+10)
Lägg märke till hur termen (x+2) visas i både täljaren (överst) och nämnaren (nederst). Som sådan kan du ta bort dessa för att förenkla den algebraiska bråkdelen, precis som du tog bort 5:an från 15/35:
~~(x+2)~~(x-3)→(x-3)
~~(x+2)~~(x+10)→(x+10) Detta ger det slutliga svaret: (x-3)/(x+10).

Metod 2 av 3: Förenkla fraktioner

Bild med titeln Förenkla algebraiska fraktioner Steg 5

1. Hitta en gemensam faktor i täljaren (den övre delen av bråket). Det första du ska göra när du förenklar en algebraisk bråkdel är att förenkla varje del av bråket. Börja med den övre delen och stryk över så många siffror som möjligt. Som ett exempel kommer vi att använda den här övningen:
9x-3
15x+6
Börja med räknaren: 9x – 3. Det finns en gemensam faktor för både 9x och -3, vilket är 3. Arbeta med de 3 yttre fästena som du skulle göra med alla andra siffror, lämna 3*(3x-1). Det här är din nya räknare:
3(3x-1)
15x+6

Bild med titeln Förenkla algebraiska fraktioner Steg 6

2. Hitta en gemensam faktor i nämnaren.Fortsätt exemplet ovanifrån, isolera nämnaren, 15x+6. Sök igen efter ett nummer som passar båda delarna. Även här kan du utelämna en faktor tre, så att du står kvar med 3 *(5x +2). Inkludera din nya nämnare i ekvationen:
3(3x-1)
3(5x+2)

Bild med titeln Förenkla algebraiska fraktioner Steg 7

3. Ta bort liknande termer. Detta är steget där du verkligen kan förenkla bråket. Ta alla termer som finns i både täljaren och nämnaren och ta bort dem. I det här fallet kan vi stryka ut 3 från både toppen och botten.
3(3x-1)→(3x-1)
3(5x+2)→(5x+2)

Bild med titeln Förenkla algebraiska fraktioner Steg 8

4. Vet när ekvationen är helt förenklad. En bråkdel förenklas när det inte finns fler vanliga faktorer i toppen eller botten. Kom ihåg att du inte kan ta bort faktorer från parentesen - i exemplet kan du inte faktorisera x-värdet för 3x och 5x, eftersom de fullständiga termerna faktiskt är (3x -1) och (5x + 2). Så exemplet är helt förenklat, med if det sista svaret:
(3x-1)
(5x+2)

Bild med titeln Förenkla algebraiska fraktioner Steg 9

5. Prova en övningsövning. Det bästa sättet att lära sig är att fortsätta att försöka förenkla matematiska bråk. Svaren finns under problemen.
4(x+2)(x-13)
(4x+8)Svar: (x=13)
2x-x
5xSvar:(2x-1)/5

Metod 3 av 3: Knep för att lösa svårare problem

Bild med titeln Förenkla algebraiska fraktioner Steg 10

1. `Invertera` bråk för att faktorisera med negativa tal. Låt oss säga att vi har följande ekvation:
3(x-4)
5(4-x)
Notera hur (x-4) och (4-x) nästan är identiska, men du kan inte stryka över dem eftersom de är omvända. Däremot kan (x - 4) skrivas som -1 *(4 - x) på samma sätt som du skriver om (4 + 2x) som 2 *(2 + x). Detta kallas "föra utanför parentesen".
-1 *3(4-x)
5(4-x)
Nu kan vi helt enkelt utelämna de två identiska (4-x):
-1 *3~~(4-x)~~
5~~(4-x)~~
Av detta följer det slutliga svaret: -3/5

Bild med titeln Förenkla algebraiska fraktioner Steg 11

2. Upptäck skillnaden mellan två rutor medan du arbetar. Skillnaden mellan två kvadrater är helt enkelt att subtrahera ett kvadratiskt tal från ett annat, som uttrycket (a - b). Skillnaden mellan perfekta kvadrater förenklas alltid i två delar, genom att addera och subtrahera kvadratrötterna. I vilket fall som helst kan du förenkla skillnaden mellan perfekta rutor så här:
a - b = (a+b)(a-b) Detta kan vara till stor hjälp när du försöker hitta liknande termer i matematiska bråk.

Exempel: x - 25 = (x+5)(x-5)

Bild med titeln Förenkla algebraiska fraktioner Steg 12

3. förenkla polynom. Polynom eller polynom är komplexa algebraiska uttryck med fler än två termer, till exempel: x + 4x + 3. Lyckligtvis kan många polynom förenklas genom att "faktorisera". Det föregående uttrycket kan till exempel skrivas om som (x+3)(x+1).

Bild med titeln Förenkla algebraiska fraktioner Steg 13

4. Kom ihåg att variabler också kan faktoriseras. Detta är särskilt användbart för uttryck med exponenter, som x + x. Du kan utelämna den största exponenten som en faktor. I det här fallet: x + x = x(x + 1).

Tips

Kontrollera ditt arbete med factoring genom att multiplicera faktorn tillbaka i ekvationen - du får samma tal som du började med.
Ta alltid bort de största siffrorna du kan för att helt förenkla din ekvation.