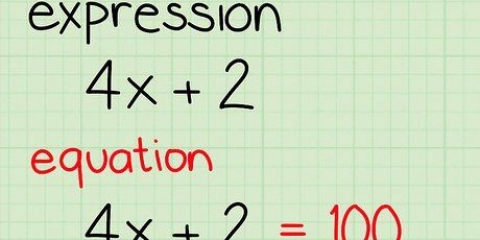Exempel: följande uttryck 2x + 4(5 + 2) + 3 - (3 + 4/2). Lös först termerna inom parentes, så 5 + 2 och 3 + 4/2. 5 + 2 = 7. 3 + 4/2 = 3 + 2 = 5. Termen mellan det andra paret av parenteser blir 5 eftersom vi först måste räkna ut 4/2 och först därefter räkna ut additionen. Om vi helt enkelt skulle arbeta från vänster till höger, så skulle summan vara 3 + 4 : 2, varvid först 3 + 4 och sedan 7/2 skulle beräknas, vilket resulterar i fel svar 7/2. Obs – om flera parenteser är kapslade (parenteser inom parentes), lös upp den inre först och arbeta mot de yttre parenteserna. 
Efter att ha löst parenteserna såg exemplet ut så här. 2x + 4(7) + 3 - 5. Den enda makten i vårt exempel är 3, och detta är lika med 9. Uttrycket blir nu 2x + 4(7) + 9 - 5. 
Det finns två multiplikationer i problemet: 2x (2x är 2 × x) och 4(7). Vi vet inte värdet på x, så låt oss lämna det som 2x. 4(7) = 4 × 7 = 28. Vi kan skriva detta annorlunda som 2x + 28 + 9 - 5. 
Eftersom vi redan löst ett divisionsproblem som stod inom parentes finns det inga divisionsproblem kvar i vårt problem, så vi kan hoppa över detta steg. Detta tar upp en viktig punkt - om en operation inte förekommer i ett uttryck, fortsätt sedan till nästa operation som anges i matematikreglerna. 
Vårt uttryck är nu delvis förenklat till "2x + 28 + 9 - 5". Nu lägger vi ihop så mycket som möjligt – från vänster till höger. Vi kan inte lägga till 2x till de andra talen eftersom vi inte vet värdet på x, så vi hoppar över det här. 28 + 9 = 37, så vi kan skriva om uttrycket som "2x + 37 - 5". 
I vårt uttryck, "2x + 37 - 5", det finns bara en subtraktion,37 - 5 = 32 
Vårt sista svar är "2x + 32". Vi kan inte lösa additionen utan att veta värdet av x, men när vi väl gör det är det mycket lättare att lösa än det ursprungliga uttrycket. 

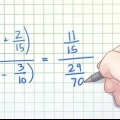
Anta till exempel att vi måste lösa bråket 36/60. Om vi har en miniräknare till hands räknas svaret (6) ut så här. Om vi inte har detta kan vi komma långt genom att eliminera liknande faktorer. Ett annat sätt att tänka på 36/60 är som (6 × 6)/(6 × 10). Detta kan återigen skrivas om till 6/6 × 6/10. 6/6 = 1, så vårt uttryck blir 1 × 6/10 = 6/10. Men vi är inte där än – både 6 och 10 har samma faktor 2. Genom att upprepa ovanstående procedur behåller vi3/5 handla om. 
Anta att vi har uttrycket (3x + 3x)/(-3x + 15x).Detta bråk kan skrivas om som (x + 1)(3x)/(3x)(5 - x), 3x förekommer i både täljaren och nämnaren. Att ta bort dessa faktorer från ekvationen ger (x + 1)/(5 - x). På samma sätt är detta fallet med ekvationen (2x + 4x + 6)/2. Eftersom varje term är delbar med 2 kan vi skriva om den som (2(x + 2x + 3))/2 och därmed förenkla till x + 2x + 3. Tänk på att du inte kan eliminera varje term - bara de faktorer som finns i både täljaren och nämnaren. Till exempel uttrycket (x(x + 2))/x, där "X" kan tas bort från fraktionen och lämnar (x + 2)/1 = (x + 2). Men (x + 2)/x är inte för att förenkla till 2/1 = 2. 
Till exempel kan uttrycket 3(x + 8 förenklas till3x + 24, medan 3x(x + 8) kan förenklas till 3x + 24x. Observera att i vissa fall, som med variabla bråk, kan konstanten utanför parentesen användas i förenklingen och bör därför inte multipliceras. Till exempel, i bråket (3(x + 8))/3x, förekommer faktorn 3 i både täljaren och nämnaren, så vi kan ta bort det och förenkla uttrycket till (x + 8)/x. Detta är enklare och lättare att arbeta med än med (3x + 24x)/3x, vilket skulle ha varit svaret om vi hade multiplicerat. 
Ta en ny titt på uttrycket x - 5x + 6. Detta kan lösas till (x - 3) (x - 2). Så om x - 5x + 6 är täljaren i en ekvation med en av dessa faktorer i nämnaren (som i (x - 5x + 6)/(2(x - 2))), så kan vi faktorisera den i faktorer som t.ex. att vi kan bli av med nämnaren. Med andra ord, vid (x - 3)(x - 2)/(2(x - 2)), (x - 2) faller ut och lämnar oss(x - 3)/2 kvar. Som nämnts ovan kan du också lösa en ekvation med faktorisering, speciellt om den är lika med noll. Till exempel: ta ekvationen x - 5x + 6 = 0. Factoring ger oss (x - 3)(x - 2) = 0. Eftersom ett tal gånger noll är lika med noll, kan vi sätta båda termerna lika med noll för att hitta svaret på detta problem. Så svaret på ekvationen är x=3 och x= 2.
Förenkla matematiska uttryck
Matematikproblem ber ofta om ett svar "så enkelt som möjligt" att skriva ner — med andra ord att ge ett så elegant svar som möjligt. Medan ett långt, klumpigt uttryck och en kortare, mer elegant version av det tekniskt sett betyder samma sak, accepteras ett svar ofta inte förrän det har förenklats så långt som möjligt.Dessutom är förenklade svar också lättare att arbeta med. `Det är därför att lära sig förenkla är en viktig färdighet för framtida matematiker.
Steg
Metod 1 av 2: Ordningen för matematiska operationer

1. Ordningen på operationerna. När du förenklar matematiska uttryck kan du inte bara utvärdera från vänster till höger. Vissa operationer har företräde framför andra och måste därför göras först. Om du inte gör detta kan du få fel svar. Operationsordningen i matematik är följande: Parenteser, Exponentiering och rotning, Multiplikation och division, Addition och Subtraktion. Ett minnesmärke för att komma ihåg denna sekvens är "Hur ska vi bli av med det otillräckliga " eller "HMWVDOA".
- Observera att även om en grundläggande kunskap om operationerna är tillräcklig för att lösa de flesta standarduttryck, behövs speciella tekniker för att lösa uttryck som innehåller variabler, inklusive de flesta polynom. Se metod två för mer information.

2. Börja med att lösa alla termer inom parentes. I matematik betyder parentes att alla termer de omsluter måste lösas separat från det omgivande uttrycket. Oavsett operationer, se till att lösa alla termer inom parentes först om du vill förenkla ett uttryck. Tänk på att beräkningsreglerna för operationsordningen även gäller inom parentes. Så även här först parentes, sedan exponentiering, etc.

3. Lös nu upp befogenheterna. Efter att ha räknat ut parenteserna kan du nu gå vidare till exponentiering. Lös dem en efter en.

4. Lös nu multiplikationssummorna. Kom ihåg att en multiplikation kan skrivas på flera sätt. Med en punkt, utan en punkt eller med en ×-symbol. Men också något liknande 4(x)) indikerar en multiplikation.

5. Fortsätt med divisionsproblem. Om du letar efter divisionsproblem, kom ihåg att även dessa kan skrivas på olika sätt. Den enkla ÷-symbolen , med ett kolon eller ett snedstreck (som t.ex 3/4) alla indikerar en division.

6. Lägg till. Lägg nu ihop de olika termerna. Arbeta ut detta från vänster till höger, som det är i uttrycket och vilket som är lämpligast. Till exempel, i summan 49 + 29 + 51 +71 är det lättare att dela upp problemet i följande block: 49 + 51 = 100, 29 + 71 = 100 och 100 + 100 = 200. Detta är lättare än 49 + 29 = 78, 78 + 51 = 129 och 129 + 71 = 200.

7. subtrahera. Det sista steget i operationerna är att subtrahera de återstående termerna. Träna ut resten av ditt uttryck, från vänster till höger. Du kan lägga till negativa tal i detta eller föregående steg - det spelar ingen roll för ditt svar.

8. Se ditt uttryck. Efter att ha arbetat igenom operationssekvensen står du kvar med ett antal termer i den mest förenklade formen. Om det finns en eller flera variabler i uttrycket förblir de i stort sett oförändrade. Att förenkla uttryck med variabler kräver att vi löser dessa ekvationer ytterligare för okända, eller med hjälp av speciella metoder (se nästa steg).
Metod 2 av 2: Förenkla komplexa uttryck

1. Lägg till lika stora potenser. När man har att göra med uttryck som innehåller variabler är det viktigt att komma ihåg att termer med samma variabel och samma exponent (eller "lika villkor") kan adderas (eller subtraheras) som vanliga tal. Villkoren måste har inte bara samma variabel, utan också samma exponent. Till exempel kan 7x och 5x läggas ihop, men 7x och 5x kan inte.
- Denna regel kan också utökas till multivariata termer. Till exempel kan 2xy läggas till -3xy, men inte -3xy eller -3y.
- Ta följande uttryck:x + 3x + 6 - 8x. I det här uttrycket kan vi lägga till termerna 3x och -8x eftersom de är lika med varandra. Vårt uttryck blir då förenklat: x - 5x + 6.

2. Förenkla bråk genom att eliminera eller dividera faktorer. Bråk som bara består av tal (och inga variabler) kan förenklas på flera sätt. Ett bråk är bara en divisionssumma och bör behandlas som sådan. Dessutom, om samma multiplikation förekommer i täljaren eller nämnaren, kan den elimineras, eftersom de redan ger svar 1 när de delas. Med andra ord, om täljaren och nämnaren båda har samma faktor, kan de tas bort från bråket, vilket förenklar resultatet.

3. Om du har att göra med bråk som innehåller variabler, försök att eliminera variablerna. Dessa uttryck erbjuder unika möjligheter att förenkla. Precis som vanliga bråk, låter variabla bråk dig ta bort faktorer som finns i både täljaren och nämnaren. Men i det senare fallet kan dessa faktorer vara såväl siffror som variabler.

4. Multiplicera termerna inom parentes med deras konstanter. När man har att göra med variabla termer inom parentes plus en konstant, kan multiplicera en term inom parentesen med konstanten utanför parentesen resultera i ett enklare uttryck.Det gäller både numeriska konstanter och konstanter med variabler.

5. Förenkla genom att faktorisera. Detta är en teknik som kan förenkla vissa ekvationer. När du factoring, tänk på något som är motsatsen till "multiplicera parenteser" – ibland kan en ekvation representeras enklare som två termer multiplicerade än som en ekvation. Detta gäller särskilt om du kan eliminera en del av ekvationen med den. I vissa fall (som med andragradsekvationer) kan man också lösa själva ekvationen med faktorisering.
"Förenkla matematiska uttryck"
Оцените, пожалуйста статью