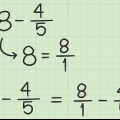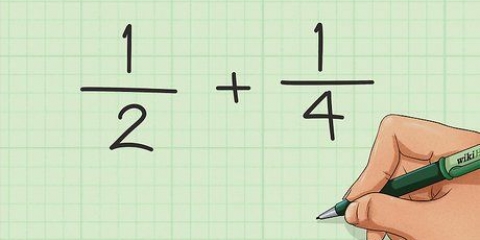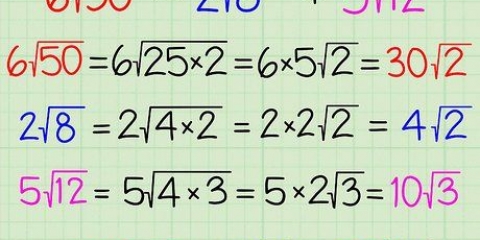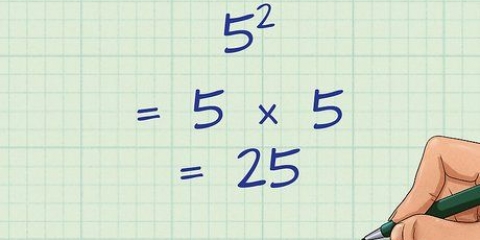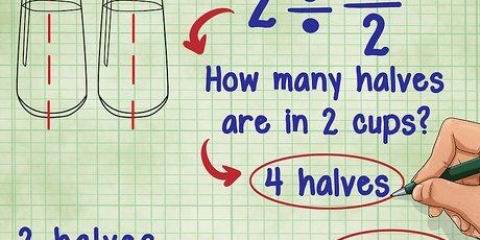Oavsett om du skriver 1/5 + 2/5 eller 1+2/5 är svaret detsamma: 3! Slutligen, 1 + 2 = 3. 
Så, efter samma exempel, är nämnaren 5. Det är allt! Detta är det nedersta numret på bråkdelen och hälften av svaret! 
Vad var disken? 3. Och nämnaren? 5. Så, 1/5 + 2/5, eller 1+2/5, är lika med 3/5. 

Så 2/3 blir 2/3 x 4 och 3/4 blir 3/4 x 3. Det betyder att vi nu har 2/12 och 3/12. Men vi är inte klara än! Du kommer att märka att i det här fallet har nämnarna multiplicerats med varandra. Detta fungerar i den här situationen, men inte alltid. Ibland måste du leta efter mindre tal för att hitta LCF. Och i andra fall, med små tal, är allt du behöver göra att multiplicera nämnarna tillsammans. 
Vi hade 2/3x4 och 3/4x3 som vårt första steg - för att lägga till det andra steget är det faktiskt 2 x 4/3 x 4 och 3 x 3/4 x 3. Det betyder att 8/12 och 9/12 är våra nya nummer. Perfekt! 
I det här exemplet gäller: 8+9/12 = 17/12. För att konvertera detta till ett blandat tal, subtrahera nämnaren från täljaren och se vad du har kvar med. Det vill säga i det här fallet 17/12 = 1 5/12 

Låt oss avgöra vad som är multiplerna av 12 och 8. Vilket är det minsta talet som båda talen passar in i?? 24. 8, 16, 24 och 12, 24 – bingo! 
Alltså 13 x 2/12 x 2 = 26/24. Och 17 x 3/8 x 3 = 51/24. Vi har kommit långt för att lösa problemet! 
26/24 + 51/24 = 77/24. Det var den paus du letade efter! Men disken är ganska stor.... 
För det här exemplet: 24 går in i 77 3 gånger.Så, 24 x 3 = 72. Sedan återstår en rest av 5! Så vad är ditt slutliga svar? 3 5/24. Det är allt!
Addera och subtrahera bråk
Att lägga till och subtrahera bråk är en viktig färdighet att lära sig. Man stöter på bråk överallt i vardagen, särskilt i mattelektionen, från grundskolan till universitetet. Följ bara stegen nedan för att lära dig hur du adderar och subtraherar bråk oavsett om de är lika, ojämna, blandade eller oegentliga bråk. När du väl har lärt dig på ett sätt är allt annat mycket enklare!
Steg
Metod 1 av 3: Addera och subtrahera bråk med samma nämnare

1. Skriv ekvationen. Om nämnaren för de två bråken du adderar/subtraherar är densamma, inkludera även denna nämnare i ditt svar.
- Du behöver med andra ord inte skriva 1/5 och 2/5 som 1/5 + 2/5 = ? Detta kan noteras som (1+2)/5 = ?. Nämnaren är densamma och behöver därför bara nämnas en gång. Båda täljarna är ovanför poänglinjen.

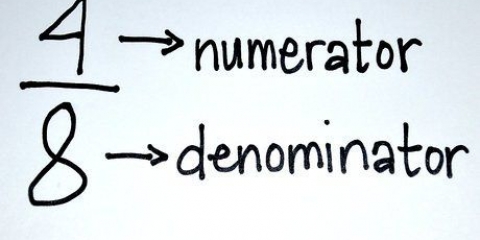
2. Lägg ihop räknarna. Täljaren är talet ovanför bråklinjen. Ta följande exempel: 1/5 och 2/5; här är 1 och 2 våra räknare.

3. Lämna nämnaren oförändrad. Inget att lägga till, subtrahera, etc, men oförändrat.

4. Skriv ner svaret. Nu är det bara att skriva svaret! Du kommer att se att enligt föregående exempel är svaret 3/5.
Metod 2 av 3: Addera och subtrahera bråk med olika nämnare

1. Hitta minsta gemensamma multipel (LCM) av nämnarna. Detta är det minsta antal som båda nämnarna har gemensamt. Ta bråken 2/3 och 3/4. Vilka är nämnarna? 3 och 4. För att hitta LCF för båda, använd ett av följande tre sätt:
- Skriv ner multiplerna. Multiplerna av 3 är 3, 6, 9, 12, 15, 18...och så vidare. Multiplarna av 4? 4, 8, 12, 16, 20 osv. Vilket är det lägsta antalet som förekommer i båda uppsättningarna?? 12! Det är din minsta gemensamma multipel eller din kgv.
- Faktorisering i primtalsfaktorer. Om du vet vad primfaktorer är kan du använda faktorisering. Här bestämmer du med vilka primtal du kan multiplicera ett visst tal med hjälp av multiplikation "att göra". För 3 är faktorerna 3 och 1. För 4 är primfaktorerna 2 och 2. Sedan multiplicerar du dessa tillsammans, så 3 x 2 x 2 = 12. din kgf!
- Multiplicera båda siffrorna tillsammans för att fåliten tal. I vissa fall, som det här, kan du bara multiplicera båda talen tillsammans – 3 x 4 = 12. Men om dina nämnare är stora siffror kan detta inte bara hända! Du kan inte bara göra 56 x 44 och gå vidare till 2464 som ett svar! Det är inte fel, men det är besvärligt.

2. multiplicera nämnaren med talet du behöver för att få lcg. Med andra ord vill du att varje nämnare ska vara samma tal – kgv. För vårt exempel måste detta vara 12. 4 x 3 = 12. Detta är nämnaren i vårt slutliga svar.

3. Multiplicera täljaren med det numret också. Om du multiplicerar nämnaren för ett bråk med ett tal, måste du också multiplicera täljaren med samma tal. Det vi gjorde i det sista steget var bara en del av den nödvändiga multiplikationen.

4. Lägg till (eller subtrahera) täljarna för att få ditt svar. För att lägga till 8/12 till 9/12, lägg bara ihop täljarna. Glöm inte: du lämnar nämnaren ifred. Siffran du fick med LCF är din slutliga nämnare.
Metod 3 av 3: Addera och subtrahera blandade och oegentliga fraktioner

1. Konvertera dina blandade bråk till oegentliga bråk. En blandad bråkdel är ett heltal med en bråkdel efter, som i exemplet ovan (1 5/12). Ett oegentligt bråk är ett bråk med en större täljare än nämnaren. Ett exempel på detta är 17/12.
- Som exempel tar vi 13/12 och 17/8.

2. Hitta den gemensamma nämnaren. Kom ihåg de tre sätten att hitta nämnarnas lcg? Genom att bestämma multiplerna, använda primtalsfaktorer eller genom att multiplicera nämnarna tillsammans.

3. Multiplicera täljarna med nämnarna för att få lika bråkdel. Båda nämnarna måste nu omvandlas till 24. Hur man gör 24 av 12? Multiplicera det med 2. Från 8 till 24? Multiplicera det med 3. Men glöm inte att du också måste multiplicera täljarna!

4. Addera och subtrahera bråk. Nu när båda bråken har samma nämnare kan du enkelt addera eller subtrahera båda bråken. Kom ihåg, lämna nämnaren ifred!

5. Gör ditt svar till en blandad bråkdel. En så stor täljare är lite märklig och gör det svårt att få en uppfattning om storleken på din bråkdel. Allt du behöver göra för att lösa det är att dividera täljaren med nämnaren och använda resten som täljare för din nya sammansatta bråkdel.
"Addera och subtrahera bråk"
Оцените, пожалуйста статью