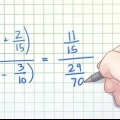
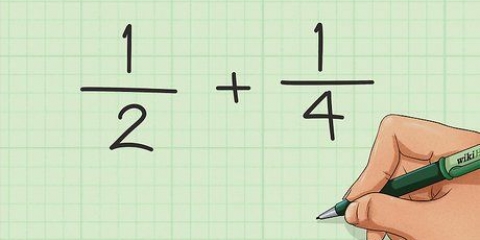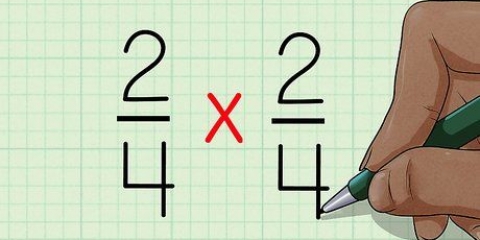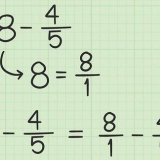(/2) = /2 × /2 eller (/2). Att kvadrera varje nummer ger (/4). 
Täljaren stannar överst på bråket och nämnaren stannar på botten. Till exempel: (/2) = (/2 x 2) = (/4). 
För att konvertera detta till ett blandat tal, dividera 25 med 4. Detta är 6 (6 x 4 = 24), med en återstod av 1. Därför är det blandade talet 6/4. 

Till exempel: (-/4) = (–/4) x (–/4) 
Till exempel: (-2) x (-8) = (+16) 
Om du fortsätter med exemplet kommer det resulterande bråket att vara ett positivt tal. (–/4) x (–/4) = (+/16) Bruket är att utelämna plustecknet från positiva tal. 
Till exempel: (/16) har en gemensam faktor fyra. Dividera bråket med 4: 4/4 = 1, 16/4= 4 Skriv om det förenklade bråket: (/4) 

Till exempel: 16 × (/16) Kvadra parenteserna och ta bort den gemensamma faktorn 16: 16 * /16 * /16 Eftersom du här har att göra med en 16 som ett heltal och två gånger en 16 i nämnaren, kan du eliminera en av dem. Skriv om den förenklade ekvationen: 12 × /16 förenkla /16 genom att dividera med 4: /4 Multiplicera: 12 × /4 = 36/4 Del: 36/4 = 9 
Till exempel: 16 * (/16) Skriv om med kvadratisk täljare och nämnare: 16 * (/16) Subtrahera exponenten i nämnaren: 16 * /16 Föreställ dig de första 16 som en exponent för 1:16. Med hjälp av reglerna för att subtrahera potenser/exponenter subtraherar man exponenterna från varandra. 16/16, ger 16 = 16 eller 1/16. Nu fortsätter du med /16 Skriv om och förenkla bråket: /16 =* /4. Förenkla: 12 × /4 = 36/4 Del: 36/4 = 9
Kvadrera bråk
Att kvadrera bråk är en av de enklaste operationerna du kan utföra på bråk. Det är väldigt likt att kvadrera heltal genom att du bara kan multiplicera både täljaren och nämnaren med sig själva. Det finns vissa fall där förenkling av fraktionen före kvadrering gör proceduren enklare. Om du ännu inte har lärt dig den här färdigheten ger den här artikeln en kort översikt för att förbättra din förståelse.
Steg
Del 1 av 3: Kvadrering av bråk

1. Förstå hur man kvadrerar heltal. När du ser ett tal upphöjt till andra potens vet du att talet ska kvadrat. Detta är samma sak som att multiplicera talet med sig själv. Till exempel:
- 5 = 5 × 5 = 25

2. Inser du att kvadreringenfraktioner fungerar på samma sätt. För att kvadrera ett bråk, multiplicera bråket med sig självt. Ett annat sätt att tänka på detta är att multiplicera täljaren med sig själv och nämnaren med sig själv. Till exempel:

3. Multiplicera täljaren med sig själv och nämnaren med sig själv. Den faktiska ordningen i vilken du multiplicerar dessa siffror med sig själva spelar ingen roll, så länge du kvadrerar båda talen. För att göra det enkelt, börja med täljaren: multiplicera den med sig själv. Multiplicera sedan nämnaren med sig själv.

4.Förenkla bråkdelen för att avsluta detta. När det gäller bråk är det sista steget alltid att förenkla bråket till sin enklaste form eller omvandla ett oegentligt bråk till ett blandat tal. Vårt exempel, /4 är ett oegentligt bråk eftersom täljaren är större än nämnaren.
Del 2 av 3: Kvaddra bråk med negativa tal

1. Leta efter ett minustecken framför bråket. Om du har att göra med en negativ bråkdel finns det ett minustecken framför det. Det är klokt att alltid sätta parentes runt ett negativt tal så att du vet att minustecknet refererar till talet och inte är tänkt som en minussumma.
- Till exempel: (-/4)

2. Multiplicera bråket med sig själv. Kvaddra bråket som du normalt skulle göra, genom att multiplicera täljaren med sig själv och sedan multiplicera nämnaren med sig själv. Du kan också bara multiplicera bråket med sig själv.

3. Förstå att multiplicera två negativa tal tillsammans ger ett positivt tal. När ett minustecken finns, blir hela bråket negativt. När du kvadrerar bråket multiplicerar du två negativa tal. När två negativa tal multipliceras med varandra är produkten alltid positiv.

4. Ta bort minustecknet efter kvadraten. Om du har kvadrerat bråket har du multiplicerat två negativa tal. Det betyder att den kvadratiska bråkdelen är positiv. Glöm inte att utelämna minustecknet i det slutliga svaret.

5. Förenkla bråket så långt som möjligt. Det sista steget i att göra bråkberäkningar är att förenkla. Oegentliga bråk måste först förenklas till blandade tal och sedan ytterligare förenklas.
Del 3 av 3: Använda förenklingar och snabba lösningar

1. Kontrollera om du kan göra bråketförenkla innan du kvadrerar det. Det är vanligtvis lättare att förenkla bråk före kvadrering. Kom ihåg att för att förenkla ett bråk innebär det att dividera det med en gemensam faktor tills 1 är det enda tal som finns kvar som kan delas med både täljaren och nämnaren. Att förenkla ett bråk först betyder att du inte behöver förenkla det igen i slutet, när siffrorna är större.
- Till exempel: (/16)
- 12 och 16 kan båda delas med 4. 12/4 = 3 och 16/4 = 4; så du kan/16 förenkla till /4.
- Nu kan du göra bråket /4 till kvadrat.
- (/4) = /16, som du inte kan förenkla längre.
- För att bevisa detta kvadrerar vi den ursprungliga bråkdelen utan att förenkla:
- (/16) = (/16x16) = (/256)
- (/256) har en gemensam faktor på 16. Att dividera både täljaren och nämnaren med 16 förenklar bråkdelen till (/16), samma bråkdel som vi fick genom att förenkla först.

2. Lär dig när du ska vänta med att förenkla en bråkdel. Har du att göra med mer komplexa ekvationer, då kan det vara möjligt att eliminera en av faktorerna. I ett sådant fall är det därför bekvämare att vänta med att förenkla fraktionen. Att lägga till en extra faktor till exemplet ovan gör detta tydligare.

3. Förstå hur du gör detta snabbt medexponent. Ett annat sätt att lösa samma problem är att först förenkla exponenten. Resultatet blir detsamma, endast erhålls via en annan väg.
Förnödenheter
- Papper eller en dator
- Penna/penna (om du använder papper)
Оцените, пожалуйста статью