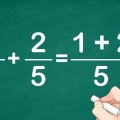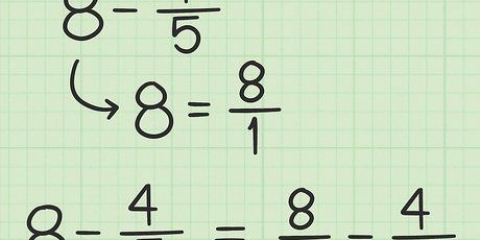Lägg till och subtrahera kvadratrötter: 9 steg (med bilder)

Steg
- Del 1 av 2: Bemästra grunderna
- Del 2 av 2: Mer träning
Tips
Varningar

För att lägga till och subtrahera kvadratrötter måste du kombinera kvadratrötter med samma rot. Det betyder att du kan lägga till (eller subtrahera från) 2√3 till 4√3, men du kan inte lägga till 2√3 och 2√5. Det finns många tillfällen där du kan förenkla talet under radikalen för att kunna kombinera liknande termer och addera och subtrahera kvadratrötter fritt.

Steg

Del 1 av 2: Bemästra grunderna

1. Förenkla termerna under radikalerna om möjligt. För att förenkla termerna under radikalerna, försök att räkna in dem i minst en perfekt kvadrat, till exempel 25 (5 x 5) eller 9 (3 x 3). När du har gjort detta kan du ta kvadratroten av den perfekta kvadraten och placera den utanför radikalerna, och lämna kvarvarande faktor under radikalen. I det här exemplet utgår vi från problemet 6√50 - 2√8 + 5√12. Siffrorna utanför radikalen är koefficienter och numren under den kallar vi för rottal. Så här förenklar du termerna:

6√50 = 6√(25 x 2) = (6 x 5)√2 = 30√2. Du löste upp "50" till "25 x 2" och placerade sedan "5" utanför roten (roten av "25"), varefter "2" förblir under radikalen. Sedan multiplicerar du `5` med `6`, talet som redan var utanför radikalen, och du får 30 som den nya koefficienten.
2√8 = 2√(4 x 2) = (2 x 2)√2 = 4√2. Här har du räknat in `8` till `4 x 2` och sedan subtraherat kvadratroten ur 4 så att du står kvar med `2` utanför radikalen och en `2` under radikalen. Sedan multiplicerar du `2` med `2`, talet som redan var utanför radikalen, och du får 4 som den nya koefficienten.
5√12 = 5√(4 x 3) = (5 x 2)√3 = 10√3. Här har du räknat in "12" till "4 x 3" och sedan subtraherat kvadratroten ur 4 så att du står kvar med "2" utanför radikalen och en "3" under radikalen. Sedan multiplicerar du `2` med `5`, talet som redan var utanför radikalen, och du får 10 som den nya koefficienten.

Bild med titeln Lägg till och subtrahera kvadratrötter Steg 2

2. Ringa in alla termer med motsvarande rotnummer. När du har förenklat rotnumren för de givna termerna, har du följande ekvation kvar: 30√2 - 4√2 + 10√3. Eftersom du bara kan lägga till eller subtrahera liknande rötter, måste du ringa in dessa termer med samma rot, i det här exemplet: 30√2 och 4√2. Du kan jämföra detta med att addera eller subtrahera bråk, där du bara kan addera eller subtrahera termerna om nämnarna är lika.

Bild med titeln Lägg till och subtrahera kvadratrötter Steg 3

3. Om du arbetar med en längre ekvation och det finns flera par av matchande rottal, kan du ringa in det första paret, stryka under det andra, det tredje med asterisk och så vidare. Genom att ordna liknande termer blir det lättare för dig att visualisera lösningen.

Bild med titeln Lägg till och subtrahera kvadratrötter Steg 4

4. Beräkna summan av koefficienterna för termerna med lika rötter. Allt du behöver göra nu är att beräkna summan av koefficienterna för termerna med lika rötter, och ignorera de andra termerna i ekvationen. Rottalen förblir oförändrade. Tanken är att du anger hur många av den typen av rotnummer det finns totalt. De felaktiga villkoren kan förbli som de är. Så här gör du:

30√2 - 4√2 + 10√3 =

(30 - 4)√2 + 10√3 =

26√2 + 10√3

Del 2 av 2: Mer träning

Bild med titeln Lägg till och subtrahera kvadratrötter Steg 5

1. Gör exempel 1. I det här exemplet lägger du till följande kvadratrötter: √(45) + 4√5. Du måste göra följande:

Förenkla (45). Först kan du lossa den så här √(9 x 5).
Sedan tar du kvadratroten ur nio och du får `3`, som du sedan placerar utanför kvadratroten. Så, √(45) = 3√5.
Lägg nu till koefficienterna för de två termerna med matchande rötter för att få ditt svar. 3√5 + 4√5 = 7√5

Bild med titeln Lägg till och subtrahera kvadratrötter Steg 6

2. Gör exempel 2. Följande exempel är denna uppgift: 6√(40) - 3√(10) + √5. Du måste göra följande för att fixa detta:

Förenkla 6√(40). Först kan du lösa upp "40" till "4 x 10", och du får 6√(40) = 6√(4×10).

Sedan beräknar du `2` från kvadraten `4`, och du multiplicerar detta med den aktuella koefficienten. Nu har du 6√(4×10) = (6 x 2)√10.

Multiplicera de två koefficienterna och du får 12√10`.`

Uppgiften lyder nu som följer: 12√10 - 3√(10) + √5. Eftersom de två första termerna har samma rot kan du subtrahera den andra termen från den första och lämna den tredje som den är.

du älskar nu (12-3)√10 + √5 om, vilket kan förenklas till 9√10 + √5.

3. Gör exempel 3. Detta exempel går så här: 9√5 -2√3 - 4√5. Ingen av rötterna innehåller en kvadrat, så ingen förenkling är möjlig. De första och tredje termerna har lika rötter, så deras koefficienter kan subtraheras (9 - 4). Rotnumret förblir detsamma. De återstående termerna är inte lika, så problemet kan förenklas till5√5 - 2√3`.`

Bild med titeln Lägg till och subtrahera kvadratrötter Steg 7

Bild med titeln Lägg till och subtrahera kvadratrötter Steg 8

4. Gör exempel 4. Anta att du har att göra med följande problem: √9 + √4 - 3√2 Du måste nu göra följande:

Eftersom √9 lika √(3x3), kan du förenkla detta: √9 blir 3.

Eftersom √4 lika √(2x2), kan du förenkla detta: √4 blir 2.

Nu summan 3 + 2 = 5.

Eftersom 5 och 3√2 är inte lika villkor, det finns inget mer att göra nu. Ditt sista svar är 5 - 3√2.

Bild med titeln Lägg till och subtrahera kvadratrötter Steg 9

5. Gör exempel 5. Låt oss försöka ta summan av kvadratrötter som ingår i ett bråk. Precis som ett vanligt bråk kan du nu bara beräkna summan av bråk med samma täljare eller nämnare. Låt oss säga att du arbetar med det här problemet: (√2)/4 + (√2)/2, Gör nu följande:

Se till att dessa termer har samma nämnare. Den minsta gemensamma nämnaren eller nämnaren som är delbar med både "4" och "2" är "4".

Så för att göra den andra termen ((√2)/2) med en nämnare 4, måste du multiplicera både täljaren och nämnaren med 2/2. (√2)/2 x 2/2 = (2√2)/4.

Lägg till nämnaren för bråken samtidigt som nämnaren är densamma. Gör bara som du skulle om du adderade bråk. (√2)/4 + (2√2)/4 = 3√2)/4`.`