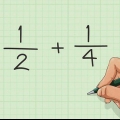Den reciproka 3/4 är 4/3. Den reciproka 7/5 är 5/7. Den reciproka 1/2 är 2/1 och därför 2. 
Lämna räknaren oförändrad. Gör divisionstecknet till en multiplikation. Gör inversen av den andra fraktionen. Multiplicera täljarna för de två bråken. Resultatet blir räknaren för ditt svar. Multiplicera de två bråkens nämnare. Resultatet blir nämnaren för ditt svar. Förenkla bråket. 
1/3 ÷ 2/5 = blir: 1/3 * __ = Nu roterar vi den andra bråkdelen (2/5). Detta blir då 5/2: 1/3 * 5/2 = Nu multiplicerar vi täljarna för de två bråken, 1*5 = 5. 1/3 * 5/2 = 5/ Nu multiplicerar vi nämnarna för de två bråken, 3*2 = 6. Vi har nu: 1/3 * 5/2 = 5/6 Just denna fraktion kan inte förenklas ytterligare, så vi har nu vårt svar. 



2/3 * 7/3 = __ 

Dela disken först 14 medelst 9.9 går in i 14 en gång, med resten av 5, så du kan skriva detta som: 1 5/9. Du kan sluta nu, för du har hittat svaret! Du kan se att denna bråkdel inte kan förenklas ytterligare, eftersom 9 inte är helt delbart med 5 och eftersom täljaren är ett primtal. 
Dela först täljaren med nämnaren, (24/10 = 2 resterande 4). Skriv svaret som 2 4/10. Men vi kan förenkla denna bråkdel ännu mer! Observera att 4 och 10 båda är jämna tal, så det första steget är att förenkla genom att dividera dem båda med 2.Bråket är nu 2/5. Eftersom nämnaren (5) inte helt passar in i täljaren (2), och även är primtal, vet du att du inte kan förenkla detta bråk ytterligare. Så svaret är: 2 2/5. 
Dela bråk med bråk
Att dividera en bråkdel med en bråkdel kan verka förvirrande till en början, men det är faktiskt väldigt enkelt. Allt du behöver göra är att invertera den nedre eller andra bråkdelen och sedan multiplicera båda bråken! Den här artikeln kommer att visa dig hur du gör detta och kommer att visa dig att det inte borde vara ett problem att dividera bråk med bråk.
Steg
Del 1 av 2: Förstå hur det fungerar

1. Tänk på vad att dividera med bråk betyder.Övningen 2 ÷ 1/2 säger samma sak som: ”Hur många gånger går ½ i 2?”Svaret är 4, eftersom du kan dela 2 i 4 halva delar.
- Försök också tänka på detta problem i termer av glas vatten: Hur många halva glas vatten är det i 2 glas vatten?? Du kan lösa detta genom att hälla upp 2 halva glas vatten i ett annat glas, så att du till slut har 2 fulla glas vatten: 2 halva/1 glas * 2 glas = 4 halva glas.
- Det betyder att om du dividerar ett tal med ett tal mellan 0 och 1 kommer svaret alltid att vara större än det talet! Detta gäller oavsett om du dividerar ett heltal eller en bråkdel med en annan bråkdel.

2. Division är motsatsen till multiplikation.Så du kan också tänka på att dividera med en bråkdel som att multiplicera med det reciproka av bråket.Inversen av ett bråk är vad det säger, helt enkelt byta täljare och nämnare. Om ett ögonblick ska vi dividera bråk med bråk genom att multiplicera med nämnarens reciproka, men för nu ska vi titta på några inverser av bråk:

3. Kom ihåg följande steg för att dividera en bråkdel med en annan bråkdel.Här är stegen i ordning:

4. Arbeta igenom dessa steg i exemplet 1/3 ÷ 2/5.Vi lämnar täljaren (det första bråket) oförändrad och ändrar divisionstecknet till ett tidtecken:

5. Försök komma ihåg följande:"Att dividera med ett bråk är detsamma som att multiplicera med det reciproka."
Del 2 av 2: Dividera bråk med bråk - exempel

1. Börja med ett exempelproblem. Anta att vi har uppgiften 2/3 3/7. Frågan här är hur ofta 3/7 passar in i 2/3. Få inte panik; det är inte så svårt som det låter!

2. Gör divisionstecknet till ett multiplikationstecken. Uppgiften blir nu: 2/3 * __ (vi kommer att fylla i det tomma fältet om ett ögonblick.)

3. Nu bestämmer vi den reciproka av den andra fraktionen.Det betyder att vi vänder 3/7 så att täljaren blir 3 och nämnaren blir 7.Den reciproka 3/7 är 7/3.Nu skriver vi ner det nya problemet:

4. Multiplicera bråken.Först multiplicerar vi täljarna för de två bråken: 2 * 7 = 14.14 är täljaren för ditt svar.Sedan multiplicerar vi de två bråkens nämnare:3 * 3 = 9.9 är nämnaren i ditt svar.Nu vet du det 2/3 * 7/3 = 14/9.

5. Förenkla bråket.I det här fallet, eftersom täljaren för bråket är större än nämnaren, vet vi att bråket är större än 1, och vi måste konvertera det till ett blandat tal.(Ett blandat tal är ett heltal med en bråkdel, till exempel 1 2/3.)

6. Låt oss prova ett annat exempel!Anta att vi har följande problem 4/5 2/6 =.Ändra först divisionstecken till ett multiplikationstecken (4/5 * __ =), hitta sedan den reciproka av 2/6, vilket är 6/2.Nu är uppgiften följande: 4/5 * 6/2 =__.Nu multiplicerar vi täljarna, 4 * 6 = 24, och nämnare 5* 2 = 10.Nu har vi följande:4/5 * 6/2 = 24/10.Förenkla bråket. Eftersom täljaren är större än nämnaren måste vi konvertera detta till ett blandat bråk.

7. Ta reda på mer om att förenkla bråk. Du kanske har lärt dig allt det en gång, men det skadar aldrig att uppdatera all den förlorade kunskapen igen. Olika artiklar kan hittas på internet för att förbättra dessa färdigheter igen.
"Dela bråk med bråk"
Оцените, пожалуйста статью