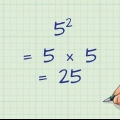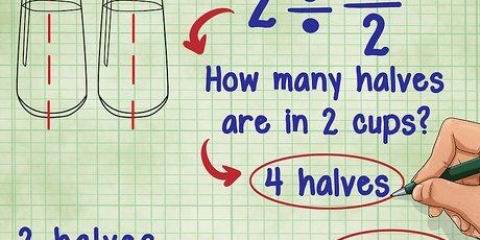Lösa ekvivalenta bråk: 8 steg (med bilder)

Steg
- Metod 1 av 2: Skapa ekvivalenta bråk
- Metod 2 av 2: Lösa ekvivalenta bråk med variabler
Tips
Varningar

Två fraktioner är "likvärdig" om de har samma värde. Till exempel är bråken 1/2 och 2/4 ekvivalenta eftersom 1 över 2 har samma värde som 2 över 4 (0,5 i decimalform). Att veta hur man omvandlar ett bråk till ett annat, men ändå likvärdigt bråk, är en viktig matematik värd att du behöver, från grundläggande algebra till avancerad matematik. Titta på steg 1 för att komma igång!

Steg

Metod 1 av 2: Skapa ekvivalenta bråk

1. Multiplicera täljaren och nämnaren för ett bråk med samma tal för att få ett ekvivalent bråk. Två bråk som är olika, men har ekvivalent per definition, täljare och nämnare som är multiplar av varandra. Med andra ord, multiplicera täljaren och nämnaren för ett bråk med samma tal ger ett ekvivalent bråk. Även om siffrorna i denna nya bråkdel är olika, har den fortfarande samma värde.

Om vi till exempel tar bråket 4/8 och multiplicerar både täljaren och nämnaren med 2, får vi (4×2)/(8×2) = 16/8. Dessa två fraktioner är ekvivalenta.

(4×2)/(8×2) är i huvudsak detsamma som 4/8 × 2/2. Kom ihåg att när vi multiplicerar två bråk så gör vi det så här - täljaren gånger täljaren och nämnaren gånger nämnaren. Observera att 2/2 är lika med 1. Så det är lätt att se varför 4/8 är lika med 8/16 - det andra bråket är det första bråket multiplicerat med 2!

2. Dividera täljaren och nämnaren eller ett bråk med samma tal för att få ett ekvivalent bråk. Liksom multiplikation kan division också användas för att skapa ett nytt bråktal som motsvarar det givna bråket. Dela bara täljaren och nämnaren för ett bråk med samma tal för att få ett ekvivalent bråk. Det finns en varning här - det resulterande bråket måste bestå av heltal i både täljaren och nämnaren för att vara giltig.

Låt oss till exempel ta 4/8 igen. Om vi istället för att multiplicera dividerar både täljaren och nämnaren med 2 får vi (4 2)/(8 ÷ 2) = 2/4. 2 och 4 är båda heltal, så denna ekvivalenta bråkdel är giltig.

Bild med titeln Gör ekvivalenta fraktioner Steg 2

3. Förenkla ditt bråk med den största gemensamma divisorn (GGD). Varje givet bråk har ett oändligt antal ekvivalenta bråk - du kan multiplicera täljaren och nämnaren med vilket heltal som helst, stort eller litet för att få en motsvarande bråkdel. Men den enklaste formen av ett givet bråk är vanligtvis den med de minsta termerna. I så fall är både täljaren och nämnaren så små som möjligt - de kan inte längre delas med något heltal för att göra termen ännu mindre. För att förenkla ett bråk delar vi både täljaren och nämnaren med största gemensamma delaren.

Den största gemensamma divisorn (GGD) för täljaren och nämnaren är det största heltal med vilket både täljare och nämnare är delbara. Så i vårt 4/8-exempel, eftersom 4 är den största divisorn av både 4 och 8, dividerar vi täljaren och nämnaren för vårt bråk med 4 för att få de enklaste termerna. (4 4)/(8 ÷ 4) = 1/2.

Bild med titeln Gör ekvivalenta fraktioner steg 8

4. Om så önskas kan du konvertera blandade tal till oegentliga bråk för att göra omvandlingen enklare. Naturligtvis kommer inte varje bråkdel du stöter på vara lika lätt att förenkla som 4/8. Till exempel blandade nummer (t.ex. 1 3/4, 2 5/8, 5 2/3 osv.) kan göra denna konvertering lite svårare. Om du vill göra en bråkdel av ett blandat tal kan du göra det på två sätt: gör det blandade talet till ett oegentligt bråktal och fortsätt sedan, eller behåll det blandade numret och ge ett blandat nummer som svar.

För att konvertera ett oegentligt bråk, multiplicera det blandade talets heltal med bråkets nämnare och lägg sedan till produkten till täljaren. Till exempel, 1 2/3 = ((1 × 3) + 2)/3 = 5/3. Sedan kan du konvertera den igen om det behövs. Till exempel, 5/3 × 2/2 = 10/6, fortfarande samma som 1 2/3.

Det är dock inte nödvändigt att konvertera en felaktig bråkdel. Vi kan ignorera heltal och bara konvertera bråket och sedan lägga till heltal till det. Till exempel, vid 3 4/16, tittar vi bara på 4/16. 4/16 ÷ 4/4 = 1/4. Så nu lägger vi till heltal igen och får ett nytt blandat tal, 3 1/4.

5. Lägg aldrig till eller subtrahera för att få motsvarande bråk. När du konverterar bråk till motsvarande form är det viktigt att komma ihåg att de enda operationerna du använder är multiplikation och division. Använd aldrig addition eller subtraktion. Multiplikation och division fungerar för att få ekvivalenta bråk eftersom dessa operationer faktiskt är former av talet 1 (2/2, 3/3, etc.).)och ge svar som är lika med bråket du började med. Addition och subtraktion har inte denna förmåga.

Till exempel, ovan fann vi att 4/8 ÷ 4/4 = 1/2 . Om vi istället lagt till 4/4 till detta så hade vi fått ett helt annat svar. 4/8 + 4/4 = 4/8 + 8/8 = 12/8 = 1 1/2 eller 3/2, och ingen av dessa är lika med 4/8.

Metod 2 av 2: Lösa ekvivalenta bråk med variabler

1. Använd korsmultiplikation för att lösa bråkekvivalensproblem. En knepig typ av algebraproblem som hanterar ekvivalenta bråk involverar ekvationer med två bråk, där en eller båda innehåller en variabel. I fall som detta vet vi att dessa bråk är ekvivalenta eftersom de är de enda termerna på vardera sidan av likhetstecknet i en ekvation, men det är inte alltid självklart hur man löser variabeln. Som tur är kan vi multiplicera med korsvis, lösa den här typen av problem utan problem.

Korsmultiplikation är precis vad det låter som - du multiplicerar på ett korsvis över likhetstecknet. Med andra ord multiplicerar du täljaren för ett bråktal med nämnaren för det andra bråket och vice versa. Sedan löser du ekvationen vidare.
Till exempel har vi ekvationen 2/x = 10/13. Korsmultiplicera nu: multiplicera 2 med 13 och 10 med x, och räkna ut ekvationen ytterligare:

2×13 = 26
10 x x = 10 x
10x = 26. Nu räknar vi fram ekvationen vidare. x = 26/10 = 2.6

2. Använd korsmultiplikation på samma sätt som multivariata ekvationer eller variabeluttryck. En av de bästa egenskaperna med korsmultiplikation är att det fungerar ungefär likadant oavsett om du har att göra med två enkla eller komplexa bråk. Till exempel, om båda bråken innehåller variabler kommer ingenting att förändras - du måste bara bli av med dessa variabler. På samma sätt, om täljarna eller nämnarna för din bråkvariabel innehåller uttryck, bara "fortsätta att föröka sig" genom att använda fördelningsegenskapen och lösa som du brukar.

Anta till exempel att vi har ekvationen ((x + 3)/2) = ((x + 1)/4). I det här fallet löser vi detta genom korsmultiplikation:

(x + 3) × 4 = 4x + 12

(x + 1) × 2 = 2x + 2

2x + 2 = 4x + 12

2 = 2x + 12

-10 = 2x

-5 = x

3. Använd tekniker för att lösa polynom. Korsmultiplikation fungerar inte alltid ett resultat som du kan lösa med enkel algebra. Om du har att göra med variabla termer får du snabbt en andragradsekvation eller annat polynom som resultat. I sådana fall använder du till exempel kvadrering och/eller kvadratformeln.

Till exempel tar vi ekvationen ((x +1)/3) = (4/(2x - 2)). Första korset multiplicera:

(x + 1) × (2x - 2) = 2x + 2x -2x - 2 = 2x - 2

4×3 = 12

2x - 2 = 12. Vid det här laget vill vi omvandla detta till en andragradsekvation (ax + bx + c = 0) genom att subtrahera 12 från båda sidor, vilket ger 2x - 14 = 0. Nu använder vi formeln (x = (-b +/- √(b - 4ac))/2a) för att hitta värdet på x:

x = (-b +/- √(b - 4ac))/2a. I vår ekvation är 2x - 14 = 0, a = 2, b = 0 och c = -14.

x = (-0 +/- √(0 - 4(2)(-14))))/2(2)

x = (+/- √( 0 - -112))/2(2)

x = (+/- √(112))/2(2)

x = (+/- 10.58/4)

x = +/- 2.64 Vid denna tidpunkt kontrollerar vi vårt svar genom att ersätta 2,64 och -2,64 i den ursprungliga andragradsekvationen.

Tips

Att konvertera bråk till en ekvivalent form är faktiskt som att multiplicera med ett bråk som 2/2 eller 5/5. Eftersom detta i slutändan är lika med 1, förblir värdet på bråket detsamma.