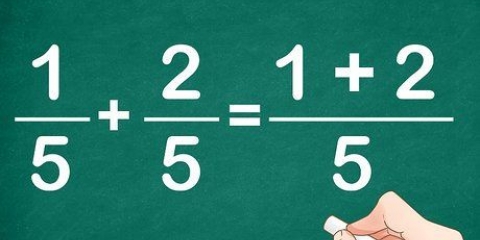I vårt exempel är nämnaren för det staplade bråket (11/15)/(29/70) bråket 29/70. För att hitta inversen vänder vi det och bråket blir 70/29. Observera att om det staplade bråket har ett heltal i nämnaren kan du behandla det som ett bråk och ändå hitta dess invers. Anta till exempel att den staplade bråkdelen var (11/15)/(29), då kan vi definiera nämnaren som 29/1, med den reciproka 1/29. 
I vårt exempel multiplicerar vi 11/15 × 70/29. 70 × 11 = 770 och 15 × 29 = 435. Så är vår nya enkla bråkdel 770/435. 
En gemensam divisor för 770 och 435 är 5. Så om vi dividerar täljaren och nämnaren för vårt bråk med 5 får vi 154/87. 154 och 87 har inga gemensamma faktorer, så vi vet att vi har hittat det slutgiltiga svaret! 

Detta är lättare att förstå med ett exempel. Låt oss försöka förenkla den staplade bråkdelen vi nämnde ovan, (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))). Bråktermerna i denna sammansatta fraktion är (1)/(x+3) och (1)/(x-5). Den gemensamma nämnaren för dessa två bråk är produkten av deras nämnare: (x+3)(x-5). 
I vårt exempel multiplicerar vi den staplade bråkdelen (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))), med ((x+ 3 )(x-5))/((x+3)(x-5)). Vi kommer att behöva multiplicera med täljaren och nämnaren för den staplade bråkdelen, multiplicera varje term med (x+3)(x-5). Låt oss först multiplicera täljaren: (((1)/(x+3)) + x - 10) × (x+3)(x-5) = (((x+3)(x-5)/(x+3)) + x((x+3)(x-5)) - 10((x+3)(x-5)) = (x-5) + (x(x - 2x - 15)) - (10(x - 2x - 15)) = (x-5) + (x - 2x - 15x) - (10x - 20x - 150) = (x-5) + x - 12x + 5x + 150 = x - 12x + 6x + 145 
Nämnaren för vårt staplade bråk, (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))), är x +4 +(( 1)/(x-5)). Vi kommer att multiplicera detta med kgd vi hittade, (x+3)(x-5). (x +4 +((1)/(x - 5))) × (x+3)(x-5) = x((x+3)(x-5)) + 4((x+3)(x-5)) + (1/(x-5))(x+3)(x-5). = x(x - 2x - 15) + 4(x - 2x - 15) + ((x+3)(x-5))/(x-5) = x - 2x - 15x + 4x - 8x - 60 + (x+3) = x + 2x - 23x - 60 + (x+3) = x + 2x - 22x - 57 
Med hjälp av täljaren och nämnaren vi hittade ovan kan vi konstruera ett bråk som är lika med vårt initiala staplade bråk, men som inte innehåller några bråk. Täljaren vi fick var x - 12x + 6x + 145 och nämnaren var x + 2x - 22x - 57, så det nya bråket är: (x - 12x + 6x + 145)/(x + 2x - 22x - 57)
Förenkla staplade bråk
Staplade bråk är de där täljaren, nämnaren eller båda innehåller bråk själva. Av denna anledning kan du också kalla detta `bråk i bråk`. Att förenkla staplade bråk är en process som kan variera från lätt till svår baserat på hur många termer som finns i täljaren och nämnaren, om någon av termerna är variabel och i så fall komplexiteten hos variabeltermerna. Se steg 1 nedan för att komma igång!
Steg
Metod 1 av 2: Förenkla staplade bråk med omvänd multiplikation

1. Om det behövs, förenkla täljaren och nämnaren till några få bråk. Staplade bråk är inte nödvändigtvis svåra att lösa. Faktum är att staplade bråk där täljaren och nämnaren båda innehåller ett enda bråk är vanligtvis ganska lätta att lösa. Så om täljaren eller nämnaren för ditt staplade bråktal (eller båda) innehåller flera bråk eller bråk och heltal, förenkla som du vill för att få ett enstaka bråk i både täljaren och nämnaren. Detta kan kräva den minsta gemensamma multipeln (LCM) för att hitta två eller flera bråk.
- Anta att vi vill förenkla det komplexa bråket (3/5 + 2/15)/(5/7 - 3/10). Först kan vi sedan förenkla både täljaren och nämnaren för vårt komplexa bråk till enstaka bråk.
- För att förenkla täljaren, låt oss ta en LCF på 15, genom att multiplicera 3/5 med 3/3. Vår räknare blir 9/15 + 2/15, vilket är lika med 11/15.
- För att förenkla nämnaren, låt oss ta en lcm på 70, genom att multiplicera 5/7 med 10/10 och 3/10 med 7/7. Vår nämnare kommer att vara 50/70 - 21/70, vilket är lika med 29/70.
- Så vår nya staplade fraktion är (11/15)/(29/70).

2. Vänd på nämnaren och hitta inversen. Per definition, delar från ett nummer till ett annat samma som multiplicera det första talet med ömsesidigt med det andra talet. Nu när vi har erhållit ett staplat bråk med ett enda bråk i både täljaren och nämnaren, kan vi använda denna divisionsegenskap för att förenkla vårt staplade bråktal! Hitta först den reciproka av nämnaren för den staplade bråkdelen. Gör detta genom att "invertera" bråket -- täljaren ersätter nämnaren och vice versa.

3. Multiplicera täljaren för den staplade bråkdelen med nämnarens reciproka. Nu när du har fått den reciproka nämnaren för ditt staplade bråk, multiplicera det med täljaren för att få ett enkelt enkelt bråk! Kom ihåg att för att multiplicera två bråk, multiplicerar vi inte korsvis -- täljaren för det nya bråket är produkten av täljaren av de två gamla, och det gör nämnaren också.

4. Förenkla det nya bråket genom att hitta den största gemensamma divisorn. Vi har nu ett enda, enkelt bråktal, så allt som återstår är att representera det på enklast möjliga termer. Särskild största gemensamma divisor (gcd) av täljaren och nämnaren och dividera båda med detta tal för att förenkla.
Metod 2 av 2: Förenkla staplade bråk med variabeltermer

1. När det är möjligt, använd den inversa multiplikationsmetoden som beskrivs ovan. För att vara tydlig kan nästan alla staplade bråk förenklas genom att reducera täljaren och nämnaren till enstaka bråk och multiplicera täljaren med nämnarens reciproka. Staplade bråkdelar av variabler är inget undantag, men ju mer komplicerade variabeluttrycken i den staplade bråkdelen är, desto svårare och mer tidskrävande är det att utföra omvänd multiplikation. För "enkla" staplade bråk med variabler är multiplikation med inversen ett bra val, men staplade bråk med flera variabeltermer i täljaren och nämnaren kan vara lättare att förenkla med den alternativa metoden som beskrivs nedan.
- Till exempel: (1/x)/(x/6) är lätt att förenkla med invers multiplikation. 1/x × 6/x = `6/x. Det är inte nödvändigt att använda en alternativ metod.
- Bråket (((1)/(x+3)) + x - 10)/(x +4 +((1)/(x - 5))) är dock svårare att förenkla med omvänd multiplikation. Att reducera täljaren och nämnaren för detta staplade bråk till enstaka bråk, multiplicera omvänt och reducera resultatet till de enklaste termerna, är förmodligen en komplicerad process. I det här fallet kan den alternativa metoden nedan vara enklare.

2. Om invers multiplikation är opraktisk, börja med att hitta den minsta gemensamma divisorn av divisionstermerna i den staplade bråkdelen. Det första steget i denna alternativa metod för förenkling är att hitta kgd för alla bråktermer i den staplade bråkdelen -- både i täljaren och i nämnaren. Om en eller flera av bråktermerna har variabler i sina nämnare, är kgd helt enkelt produkten av deras nämnare.

3. Multiplicera täljaren för den staplade bråkdelen med kgd. Därefter måste vi multiplicera termerna i vår staplade bråkdel med kgd av dess bråktermer. Med andra ord, vi multiplicerar hela den staplade bråkdelen med (kgd)/(kgd). Vi kan göra detta helt enkelt för att (kgd)/(kgd) är lika med 1. Multiplicera först täljaren med sig själv.

4. Multiplicera nämnaren för den staplade bråkdelen med kgd som du gjorde med täljaren. Multiplicera den staplade bråkdelen med kgd du hittade genom att gå till nämnaren. Multiplicera varje term med kgd.

5. Skapa en ny, förenklad bråkdel från täljaren och nämnaren du just hittat. Efter att ha multiplicerat ditt bråktal med ditt (kgd)/(kgd)-uttryck och förenklat det genom att stryka ut liknande termer, bör du lämnas med ett enkelt bråktal som inte innehåller bråktermer. Som du kanske har märkt tar nämnarna för dessa bråk ut varandra (genom att multiplicera bråken i den ursprungliga staplade bråkdelen med kgd), och lämnar variabla termer och heltal i täljaren och nämnaren för ditt svar, men inte bråken.
Tips
- Visa varje steg i ditt arbete. Bråk kan vara förvirrande om du vill gå för fort eller försöka få dem ur huvudet.
- Leta efter exempel på staplade bråk på nätet eller i din lärobok. Följ varje steg tills du bemästrar det.
"Förenkla staplade bråk"
Оцените, пожалуйста статью