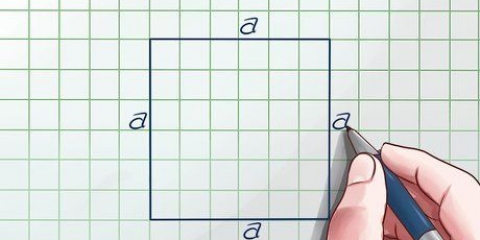
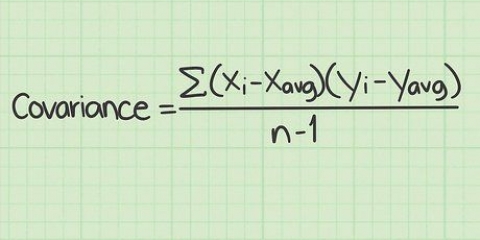Med utgångspunkt från exemplet ovan, lägg märke till att du har fyra värden för X. För att beräkna medelvärdet, räkna alla värden för X och dividera det med 4. Då ser beräkningen ut så här: 



I exemplet ovan har du även fyra värden för y. Lägg till alla dessa värden tillsammans och dividera sedan med 4. Beräkningarna kommer då att se ut så här: 




Med exempeldata kommer dina beräkningar att se ut så här: 





Med exempeldata kommer dina beräkningar att se ut så här: 






Du kanske märker små variationer i formeln, här eller i andra förklaringar. Till exempel kommer vissa att använda den grekiska notationen med rho och sigma, medan andra kommer att använda r och s. Vissa förklaringar kan använda lite olika formler, men de kommer att vara matematiskt likvärdiga med denna. 
Med hjälp av exempeldata kan du mata in data i korrelationskoefficientformeln och beräkna det så här: 
 [
[
 ]
]




Eftersom korrelationskoefficienten är positiv kan man säga att det finns en positiv korrelation mellan x-data och y-data. Det betyder att när x-värdena ökar förväntar du dig att y-värdena också ökar. Eftersom korrelationskoefficienten är mycket nära +1 är x-data och y-data mycket nära relaterade. Om du skulle plotta dessa punkter skulle du se att de är en mycket bra approximation av en rät linje. 

Till exempel: på hemsidan http://ncalculators.com/statistik/korrelationskoefficient-kalkylator.htm hitta en horisontell ruta för att ange x-värden och en andra horisontell ruta för att ange y-värden. Du anger termerna endast separerade med kommatecken. Så den x-datamängd som beräknades tidigare i den här artikeln ska anges som 1,2,4,5. Y-datauppsättningen anges som 1,3,5,7. På en annan sida, http://www.alkohol.com/calculators/statistics/correlation-coefficient/, du kan ange data både horisontellt och vertikalt, så länge du håller ordning på datapunkterna. 


Använd piltangenterna för att flytta markören för att markera kategorin `xStat`. Tryck sedan på "Rensa" och "Enter". Detta bör rensa alla värden i xStat-kolumnen. Använd piltangenterna för att markera kategorin `yStat`. Tryck på "Rensa" och "Enter" för att rensa data från den kolumnen också. 
Fortsätt att ange alla x-värden. När du har angett x-värdena, använd piltangenterna för att flytta till kolumnen yStat och ange y-värdena. När alla data har matats in, tryck på Avsluta för att rensa skärmen och avsluta Stat-menyn. 
Gå in i Stat-funktionen och tryck sedan på Calc-knappen. På TI-86 är detta [2nd][Stat][F1]. Välj linjär regressionsberäkningar. På TI-86 är den [F3], märkt "LinR.` Den grafiska skärmen kommer då att visa raden `LinR _` med en blinkande markör. Du måste nu ange namnen på de två variablerna du vill beräkna. Dessa är xStat och yStat. På TI-86 väljer du listan med namn (`Namn`) genom att trycka på [2nd][List][F3]. Den nedersta raden på din skärm bör nu visa de tillgängliga variablerna. Välj [xStat] (detta är förmodligen knapp F1 eller F2), skriv sedan ett kommatecken och sedan [yStat]. Tryck på Enter för att beräkna data 
 : Detta är den allmänna formeln för en rak linje. Men istället för det välkända `y=mx+b` presenteras detta i omvänd ordning.
: Detta är den allmänna formeln för en rak linje. Men istället för det välkända `y=mx+b` presenteras detta i omvänd ordning. . Detta är värdet på skärningen med y-axeln på den linje som passar bäst.
. Detta är värdet på skärningen med y-axeln på den linje som passar bäst. . Det är den lutning på linan som passar bäst.
. Det är den lutning på linan som passar bäst. . Detta är korrelationskoefficienten.
. Detta är korrelationskoefficienten. . Detta är antalet datapar som används i beräkningen.
. Detta är antalet datapar som används i beräkningen.

Medelvärdet för en variabel indikeras av variabeln med en horisontell linje ovanför. Detta kallas ofta för "x-bar" eller "y-bar" för datamängderna x och y. Alternativt kan medelvärdet betecknas med den grekiska gemena bokstaven μ (mu). Till exempel, för att representera medelvärdet av datapunkter för x, kan du använda μX eller μ(x). Till exempel, om du har en uppsättning av x (1,2,5,6,9,10), så beräknas medelvärdet av dessa data enligt följande: 



Som en symbol uttrycks standardavvikelsen med den gemena bokstaven s eller den grekiska bokstaven σ (sigma). Så standardavvikelsen för x-data skrivs som sX ellerX. 
Till exempel, om du har en uppsättning datapunkter x (1,2,5,6,9,10), betyder ∑x: 1+2+5+6+9+10 = 33
Bestämning av korrelationskoefficienten
Korrelationskoefficienten, betecknad som r eller ρ, är måttet på den linjära korrelationen (sambandet, både i styrka och riktning) mellan två variabler. Det sträcker sig från -1 till +1, med plus- och minustecken för att representera den positiva och negativa korrelationen. Om korrelationskoefficienten är exakt -1, så är förhållandet mellan de två variablerna helt negativt; om korrelationskoefficienten är exakt +1, så är sambandet helt positivt. Två variabler kan ha en positiv korrelation, en negativ korrelation eller ingen korrelation alls. Du kan beräkna korrelationen för hand, med hjälp av några gratis korrelationsräknare tillgängliga online, eller genom att använda de statistiska funktionerna i en bra grafräknare.
Steg
Metod 1 av 4: Beräkna korrelationskoefficienten för hand

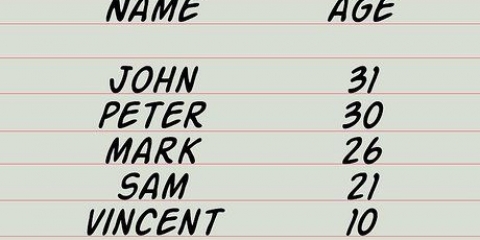
1. Samla in din data först. För att börja beräkna en effektiv korrelation, undersök först dataparen. Det är användbart att lägga dem i ett bord, både vertikalt och horisontellt. Märk varje rad eller kolumn x och y.
- Till exempel: anta att du har fyra datapar för X och y. Tabellen kan då se ut så här:
- x || y
- 1 || 1
- 2 || 3
- 4 || 5
- 5 || 7

2. Beräkna medelvärdet av X. För att beräkna medelvärdet måste du lägga till alla värden för X addera och dividera sedan med antalet värden.




3. Hitta medelvärdet av y. För att få snittet av y För att hitta det, följ samma steg, addera alla värden av y tillsammans och dividera sedan med antalet värden.




4. Bestäm standardavvikelsen för X. När du har dina medel kan du beräkna standardavvikelsen. Använd formeln för detta:







5. Beräkna standardavvikelsen för y. Använd samma grundläggande steg för att hitta standardavvikelsen för y. Du kommer att använda samma formel, med hjälp av datapunkterna för y.






6. Se den grundläggande formeln för att bestämma en korrelationskoefficient. Formeln för att beräkna en korrelationskoefficient använder medel, standardavvikelser och antalet par i en datamängd (representerad av n). Korrelationskoefficienten i sig representeras av den gemena bokstaven r eller den grekiska bokstaven ρ (rho). För den här artikeln kommer vi att använda formeln känd som Pearson-korrelationskoefficienten som visas nedan:


7. Bestäm korrelationskoefficienten. Du har nu medel och standardavvikelser för dina variabler, så du kan gå vidare till korrelationskoefficientformeln. Kom ihåg det n representerar antalet värden du har. Du har redan utarbetat den andra relevanta informationen i stegen ovan.

 [
[
 ]
]




8. Tolka resultatet. För denna datauppsättning är korrelationskoefficienten 0,988. Detta nummer talar om två saker om data. Titta på numrets tecken och numrets storlek.
Metod 2 av 4: Använda onlinekorrelationsräknare

1. Sök på nätet efter korrelationsräknare. Att mäta korrelation är en ganska standardberäkning för statistiker. Beräkningen kan bli mycket tråkig för stora datamängder om den görs för hand. Därför har många källor gjort vanliga korrelationsberäkningar tillgängliga online. Använd valfri sökmotor och ange söktermen "korrelationsräknare".

2. För data i. Läs instruktionerna på webbplatsen noggrant så att du kan ange uppgifterna korrekt. Det är viktigt att dataparen hålls i ordning annars får du ett felaktigt korrelationsresultat. Olika webbplatser använder olika formatering för att ange data.

3. Beräkna resultaten. Dessa beräkningswebbplatser är populära eftersom, i allmänhet, efter att ha angett data, allt du behöver göra är att klicka på knappen "Beräkna" -- resultatet visas automatiskt.
Metod 3 av 4: Använda en grafräknare

1. Ange dina uppgifter. Slå på statistikfunktionen på din grafräknare och välj sedan kommandot `Redigera`.
- Varje miniräknare har lite olika knappkommandon. Den här artikeln innehåller specifika instruktioner för Texas Instruments TI-86.
- Gå in i Stat-funktionen genom att trycka på [2nd]-Stat (ovanför `+`-tangenten) och sedan F2-Edit.

2. Rensa alla gamla sparade data. De flesta miniräknare kommer att behålla de statistiska uppgifterna tills de rensas. För att vara säker på att du inte blandar ihop gamla data med nya data måste du först rensa all tidigare lagrad information.

3. Ange dina datavärden. Använd piltangenterna för att flytta markören till det första utrymmet under rubriken xStat. Skriv in ditt första datavärde och tryck sedan på Enter. Du bör se utrymmet längst ner på skärmen `xStat(1)=__` där ditt värde fyller det tomma utrymmet. När du trycker på Enter kommer data att fylla tabellen, markören flyttas till nästa rad och raden längst ner på skärmen ska nu stå `xStat(2)=__`.

4. Beräkna den linjära regressionsstatistiken. Korrelationskoefficienten är ett mått på hur väl data approximerar en rät linje. En grafräknare med statistiska funktioner kan mycket snabbt beräkna den bästa passningslinjen och korrelationskoefficienten.

5. Tolka resultaten. När du trycker på Enter kommer räknaren omedelbart att beräkna följande information för de uppgifter du angett:
 : Detta är den allmänna formeln för en rak linje. Men istället för det välkända `y=mx+b` presenteras detta i omvänd ordning.
: Detta är den allmänna formeln för en rak linje. Men istället för det välkända `y=mx+b` presenteras detta i omvänd ordning. . Detta är värdet på skärningen med y-axeln på den linje som passar bäst.
. Detta är värdet på skärningen med y-axeln på den linje som passar bäst. . Det är den lutning på linan som passar bäst.
. Det är den lutning på linan som passar bäst. . Detta är korrelationskoefficienten.
. Detta är korrelationskoefficienten. . Detta är antalet datapar som används i beräkningen.
. Detta är antalet datapar som används i beräkningen.Metod 4 av 4: Upprepa grunderna

1. Förstå begreppet korrelation. Korrelation avser det statistiska sambandet mellan två storheter. Korrelationskoefficienten är ett enda tal som du kan beräkna för två uppsättningar datapunkter. Siffran är alltid något mellan -1 och +1, och anger hur nära de två datamängderna är sammankopplade.
- Om du till exempel mätte längden och åldern på barn upp till cirka 12 års ålder, skulle du förvänta dig att hitta en stark positiv korrelation. När barn blir äldre tenderar de att bli längre.
- Ett exempel på en negativ korrelation är att jämföra tiden någon spenderar på att träna golf och den personens golfpoäng. Allt eftersom träningen fortskrider bör poängen sjunka.
- I slutändan skulle du förvänta dig lite korrelation, positiv eller negativ, mellan till exempel en persons skostorlek och deras provbetyg.

2. Beräkna medelvärdet. Det aritmetiska medelvärdet, eller "medelvärdet", för en uppsättning data beräknas genom att addera alla värden för data tillsammans och sedan dividera med antalet värden i uppsättningen. När du vill bestämma korrelationskoefficienten för dina data måste du beräkna medelvärdet av varje uppsättning data.




3. Känna till vikten av standardavvikelsen. I statistiken mäter standardavvikelsen variation, vilket visar spridningen av siffrorna i förhållande till medelvärdet. En grupp av tal med låg standardavvikelse ligger ganska nära varandra. En grupp av tal med hög standardavvikelse är mer spridd.

4. Känn igen summeringsnotationen. Summeringsoperatorn är en av de vanligaste operatorerna i matematik, som representerar en summa av värden. Det representeras av den grekiska versalen, sigma eller ∑.
Tips
- Korrelationskoefficienten kallas ibland för Pearsons produkt-moment korrelationskoefficient, för att hedra Karl Pearson, dess utvecklare.
- I allmänhet representerar en korrelationskoefficient större än 0,8 (positiv eller negativ) en stark korrelation; en korrelationskoefficient lägre än 0,5 (igen positiv eller negativ) representerar en svag korrelationskoefficient.
Varningar
- Korrelation visar att två uppsättningar data på något sätt är sammankopplade. Var dock försiktig så att du inte tolkar detta som ett orsakssamband. Om du till exempel jämför människors skostorlekar och deras längd, kommer du sannolikt att hitta en stark positiv korrelation. Större människor har i allmänhet större fötter. Detta betyder dock inte att det att bli lång kommer att få dina fötter att växa, eller att stora fötter gör dig lång. De bara händer tillsammans.
"Bestämning av korrelationskoefficienten"
Оцените, пожалуйста статью