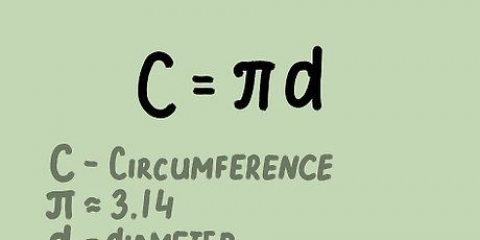Instrucțiuni gratuite pas cu pas 
- Fyll denna kolumn med värdena för punkterna i x-data.
- Fyll denna kolumn med värdena för y-data. Se till att y-värdena är i linje med motsvarande x-värden. I ett kovariansproblem är ordningen på datapunkterna och kopplingen av x och y viktiga.
- Lämna denna kolumn tom i början. Du kommer att fylla den med data efter att du har beräknat ett genomsnitt av x-data.
- Lämna denna kolumn tom i början. Du kommer att fylla den med data efter att du har beräknat ett genomsnitt av y-data.
- Lämna också den sista kolumnen tom. Denna kommer att fyllas i under handläggningen av uppdraget.
Till exempel är den första datapunkten i x-kolumnen 1. Värdet som ska anges på den första raden i kolumnen är: 1 – 4,89 = -3,89. Upprepa denna process för varje datapunkt. Så den andra raden blir: 3 - 4,89 = -1.89. Den tredje raden blir: 2 - 4,89 = -2,89. Fortsätt denna process för alla datapunkter. De nio siffrorna i denna kolumn blir: -3,89, -1,89, -2,89, 0,11, 3,11, 2,11, 7,11, -2,89, -0,89. 
Så för den första raden blir din beräkning: 8 -5,44, = 2,56. Den andra raden blir: 6 – 5,44 = 0,56. Fortsätt subtrahera värdena till slutet av datalistan. När du är klar bör du ha följande nio värden i den här kolumnen: 2,56, 0,56, 3,56, -1,44, -2,44, -2,44, -3,44 , 1,56, 1,56. 
I den första raden av dessa exempeldata visas du beräknade -3,89, och värde 2,56. Produkten av dessa två tal är: -3,89 x 2,56 = -9,96. För den andra raden, multiplicera de två talen: -1,88 x 0,56 = -1,06. Fortsätt att multiplicera rad för rad till slutet av datamängden. När du är klar bör de nio värdena i den här kolumnen vara: -9.96, -1.06, -10.29, -0.16, -7.59, -5.15, -24.46 , -4.51, -1.39. 
Summan av denna exempeldatauppsättning bör läggas till -64,57. Skriv denna summa i utrymmet längst ner i kolumnen. Detta är värdet på täljaren för standardkovariansformeln. 
I detta exempelproblem finns det nio datapar, så n är 9. Därför är värdet på (n-1) lika med 8. 
För denna exempeldatauppsättning är denna beräkning: -64,57/8 = -8,07. 
För att förenkla namngivningen, namnge den tredje kolumnen något som "x skillnad" och den fjärde kolumnen "y skillnad", så länge du kommer ihåg betydelsen av data. Om tabellen börjar i det övre vänstra hörnet av kalkylbladet kommer cell A1 att märkas x, medan de andra etiketterna fortsätter till cell E1. 
X-värdena börjar i cell A2 och fortsätter upp till det antal datapunkter du behöver. Y-värdena börjar i cell B2 och fortsätter upp till det antal datapunkter du behöver. 
Till exempel, om du har 100 datapunkter, kommer cellerna A2 till A101 att fyllas, så i cellen skulle du skriva: = AVERAGE(A2:A101). För y-data, skriv formeln = AVERAGE(B2:B101). Kom ihåg att en formel i Excel börjar med ett `=`-tecken. 
Till exempel är medelvärdet för de 100 datapunkterna i cell A103, så din formel blir: =A2-A103. 
I exemplet med 100 datapunkter går denna formel in i cell E103. Typ: =SUMMA(E2:E102). 
På hemsidan http://ncalculators.com/statistics/covariance-calculator.htm, till exempel finns det en horisontell ruta för att ange x-värdena och en andra horisontell ruta för att ange y-värdena. Du måste ange dina uppgifter separerade med kommatecken. Så, x-datauppsättningen som beräknades tidigare i den här artikeln ska sedan anges som 1,3,2,5,8,7,12,2,4. Y-data som 8,6,9,4,3,3,2,7,7. På en annan sida, https://www.miniräknaren.co/math/Covariance-Calculator-705.html, du kommer att bli ombedd att ange x-data i den första rutan. Data läggs in vertikalt, med en post per rad. Därför ser inlägget på den här webbplatsen ut så här: 1 3 2 5 8 7 12 2 4 
Kovariansen -8,07 för provdatauppsättningen är ganska stor. Observera att uppgifterna sträcker sig från 1 till 12. Så 8 är ett ganska stort antal. Detta indikerar ett ganska starkt samband mellan datamängderna x och y. 
Anta att du kopplar skostorlekar till provbetyg. Eftersom det finns så många faktorer som påverkar en elevs tentamens betyg, kan man förvänta sig ett kovarianspoäng nära 0. Detta indikerar att det nästan inte finns något samband mellan de två värdena. 
För att granska detta igen, läs wikiHow-artiklar om att rita punkter i ett koordinatsystem.
Beräkna kovarians
Kovarians är en statistisk beräkning för att göra förhållandet mellan två uppsättningar data mer transparenta. Antag till exempel att antropologer studerar höjden och vikten av en befolkning inom en viss kultur. För varje person i studien kan längd och vikt representeras med ett datapar (x, y). Dessa värden kan användas i en standardformel för att beräkna kovariansrelationen. Den här artikeln förklarar först beräkningarna för att bestämma kovariansen för en datamängd. Därefter kommer två andra automatiserade sätt att bestämma resultatet att diskuteras.
Steg
Metod 1 av 4: Beräkna kovariansen för hand med hjälp av standardformeln
1. Lär dig standardformeln för kovarians och dess delar. Standardformeln för att beräkna kovariansen är 
. För att använda den här formeln måste du känna till betydelsen av variablerna och symbolerna:
. För att använda den här formeln måste du känna till betydelsen av variablerna och symbolerna: - Denna symbol är den grekiska bokstaven "sigma". I matematiska funktioner innebär detta att man lägger till en serie av det som följer. I den här formeln betyder Σ-tecknet att du beräknar värdena i bråkdelens täljare, sedan adderar dem alla och dividerar sedan summan med nämnaren.
- Du kan läsa denna variabel som `x sub i`. Subskriptet i representerar en räknare. Det betyder att du kommer att göra en beräkning för varje värde på x i din datamängd.
- `avg` indikerar att x(avg) är medelvärdet för alla x datapunkter. Medelvärdet skrivs ibland som ett x med en kort horisontell linje ovanför. I den stilen läser du variabeln som `x-bar`, men det betyder fortfarande medelvärdet av datamängden.
- Du kan läsa denna variabel som `y sub i`. Det nedsänkta i är täljaren. Det betyder att du kommer att göra en beräkning för varje värde på y i din datamängd.
- `avg` indikerar att y(avg) är medelvärdet för alla x datapunkter. Medelvärdet skrivs ibland som ett y med en kort horisontell linje ovanför. I den stilen läser du variabeln som `y-bar`, men det betyder fortfarande medelvärdet av datamängden.
- Denna variabel är antalet element i din datauppsättning. Kom ihåg att i ett kovariansproblem består ett enda "element" av både ett x-värde och ett y-värde. Värdet `n` är antalet par av datapunkter, inte enskilda tal.
2. Konstruera din datatabell. Innan du börjar är det användbart att samla in din data. Skapa en tabell med fem kolumner. Du måste deklarera varje kolumn enligt följande:
- Fyll denna kolumn med värdena för punkterna i x-data. - Fyll denna kolumn med värdena för y-data. Se till att y-värdena är i linje med motsvarande x-värden. I ett kovariansproblem är ordningen på datapunkterna och kopplingen av x och y viktiga. - Lämna denna kolumn tom i början. Du kommer att fylla den med data efter att du har beräknat ett genomsnitt av x-data. - Lämna denna kolumn tom i början. Du kommer att fylla den med data efter att du har beräknat ett genomsnitt av y-data. - Lämna också den sista kolumnen tom. Denna kommer att fyllas i under handläggningen av uppdraget.3. Beräkna medelvärdet av x datapunkter. Denna exempeldatainsamling innehåller 9 nummer. För att hitta medelvärdet, addera dem och dividera summan med 9. Detta ger resultatet 1 + 3 + 2 + 5 + 8 + 7 + 12 + 2 + 4 = 44. När du dividerar detta med 9 får du medelvärdet 4,89. Detta är värdet du kommer att använda som x(avg) för de kommande beräkningarna.
4. Beräkna medelvärdet av y-datapunkterna. Denna y-kolumn måste också bestå av 9 datapunkter som sammanfaller med x datapunkterna. Bestäm medelvärdet av detta. För denna exempeldatauppsättning blir den 8 + 6 + 9 + 4 + 3 + 3 + 2 + 7 + 7 = 49. Dela denna summa med 9 för att få ett genomsnitt på 5,44. Du kommer att använda 5,44 som värdet på y(avg) för de kommande beräkningarna.
5. Beräkna värdena ( X i - X snitt )
. För varje element i x-kolumnen, beräkna skillnaden mellan det numret och medelvärdet. För detta exempelproblem betyder det att man subtraherar 4,89 från varje x-värde. Om den ursprungliga datapunkten är mindre än medelvärdet blir ditt resultat negativt. Om den ursprungliga datapunkten är större än medelvärdet blir resultatet positivt. Se till att hålla reda på vilka värden som är negativa. är: 1 – 4,89 = -3,89.6. Beräkna värdena ( y i - y snitt )
. I den här kolumnen kommer du att göra liknande subtraktioner med hjälp av y-datapunkterna och y-medelvärdet. Om den ursprungliga datapunkten är mindre än medelvärdet blir resultatet negativt. Om den ursprungliga datapunkten är större än medelvärdet kommer ditt resultat att vara positivt. Se till att hålla reda på vilka värden som är negativa.7. Beräkna produkterna för varje datarad. Du fyller i raderna i den sista kolumnen genom att multiplicera siffrorna du beräknade i de två föregående kolumnerna i och . Arbeta dig rad för rad, multiplicera de två talen med deras motsvarande datapunkter. Se upp för eventuella negativa värden på vägen.
och . Arbeta dig rad för rad, multiplicera de två talen med deras motsvarande datapunkter. Se upp för eventuella negativa värden på vägen. du beräknade -3,89, och värde 2,56. Produkten av dessa två tal är: -3,89 x 2,56 = -9,96.8. Hitta summan av värdena i den sista kolumnen. Det är här Σ-symbolen kommer in. Efter att ha gjort alla beräkningar hittills, lägg ihop resultaten. För denna exempeldatauppsättning bör du nu ha nio värden i den sista kolumnen. Lägg ihop dessa nio siffror. Var noga med om en siffra är positiv eller negativ.
9. Beräkna nämnaren för kovariansformeln. Täljaren för standardkovariansformeln är det värde du just beräknade. Nämnaren representeras av (n-1) och är en mindre än antalet par av data i din datamängd.
10. Dividera täljaren med nämnaren. Det sista steget i beräkningen av kovariansen är att dividera täljaren, 
av nämnaren, 
. Kvoten är kovariansen av dina data.
av nämnaren, . Kvoten är kovariansen av dina data.Metod 2 av 4: Beräkna kovarians med hjälp av ett Excel-kalkylblad
1. Lägg märke till vad de repetitiva beräkningarna är. Kovarians är en beräkning som du måste göra för hand några gånger så att du förstår innebörden av resultatet. Men om du rutinmässigt ska använda kovarians för att tolka data, behöver du ett snabbare och automatiserat sätt att få resultaten. Du kanske har märkt vid det här laget att med vår relativt lilla datamängd på bara nio datapar, bestod beräkningarna av två medelvärden, arton separata subtraktioner, nio multiplikationer, en addition och slutligen ytterligare en division. Det är 31 relativt små beräkningar för att hitta lösningen. Längs vägen riskerar du att missa negativa tecken eller kopiera resultatet felaktigt, vilket gör att svaret blir felaktigt.
2. Skapa ett kalkylblad för beräkning av kovariansen. Om du är bekant med Excel (eller något annat beräkningsprogram) kan du enkelt skapa en tabell för att bestämma kovariansen. Märk rubrikerna för de fem kolumnerna precis som i de manuella beräkningarna: x, y, (x(i)-x(avg)), (y(i)-y(avg)) och Product.
3. Fyll i datapunkterna. Skriv in datavärdena i de två kolumnerna x och y. Kom ihåg att ordningen på datapunkterna spelar roll, så du måste matcha varje y med motsvarande värde på x.
4. Bestäm medelvärdet för x- och y-värdena. Excel beräknar genomsnitten åt dig mycket snabbt. I den första tomma cellen under varje kolumn med data skriver du formeln =MEDEL(A2:A___). Fyll den tomma med numret på den cell som motsvarar din senaste datapunkt.
5. Skriv formeln för kolumnen (x(i)-x(avg)). I cell C2 anger du formeln för att beräkna den första subtraktionen. Denna formel blir: =A2-___. Fyll det tomma utrymmet med celladressen som innehåller medelvärdet av x-data.
6. Upprepa formeln för datapunkterna (y(i)-y(avg)). Efter samma exempel kommer det att finnas i cell D2. Formeln blir: =B2-B103.
7. Skriv formeln för kolumnen `Produkt`. I den femte kolumnen måste du i cell E2 skriva in formeln för att beräkna produkten av de två föregående cellerna. Detta blir då: =C2*D2.
8. Kopiera formlerna för att fylla tabellen. Hittills har du bara programmerat de första få datapunkterna i rad 2. Använd musen och markera cellerna C2, D2 och E2. Placera markören på den lilla rutan i det nedre högra hörnet tills ett plustecken visas. Klicka och håll ned musknappen och dra ner musen för att utöka markeringen och fylla hela datatabellen. Detta steg kommer automatiskt att kopiera de tre formlerna från cellerna C2, D2 och E2 till hela tabellen. Tabellen ska automatiskt fyllas med alla beräkningar.
9. Programmera summan av den sista kolumnen. Du behöver summan av artiklarna i kolumnen `Produkt`. I den tomma cellen omedelbart under den sista datapunkten i den kolumnen skriver du formeln: =SUMMA(E2:E___). Fyll den tomma med celladressen för den sista datapunkten.
10. Bestäm kovariansen. Du kan också låta Excel göra den slutliga beräkningen åt dig. Den sista beräkningen i cell E103 i vårt exempel representerar täljaren för kovariansformeln. Direkt under den cellen skriver du formeln: =E103/___. Fyll fältet med antalet datapunkter du har. I vårt exempel är detta 100. Resultatet är kovariansen av dina data.
Metod 3 av 4: Använda online kovarianskalkylatorer
1. Sök på nätet efter kovarianskalkylatorer. Olika skolor, företag eller andra källor har webbplatser som beräknar kovariansvärdena mycket enkelt för dig. Använd sökordet `kovarianskalkylator` i en sökmotor.
2. Ange dina uppgifter. Läs instruktionerna på webbplatsen noggrant för att vara säker på att du anger informationen korrekt. Det är viktigt att dina datapar hålls i ordning, annars blir det genererade resultatet en felaktig kovarians. Webbplatser har olika datainmatningsstilar.
3. Beräkna dina resultat. Det attraktiva med dessa onlineberäkningar är att du efter att ha angett uppgifterna vanligtvis bara behöver klicka på knappen `Beräkna`, varefter resultaten visas automatiskt. De flesta webbplatser ger dig mellanliggande beräkningar av x(avg), y(avg) och n.
Metod 4 av 4: Tolka resultaten av kovariansen
1. Leta efter en positiv eller negativ relation. Kovariansen är ett enda statistiskt tal som anger sambandet mellan en datamängd och en annan. I exemplet som nämns i inledningen mäts längden och vikten. Du kan förvänta dig att när människor växer kommer deras vikt också att öka, vilket leder till en positiv kovarianssyn. Ett annat exempel: Antag att data samlas in som indikerar antalet timmar en person har tränat golf och poängen han eller hon uppnår. I det här fallet förväntar du dig en negativ kovarians, vilket innebär att när antalet träningstimmar ökar kommer golfpoängen att minska. (I golf är en lägre poäng bättre).
- Betrakta exempeldatauppsättningen som beräknats ovan. Den resulterande kovariansen är -8,07. Minustecknet betyder att när x-värdena ökar, tenderar y-värdena att minska. Du kan se att detta är sant genom att titta på några av värdena. Till exempel motsvarar x-värdena för 1 och 2 y-värdena för 7, 8 och 9. X-värdena för 8 och 12 är kopplade till y-värdena för 3 respektive 2 .
2. Tolka storleken på kovariansen. Om kovarianspoängens nummer är stort, antingen ett stort positivt tal eller ett stort negativt tal, så kan du tolka detta som två dataelement som är starkt kopplade, antingen på ett positivt eller negativt sätt.
3. Förstå bristen på en relation. Om ditt resultat är en kovarians lika med eller mycket nära 0, kan du dra slutsatsen att datapunkterna inte har något samband. Det vill säga att en ökning av ett värde kan, men behöver inte leda till en ökning av det andra. De två termerna är sammanlänkade nästan godtyckligt.
4. Se förhållandet grafiskt. För att förstå kovarians visuellt kan du plotta dina datapunkter i en x,y-graf. När du gör det bör du ganska lätt se att punkterna, även om de inte ligger exakt i en rak linje, tenderar att närma sig ett kluster i en diagonal linje från övre vänster till nedre höger. Detta är beskrivningen av en negativ kovarians. Du ser också att värdet på kovariansen är -8,07. Detta är ett ganska stort antal jämfört med datapunkterna. Det höga antalet antyder att kovariansen är ganska stark, vilket kan härledas från den linjära formen på datapunkterna.
Varningar
- Kovarians har begränsad tillämpning i statistik. Det är ofta ett steg mot att beräkna korrelationskoefficienter eller andra begrepp. Var försiktig med alltför djärva tolkningar baserade på en kovarianspoäng.
Оцените, пожалуйста статью
