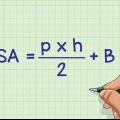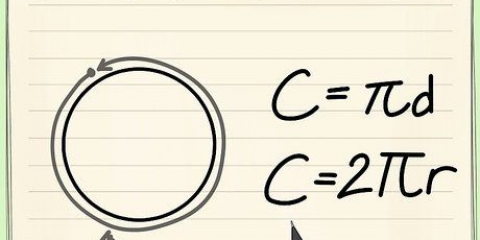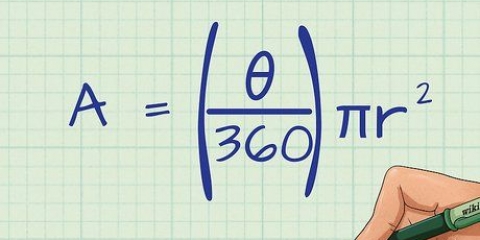Tips för avancerade användare: Om du bara vet volymen av en sfär måste du göra lite mer arbete för att få radien. Dividera volymen med 4π och multiplicera svaret med 3. Slutligen, ta kubroten av detta svar. 

Om vår radie är 5, som ovan, har du kvar 4 x 25 x π, eller 100π. 
100 x = 100 x 3,14 100π = 314 
Det fullständiga svaret för sfären i bilderna är: Area = 314 enheter. De enheter du använder är alltid samma som de som används för att mäta radien. Om radien är i meter blir svaret också i meter. Avancerat tips: Vi kvadrerar enheterna eftersom arean mäter hur många platta rutor som får plats på sfärens yta. Antag att vi mäter övningsproblemet i cm. Det betyder att på en sfär där r=5 skulle vi kunna passa 314 rutor på sfärens yta, om sidorna av varje ruta var 1 cm långa. 
4πr r = 7 4 x x 7 49 x 4 x 196π Svar: Yta = 615,75 cm (kvadratcentimeter). 
Rotation av en cirkel kring dess axel (mitten) producerar en sfär. Tänk på att snurra ett mynt på bordet och hur det ser ut att bilda en sfär. Även om det inte kommer att förklaras här, är det här vår jämförelse kommer ifrån. Tips för avancerade användare: Sfärer har en mindre yta per volym än någon annan form - det betyder att de kan hålla fler saker per yta än någon annan form.
Att bestämma arean av en sfär
Arean av en sfär är antalet kvadratenheter (cm, kvadratcentimeter eller meter - oavsett ditt mått) som täcker utsidan av ett sfäriskt föremål. Ekvationen upptäcktes för tusentals år sedan av den grekiske filosofen och matematikern Aristoteles och relativt enkel (även om dess ursprung inte är det). För att hitta arean av en sfär, använd formeln (4πr), där r är cirkelns radie.
Steg

1. Känna till delarna av ekvationen (Area = 4πr). Denna antika formel är fortfarande det enklaste sättet att bestämma området för en sfär. Med nästan vilken kalkylator som helst kan du fylla i radien för att få arean av din sfär.
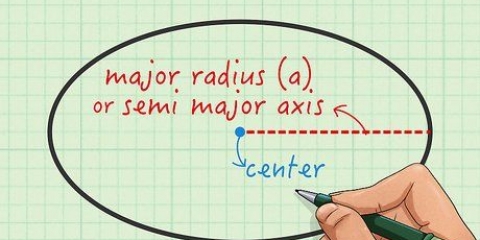
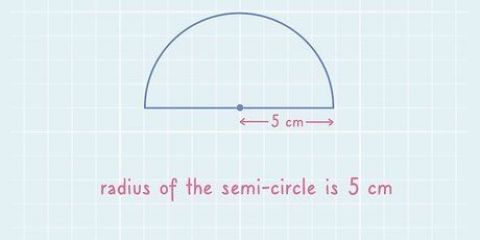
- r eller `radius:` Radien är avståndet från sfärens centrum till sfärens kant.
- π eller `pi:` Detta otroliga tal (motsvarande ungefär 3,14) representerar förhållandet mellan omkretsen och diametern på en cirkel, och är användbar i alla ekvationer som involverar cirklar och sfärer. Det förkortas vanligtvis till π = 3,1416, men det finns ett oändligt antal decimaler.
- 4: Av något komplicerade skäl är arean av en sfär alltid 4 gånger arean av en cirkel med samma radie.

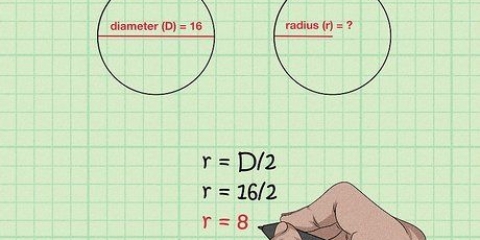
2. Bestäm radien för sfären. Ibland ger problemet dig strålen och andra gånger måste du hitta den själv. För att få diametern på en cirkel, dividera bara diametern med 2 för att få radien. Till exempel: en sfär med en diameter på 10 cm har en radie på 5 cm.

3. Kvadrera radien genom att multiplicera den med sig själv. Du kan göra detta genom manuell multiplikation (5 = 5 x 5 = 25) eller genom att använda din kalkylators kvadratfunktion (ibland kallad "x").

4. Multiplicera detta resultat med 4. Även om du kan multiplicera 4 eller pi först, är det i allmänhet lättare att börja med 4 eftersom det inte finns några decimaler att multiplicera ännu.

5. Multiplicera resultaten med pi (π). Om problemet handlar om ett "exakt värde", skriv symbolen π efter ditt nummer och du är klar. Annars använder du approximationen π=3,14 eller π-knappen på din miniräknare.

6. Glöm inte att skriva dina enheter efter det slutliga svaret. Det ska vara tydligt om ytan på din sfär är till exempel 314 cm eller 314 km. Enheten ska skrivas som "enhet", eftersom detta betecknar area, även känd som "kvadratenheter",

7. Öva med ett exempel. Om radien på en sfär är 7 cm, hur stor är ytan av den sfären??

8. Förstå området. Arean av en sfär är den yta som täcker utsidan av sfären - tänk på det som läder av en fotboll eller jordens yta. Eftersom en sfär är krökt är det mycket svårare att mäta arean av en sfär än av en låda, så vi behöver en ekvation för att bestämma arean.
Tips
- Om radien innehåller en kvadratrot, till exempel 3 √ 5, kom ihåg att inkludera båda koefficientkvadrarna om att kvadratroten. (3 √ 5) blir 9 x 5 = 45.
"Att bestämma arean av en sfär"
Оцените, пожалуйста статью