Beräknar standardfelet

1. Standardavvikelsen. Standardavvikelsen för ett prov anger graden av spridning av siffrorna. Standardavvikelsen för ett prov betecknas vanligtvis med ett s. Den matematiska formeln för standardavvikelsen visas ovan.

2. Befolkningen betyder. Populationsmedelvärdet är medelvärdet av en uppsättning numeriska data som innehåller alla värden för hela gruppen - med andra ord medelvärdet av en komplett uppsättning siffror, snarare än ett urval.

3. Det aritmetiska medelvärdet. Detta är bara ett medelvärde: summan av ett antal värden, dividerat med samma antal värden.

4. Känn igen provmedel. När ett aritmetiskt medelvärde är baserat på en serie observationer som erhållits genom att ta ett urval av en statistisk population, kallas det ett "provmedelvärde"."Detta är medelvärdet av en numerisk uppsättning data där några av värdena inom en grupp finns. Det hänvisas till som:

5. Normalfördelningen. Normalfördelningen, den vanligaste av alla fördelningar, är symmetrisk, med en extremvärde vid medelvärdet av data. Formen på grafen är som en klocka, med lutningen lika på båda sidor om toppen. Femtio procent av fördelningen är till vänster och femtio procent till höger. Fördelningen av en normalfördelning bestäms av standardavvikelsen.

6. Standardformeln. Formeln för standardfelet för ett urvalsmedelvärde ges ovan.

1. Beräkna provmedelvärdet. För att fastställa standardfelet måste du först beräkna standardavvikelsen (eftersom standardavvikelsen, s, är en del av formeln för standardfelet). Börja med att beräkna medelvärdet av provvärdena. Provmedelvärdet uttrycks som det aritmetiska medelvärdet av måtten x1, x2, . . . xn. Detta beräknas med ovanstående formel.

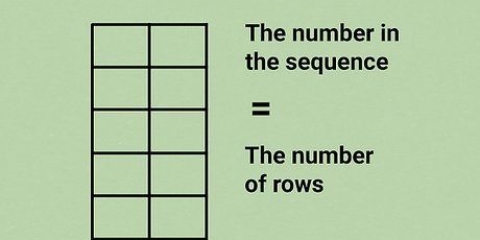
• Anta till exempel att du behöver beräkna standardfelet för ett provmedelvärde för måtten på vikten av fem mynt, enligt listan i tabellen nedan:
  Du skulle sedan beräkna provmedelvärdet genom att ange viktvärdena i formeln, så här:

2. Subtrahera provmedelvärdet från varje mätning och kvadrera detta värde. När du har provmedelvärdet kan du utöka tabellen genom att subtrahera den från varje enskild mätning och sedan kvadrera resultatet.

3. Bestäm den totala avvikelsen för dina avläsningar från provmedelvärdet. Den totala avvikelsen är medelvärdet av den kvadratiska skillnaden från urvalsmedelvärdet. Lägg till alla värden för att bestämma detta.

4. Beräkna medelkvadratavvikelsen för mätningarna från provmedelvärdet. När du vet den totala avvikelsen kan du hitta medelavvikelsen med n -1. Observera att n är lika med antalet mätningar.

5. Bestäm standardavvikelsen. Du har nu alla nödvändiga värden för att använda standardavvikelsens formel.

1. Använd standardavvikelsen för att beräkna standardfelet med standardformeln.

• I exemplet ovan beräknar du standardfelet enligt följande:
  Så standardfelet (standardavvikelsen för provmedelvärdet) är 0,0032031 gram.

Tips

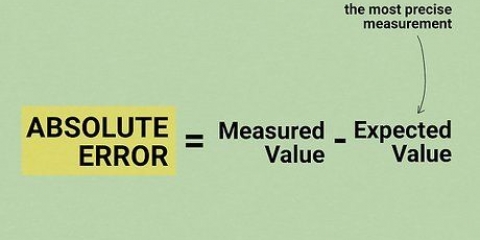
• Standardfelet och standardavvikelsen blandas ofta ihop. Observera att standardfelet är en beskrivning av standardavvikelsen för urvalsfördelningen av ett statistiskt värde, inte fördelningen av de enskilda värdena.
• I vetenskapliga tidskrifter används ibland standardfel och standardavvikelse omväxlande. Ett ±-tecken används för att förena de två avläsningarna.